TEORI PROBABILITAS 1. σ–field dan pengukuran Misalkan Ω

TEORI PROBABILITAS
1. σ–field dan pengukuran
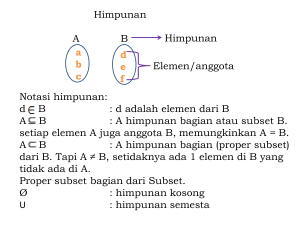
Misalkan Ω adalah elemen dari himpunan. Contoh Ω merupakan himpunan bilangan
dalam suatu interval di bilangan riil yang merupakan hasil dari percobaan random. Dalam
teori probabilitas, Ω disebut sebagai ruang ukuran, sedangkan di teori statistika Ω disebut
ruang sampel. Karena dalam probabilitas dan statistika, Ω biasanya disebut sebagai hasil
yang mungkin dari random eksperimen dalam suatu himpunan.
Pengukuran adalah matematika murni meliputi panjang, luas, atau volume dari himpunan
bagian dalam 1, 2 atau 3 di dimensi ruang Euclid. Dalam pemberian ruang sampel Ω,
pengukuran adalah fungsi himpunan yang didefinisikan dari subset yang di perlukan untuk
memenuhi sifat yang ada pada definisi berikut.
Definisi 1.1
Misalkan F kumpulan subset dari ruang sampel Ω F disebut σ-field jika dan hanya jika
mempunyai sifat berikut :
(i)
himpunan kosong ∅ ∈ F.
(ii)
jika A ∈ F, maka komplemen Ac ∈ F.
(iii) jika Ai ∈ F, i = 1, 2, ..., maka gabungan ∪Ai ∈ F.
Pasangan (Ω,F) terdiri dari himpunan dan σ–field F yang merupakan subset dan
disebut ruang pengukuran. Elemen F disebut himpunan pengukuran dalam teori pengukuran
dan disebut kejadian dalam probabilitas dan statistika.
Karena ∅c = Ω , mengikuti 1 dan 2 pada definisi 1.2 maka Ω Jika F adalah σ–field di Ω
Begitu juga dari 2 dan 3, jika Ai ∈ F, i= 1,2,… dan F adalah σ–field maka irisan ∩Ai ∈ F
dapat di tunjukkan dengan menggunakan hokum deMorgan (∩Ai)c = ∪Aci
. Untuk sebarang Ω yang di berikan ada 2 trivial σ–field yang pertama, kumpulan
yang mengandung 2 elemen ∅ dan Ω Kemungkinan terkecil σ–field dalam Ω yang kedua,
kumpulan semua subset dari Ω yang di sebut himpunan pangkat terbesar σ–field di Ω
Misalkan di berikan nontrivial σ–field. Di berikan A anggota himpunan bagian tak
kosong dari (A ⊂ Ω , A ≠ Ω ) maka {∅,A,Ac,} adalah σ–field. Pada dasarnya σ–field terkecil
mengandung A yang berarti jika F ada σ–field yang mengandung A maka σ–field (1.1)
adalah kumpulan bagian Ω Secara umum σ–field terkecil mengandung C adalah suatu
kumpulan subset dinotasikan σ(C) dan disebut σ–field yang di karenakan C. oleh karena itu
σ–field di (1.1) adalah σ({A}). Catatatn buku σ({A,Ac}), σ({A,}), dan σ({A, ∅}) semua
sama sebagai σ({A}). Tentu jika C sendiri adalah σ–field maka σ(C)=C
Dibilangan R ada σ–field khusus yang akan di gunakan secara langsung. Diberikan C
kumpulan semua interval terbuka di R , maka B = σ(C) di sebut Borel σ–field. Elemen B
disebut himpunan Borel. Borel σ–field Bk di dimensi k sama halnya dengan ruang Euclid rk.
Hal ini dapat di tunjukkan bahwa interval (terbatas atau tak terbatas)himpunan terbuka dan
himpunan tertutup adalah himpunan barel.Kita tunjukkan bilangan riil B = σ(O) dimana O
adalah kumpulan semua himpunan terbuka. Sejenisnya membutuhkan untuk di tunjukkan
bahwa σ(C) ⊂ σ(O) dan σ(O) ⊂ σ(C). karena interval terbuka sama dengan himpunan
terbuka, C ⊂ O dan oleh sebab itu σ(C) ⊂ σ(O). mengapa? Diberikan U adalah himpunan
terbuka. Maka U dapat di tunjukkan sebagai gabungan persamaan dari interval terbuka
terbatas (Royden (1968, p.39)). Oleh karena itu U ∈ σ(C) (definisi 1.1 (iii)) dan O ⊂ σ(C).
dari definisi σ(O), σ(O) ⊂ σ(C). pembuktian terbukti.
Diberikan C ⊂ Rk adalah himpunan borel dan diberikan BC = {C ∩ B : B ∈
Bk}.maka (C, BC) adalah ruang pengukuran dab Bc disebut Borel σ–field di C.
Definisi 1.2
Diberikan (,F) adalah ruang pengukuran. A fungsi himpunan v di definisikan di F di
namakan pengukuran jika dan hanya jika memenuhi sifat berikut :
(i)
0 ≤ ν(A) ≤ ∞ ada A ∈ F.
(ii)
ν(∅) = 0
(iii) jika Ai ∈ F, i = 1, 2, ..., dan Ai saling lepas Ai ∩ Aj = ∅ ada i≠j, maka
~
~
𝑣 (⋃ 𝐴𝑖 ) = ∑ 𝑣(𝐴𝑖 )
𝑖=1
𝑖=1
Ketiga (Ω,F,v) disebut ruang ukuran, jika 𝑉(𝛺) = 1 maka V disebut probabilitas
pengukuran dan biasa dinotasikan oleh P pengganti V yang dioperasikan (𝛺, 𝐹, 𝑃) disebut
ruang probabilitas. Meskipun pengukuran adalah perpanjangan pasang, luas dan volume.
Kadang didapat berupa abstrak. Contoh: diberikan fungsi himpunan
𝑉(𝐴) = ∞
𝑉(𝐴) = 𝐷
Karena pengukuran dapat bernilai
𝐴 ∈ 𝐹, 𝐴 ≠ 0
𝐴=∅
, kita harus mengetahui bagaimana aritmatik dengan
pada buku ini, cukup untuk mengetahui (1) untuk sebarang 𝑥 ∈ 𝑅, ∞ + 𝑥 = ∞ . 𝑥∞ = ∞, jika
𝑥 > 0, 𝑥∞ = −∞, jika 𝑥 < ∞ dan 0∞ = ∞. (2) ∞ + ∞ = ∞ dan (3) ∞𝑎 = ∞ jika sebarang
𝑎 > 0 bagaimana ∞ − ∞ atau ∞⁄∞ tidak terdefinisi.
Jika 𝛺 dapat dihitung berarti ada korespondensi 1-1 diantara 𝛺 dan himpunan semua
bilangan bulat kemudian 1 dapat dipertimbangkan trivial 0 field terdiri dari semua subset dari
𝛺 dan pengukuran memberikan nilai untuk setiap subset di 𝛺. Ketika 𝛺 tidak dapat dihitung,
(e.g., 𝛺 = 𝑅 atau [0,1]), ini tidak mungkin ditetapkan pengukuran yang layak untuk setiap
subset dari 𝛺. Contoh: tidak mungkin ditemukan pengukuran di semua subset di R dan masih
memenuhi sifat 1.3 ini mengapa penting dikenalkan 𝜎 field lebih kecil daripada himpunan
pangkat. Berdasarkan hasil membagi beberapa sifat dasar pengukuran dimanapun kita
memperhubungkan 𝑉(𝐴) secara mutlak diasumsikan 𝐴 ∈ 𝐹.
Dalil 1.1
Diberikan (𝛺, 𝐹, 𝑉) ruang pengukuran
(i)
(Kemonotonan) Jika 𝐴 ⊂ 𝐵 maka 𝑉(𝐴) ≤ 𝑉(𝐵)
(ii)
(Subadditivity) ada persamaan 𝐴1 , 𝐴2 , ….
∞
∞
𝑉 (⋃ 𝐴𝑖 ) ≤ ∑ 𝑉(𝐴𝑖 )
𝑖=1
𝑖=1
(iii) Kekontinuan. Jika 𝐴1 ⊂ 𝐴2 ⊂ 𝐴3 ⊂ ⋯ (𝑎𝑡𝑎𝑢 𝐴1 ⊃ 𝐴2 ⊃ 𝐴3 ⊃ ⋯ 𝑑𝑎𝑛 𝑉(𝐴1 ) < ∞),
maka
𝑉 (lim 𝐴𝑛 ) = lim 𝑉(𝐴𝑛 )
𝑛→∞
𝑛→∞
dimana
∞
∞
lim 𝐴𝑛 = ⋃ 𝐴𝑖 (𝑎𝑡𝑎𝑢 ⋂ 𝐴𝑖 )
𝑛→∞
𝑖=1
𝑖=1
Bukti:
Kita buktikan (i), pembuktian (ii) dan (iii) ditinggalkan sebagai contoh karena 𝐴 ⊂ 𝐵, 𝐵 =
𝐴 ∪ (𝐴𝐶 ∩ 𝐵) dan A dan 𝐴𝐶 ∩ 𝐵 saling lepas dari definisi 1.2 (iii) 𝑉(𝐵) = 𝑉(𝐴) + 𝑉(𝐴𝐶 ∩
𝐵) yang tidak lebih kecil dari 𝑉(𝐴) karena 𝑉(𝐴𝐶 ∩ 𝐵) ≥ 0 oleh definisi 1.2 (i).
Ada korespondensi 1-1 antara himpunan semua pengukuran probabilitas di (R, B) dan
himpunan dari fungsi di R diberikan P probabilitas pengukuran. Fungsi distribusi komulatif
dari P definisi menjadi 𝐹(𝑥) = 𝑃([−∞, 𝑥]), 𝑥 ∈ 𝑅
Dalil 1.2
(i)
Diberikan F ada c.d.f di R, maka
a. 𝐹(−∞) = lim 𝑓(𝑥) = 0
𝑥→−∞
b. 𝐹(∞) = lim 𝑓(𝑥) = 1
𝑥→∞
c. F tidak berkurang 𝐹(𝑥) ≤ 𝐹(𝑦) 𝑗𝑖𝑘𝑎 𝑥 ≤ 𝑦
d. F kontinu kanan
(ii)
lim
𝑦→𝑥, 𝑦>𝑥
𝐹(𝑦) = 𝐹(𝑥)
Andaikan sebuah bilangan real nilai fungsi F di R memenuhi (a.)-(d.) di (i) maka F ada
c.d.f. ukuran probabilitas khusus di (R, B).
Hasil kali kartesius dari himpunan (kumpulan himpunan) 𝑟𝑖 , 𝑖 ∈ 𝐼 = {1, … , 𝑘} (atau
{1,2,,…} didefinisikan sebagai himpunan dari semua (𝑎1 , … , 𝑎𝑘 ) atau (𝑎1 , 𝑎2 , … ) 𝑎1 ∈
𝑟1, , 𝑖 ∈ 𝐼 dan dinotasikan dengan 𝜋𝑖 ∈ 𝐼, 𝑟𝑖 = 𝑟𝑖 𝑥 … 𝑥𝜏𝑘 (𝑎𝑡𝑎𝑢 𝜏1 𝑥𝜏2 ). diberikan (Ω𝑖 , 𝐹𝑖 ), 𝑖𝜖𝐼
dan merupakan ruang pengukuran. Karena 𝜋𝑖 ∈ 𝐼 𝐹2 seharusnya −𝑓𝑖𝑒𝑙𝑑 , 𝜎 (𝜋𝑖 ∈
𝐼, 𝑟𝑖 )𝑑𝑖𝑛𝑜𝑡𝑎𝑠𝑖𝑘𝑎𝑛 𝜋𝑖 ∈ 𝐼 (Ω𝑖 , 𝐹𝑖 ). Sebagai contoh, terdiri (Ω𝑖 , 𝐹𝑖 )=(R,B), i=1,2,….,k. maka
ruang hasil kali Rk dan dapat diperlihatkan 𝜎 − 𝑓𝑖𝑒𝑙𝑑 yang sama dengan Borel 𝜎 − 𝑓𝑖𝑒𝑙𝑑 di
Rk yang mana 𝜎 − 𝑓𝑖𝑒𝑙𝑑 dihasilkan oleh kumpulan semua himpunan terbuka di Rk.
Hasil perkalian dari pengukuran Lebesgue pada dua interval [a1,b1] dan [a2,b2]. Catatan
bahwa [a1,b1] x [a2,b2] adalah sesuatu himpunan yang dapat dihitung dengan definisi hasil
kali 𝜎 field. Sebuah pengukuran V di (𝛺, 𝐹) disebut 𝜎 finite jika hanya jika ada sebuah
persamaan { 𝐴1 , 𝐴2 , … } sebagaimana ∪ 𝐴𝑖 = 𝛺 dan 𝑉(𝐴𝑖 ) < ∞ untuk semua i. Beberapa
ukuran terbatas (seperti pengukuran peluang) adalah pembenaran 𝜎 terbatas. Pengukuran
Lebesgue dalam contoh 1.2 adalah 𝜎 terbatas, tetapi 𝑅 = ∪ 𝐴𝑛 dengan 𝐴𝑛 = (−𝑛, 𝑛), 𝑛 =
1,2, …. Perhitungan ukuran dalam contoh 1.1 adalah 𝜎 terbatas jika hanya jika 𝛺 dapat
dihitung. Pengukuran didefinisikan oleh (1.2), bagaimanapun tidak 𝜎 terbatas.
Dalil 1.3 (Teorema Ukuran Hasil Kali)
Diberikan (𝛺𝑖 , 𝐹𝑖 , 𝑉𝑖 ), 𝑖 = 1, … , 𝑘, sebagai ruang ukuran dengan 𝜎 ukuran terbatas, dimana
𝑘 ≥ 2 adalah bilangan bulat. Kemudian ada sebuah ukuran 𝜎 terbatas yang unik dalam hasil
kali 𝜎 field 𝜎(𝐹1 × … × 𝐹𝑘 ), disebut ukuran hasil kali dan dinotasikan 𝑉1 × … × 𝑉𝑘 , sebagai
berikut:
𝑉1 × … × 𝑉𝑘 (𝐴1 × … × 𝐴𝑘 ) = 𝑉1 (𝐴1 ) … 𝑉𝑘 (𝐴𝑘 )
untuk semua 𝑉𝑖 ∈ 𝐹𝑖 , 𝑖 = 1, … , 𝑘.
Dalam R2 ada ukuran khusus, ukuran hasil kali m x m, untuk m x m ([𝑎1 , 𝑏1 ] ×
[𝑎2 , 𝑏2 ]) sama dengan nilai yang diberikan oleh (1.5). Pengukuran ini disebut Ukuran
Lebesgue di (𝑅 2 , 𝐵 2 ). Pengukuran Lebesgue (𝑅 3 , 𝐵 3 ) adalah m x m x m sama dengan
volume biasa untuk himpunan bagian dari bentuk [𝑎1 , 𝑏1 ] × [𝑎2 , 𝑏2 ] × [𝑎3 , 𝑏3 ]. Pengukuran
Lebesgue di (𝑅 𝑘 , 𝐵 𝑘 ) untuk sembarang bilangan bulat positif k yang didefinisikan.
Konsep dari c.d.f. (Comulatif-Distributif-Function) dapat diperpanjang pada Rk. Diberikan P
merupakan ukuran peluang di (𝑅 𝑘 , 𝐵 𝑘 ). c.d.f. (joint c.d.f.) dari P didefinisikan dengan:
𝐹(𝑥1 , … , 𝑥𝑘 ) = 𝑃((−∞, 𝑥1 ] × … × (−∞, 𝑥𝑘 ]),
𝑥𝑖 ∈ 𝑅
Ada korespondensi satu-satu diantara pengukuran probabilitas dan join c.d.f. di R2.
Beberapa sifat dari sebuah joint c.d.f diberikan pada contoh 10 di (1.6). jika F() adalah
sebuah joint c.d.f. maka Fi(x)= adalah sebuah c.d.f. dan disebut ith marginal c.d.f. secara
jelas, marginal c.d.f. tidak dapat ditentukan oleh joint c.d.f.nya. tetapi sebuah joint c.d.f. tidak
dapat ditentukan dengan k marginal c.d.f. ada suatu kekhususan tetapi merupakan operasi
penting dengan sebuah joint c.d.f. f didefinisikan oleh k marginal c.d.f. Fi didefinisikan :
𝐹(𝑥1 , … , 𝑥𝑘 ) = 𝐹1 (𝑥1 ) … 𝐹𝑘 (𝑥𝑘 ), (𝑥1 , … , 𝑥𝑘 )𝜖𝑅 𝑘
2. Fungsi yang dapat diukur dan distribusi
Sejak dapat berubah-ubah, sering cocok atau sesuai untuk menentukan sebuah fungsi
(mapping) f dari Ω ke ruang yang lebih sederhana (kerap kali). Diberikan B, kemudian
gambaran invers dari B dibawah f yakni:
f−1(B) = {f ∈ B} = {ω ∈ Ω : f(ω) ∈ B}.
Fungsi invers tidak ada untuk didefinisikan.
Pembaca diminta untuk membuktikan sifat berikut:
a. f−1(Bc) = (f−1(B))c for any B ⊂ _;
b. f−1(∪Bi) = ∪f−1(Bi) for any Bi ⊂ _, i = 1, 2, ....
Diberikan C adalah kumpulan himpunan bagian . kita definisikan:
f−1(C) = {f−1(C) : C ∈ C}.
Definisi 1.3.
Diberikan (Ω,F) dan () merupakan ruang yang dapat diukur dan f sebuah fungsi dari Ω untuk.
Fungsi f disebut fungsi yang dapat diukur dari (Ω,F) ke () jika hanya jika. Jika =R dan =B
(Borrel ), maka f disebut Borel yang dapat diukur atau disebut fungsi Borrel pada (Ω,F) (atau
dengan hormat untuk f).
Dalam teori probabilitas, sebuah fungsi yang dapat dihitung disebut elemen acak dan
dinotasikan dengan satu dari X,Y,Z,… jika x dapat dihitung dari (Ω,F) ke (R,B), maka ini
disebut variable acak, jika x dapat dihitung dari (Ω,F) ke (Rk,Bk), maka ini disebut vector-k
acak. Jika X1,..Xk merupakan variable acak didefinisikan pada ruang acak probabilitas umum,
maka vector (X1,..Xk) adalah vector-vektor k acak.(sebagai konvensi notasi, ada vector c
didefinisikan dengan (c∈ Rk,), dimana adalah komponen ith dari c.
Jika f dapat diukur dari (Ω,F) ke (), maka (F-1) adalah sebuah sub field dari f (terbukti). Ini
disebut field yang dihasilkan oleh f dan dinotasikan dengan (f).
Sekarang kita menganggap beberapa contoh fungsi yang dapat dihitung. Jika f adalah
kumpulan semua himpunan bagian dari Ω , maka fungsi f dapat diukur. Diberikan A⊂ Ω.
penunjuk fungsi untuk A didefinisikan sebagai:
Untuk sembarang B c R,
Kemudian σ(IA) adalah lebih kecil σ–field dari pada σ–field F asli. Ini adalah alasan lain
mengapa kita mengenal konsep fungsi yang dapat dihitung dan variable acak, dalam
penjumlahan untuk alasan bahwa ini mudah untuk berhubungan dengan bilangan. Sering kali
σ–field f (seperti himpunan pangkat) terdiri atas banyak himpunan bagian dan kita hanya
tertarik pada beberapa dari mereka.salah satu bisa jika definisi variable acak X dengan σ(X)
terdiri atas himpunan bagian yang sangat penting. Secara umum, σ(X) berada diantara σ–
field trivial {∅ , Ω } dan F, dan berisi lebih banyak himpunan bagian jika X lebih dilengkapi.
Untuk fungsi yang sederhana I, kita telah menunjukkan bahwa σ(IA) mengandung hanya
empat elemen.
Kelas fungsi sederhana dikandung oleh kombinasi linear dari indikasi himpunan yang dapat
dihitung.
𝑘
𝜑(𝜔) = ∑ 𝑎𝑖 𝐼𝐴 , (𝜔),
𝑖=1
Dimana A1,….,Ak adalah himpunan yang dapat dihitung pada dan a1,…,ak adalah bilangan
real. Salah satu dapat ditunjukkan secara langsung bahwa sebuah fungsi adalah fungsi Borel,
tetapi mengikuti dengan segera dari dalil 1.4. diberikan A1,…,Ak merupakan partisi (sekat)
dari Ω . Ai adalah disjoin dan gabungan A1∪….∪Ak= Ω. kemudian fungsi sedrhana
diberikan oleh (1.8) dengan perbedaan secara langsung karakteristik partisi dan σ(ϕ) = σ({A1,
...,Ak}).
Dalil 1-4- diberikan (Ω,F) sebagai ruang pengukuran.
(i)
F adalah Borel jika hanya jika f−1(a,∞) ∈ F untuk semua a anggota R.
(ii)
Jika f dan g adalah Borel, maka f.g dan af+bg, dimana a dan b adalah juga
merupakan bilangan real. f/g adalah Borel dibagi g(ω) ≠0 untuk setiap w anggota .
(iii)
Jika f,f,… adalah Borel, maka supn fn, infn fn, limn fn, dan lim infn fn. Lebih lanjut
himpunan
𝐴 = {𝜔𝜖Ω: lim 𝑓𝑛 (𝜔) 𝑎𝑑𝑎}
𝑛⟶~
Adalah sebuah kejadian dan merupakan fungsi.
Adalah Borel
(iv)
Diperkirakan bahwa f dapat diukur dari (Ω,F) pada (), dan g dapat diukur dari ()
ke (). Kemudian komposisi fungsi dari gof dapat diukur dari (Ω,F) ke ().
Diberikan Ω sebuah himpunan Borel pada Rp. jika f adalah fungsi yang kontinu
(v)
dari Ω ke Rp, maka f dapat diukur.
Contoh:
Misalkan Ω himpunan uncontable. A ={A⊆ Ω ⎸A countable atau Ac cauntable} . Untuk
membuktikan A 𝜎-field harus di tunjukkan bahwa A memenuhi 𝐴1 ∪ 𝐴2 ∈ 𝐴 dan A1, A2,
A3,....Ak-1, maka ⋃𝑘−1
𝑖=1 𝐴𝑘 ∈ 𝐴
Jawab :
1. ∅ ∈ 𝐴 𝑘𝑎𝑟𝑒𝑛𝑎 ∅ 𝑐𝑜𝑢𝑛𝑡𝑎𝑏𝑙𝑒. Ω ∈ 𝐴 karena Ωc = ∅
2. Misalkan A ∈ 𝐴, maka A atau Ac countable. Bila A countable, maka A = (Ac)c
countable, yang berarti
Ac ∈ 𝐴. Bila Ac cauntable, maka dari syarat keanggotaan
A, Ac ∈ 𝐴 .
3. Untuk membuktikan 3 atau 3’ kita menggunakan sifat gabungan countable himpunan
countable adalah countable. Misalkan kita mempunyai barisan himpunan A1,
A2,A3,... dengan Ai ∈ 𝐴. Terdapat dua kemungkinan
Pertama , semua Ai countable, maka dengan menggunakan sifat diatas ⋃∞
𝑛=1 𝐴𝑛
countable.
Ini berarti ⋃∞
𝑛=1 𝐴𝑛 ∈ 𝐴
∞
c
c
Kedua terdapat beberapa Ai dengan Aic countable. Karena (⋃∞
𝑖=1 𝐴𝑖 ) = ⋃𝑖=1 𝐴𝑖
countable maka ⋃∞
𝑖=1 𝐴𝑖 ∈ 𝐴
Contoh:
Misalkan 𝛺 = {a,b,c}, A1={∅, Ω{a},{b,c}} dan A2={∅, Ω,{b}, {a,c}}.
Perhatikan bahwa A1 dan A2 merupakan 𝜎–fields tetapi A1∪A2={∅, Ω,{a},{b},{a,c},{b,c}}
bukan 𝜎 -fields karena {a}∪{b}={a,b} ∉ A1∪A2
Bila 𝛺 countable (berhingga atau terhitung) kita selalu bisa mengambil 2𝛺 sebagai 𝜎-fields.
Akan tetapi, bila 𝛺 countable (takhingga tak terhitung), maka karena alasan teknis (Shao,
1999:4), kita mengambil 𝜎-fields yang “lebih kecil” dari 2𝛺 Berikut beberapa kasus khusus
untuk 𝛺 = 𝑅 = {𝑥| − ∞ < 𝑥 < ∞}
Misalkan
C1 = {[a,b]|a;b∈R,a<b}
C2 = {(a,b)|a;b∈R,a<b}
C3 = {[a,b)|a;b∈R,a<b}
C4 = {(a,b]|a;b∈R,a<b}
Perhatikan bahwa C1,C2,C3,C4 bukan 𝜎-field. Menurut teorema, terdapat 𝜎(𝐶1 ), 𝜎(𝐶2 ),
𝜎(𝐶3 ), 𝜎(𝐶4 ) dan 𝜎(𝐶1 ∪ 𝐶2 ∪ 𝐶3 ∪ 𝐶4 ). Menurut Royden 𝜎(𝐶1 ) = 𝜎(𝐶2 ) = 𝜎(𝐶3 ) =
𝜎(𝐶4 ) = 𝜎(𝐶1 ∪ 𝐶2 ∪ 𝐶3 ∪ 𝐶4 ) dan disebut dengan -field Borel dan untuk selanjutnya
disingkat Borel fields dan diberi notasi 𝔅. Anggota Borel fields disebut himpunan Borel.
Oleh :
Jihan Reni Kholidati (131810101040)
Waqiah (131810101014)
Yora Aziza Rodifa (131810101051)