TERMINOLOGI DALAM STATISTIK

Himpunan istilah mengenai
salah satu pokok bahasan
TERMINOLOGI
DALAM STATISTIK
Populasi : kumpulan dari semua elemen
yang sedang dipelajari.
Contoh:
Jika akan diteliti berapa pengeluaran ratarata Mahasiswa T.LXTRO selama sebulan,
maka Populasinya adalah semua mahasiswa
T.LXTRO
Jika ingin diketahui berapakah rata-rata penghasilan dosen
T.LXTRO sebulan, populasinya adalah ……………………
• Sampel:
Bagian dari polulasi
Dari contoh diatas: bisa 10 mahaiswa T.LXTRO
atau 100 mahasiswa T.LXTRO, atau 25 dosen
T.LXTRO dsb.
Populasi
Sampel 2
Sampel 1
Sampel diadakan bertujuan
untuk:
penghematan waktu
biaya, dan
tenaga.
D
A
T
A
INFORMASI YANG BERSIFAT
NUMERIK (ANGKA),
MEMBANTU UNTUK MEMBUAT KEPUTUSAN YANG
LEBIH INFORMATIF TENTANG SUATU HAL
Dalam statistik hanya bisa diproses dalam bentuk angka atau
sesuatu yang bersifat kuantitatif.
Perasaan tertarik pada sesuatu  skala Likert  skor
TIPE DATA
1. Data kuantitatif
Hasil observasi (pengamatan) atau sesuatu hal yang
bisa dinyatakan dalam angka (numerik)
Contoh: data penjualan barang, jumlah mahasiswa,
dsb.
2. Data kualitatif
Hasil pengamatan yang outputnya hanya bis
dimasukkan dalam suatu katagori.
Contoh: Sikap mahasiswa terhadap cara mengajar
dosennya. Kepadanya akan diberi pilihan, Puas –
Ragu-ragu – Tidak puas
Dalam hal tersebut responden akan hanya memilih satu
pendapat, dan tidak bisa lebih dari satu
Pengukuran Data
Ada 4 jenis data berdasarkan tingkat
pengukuran (level of measurement)
1.Data Nominal
2.Data Ordinal
3.Data Interval
4.Data Rasio
Data Nominal
Data yang diukur dengan skala nominal
adalah data kualitatif yang bersifat setara
(sama) antar data yang satu dengan data
yang lain. Tidak ada urutan diantara data
yang ada.
Contoh:
Kota tempat tinggal, Tempat kuliah,
Gender, Pekerjaan seseorang, dsb.
Data Ordinal
Pada dasarnya sama dengan data nominal, hanya
disini kedudukan data tidak setara, ada urutan
(order) antara data satu dengan data lainnya.
Contoh:
1. Sikap seseorang: sangat setuju, setuju,
cukup setuju, dan tidak setuju
2. Rating acara TV: ****, ***, **, dan *
3. Tingkat kelulusan: A, B, C, dan D
Data Interval
Data yang diukur dengan skala interval
adalah data kuantitatif, mempunyai
perbedaan antara data satu dengan yang
lain, dan perbedaan tersebut jelas terukur
Tidak mempunyai angka nol
Cotoh:
Temperatur Udara, 0o C artinya suhu
udara tidak nol, tidak sama dengan 0oF,
dsb.
Data Rasio
Pada dasarnya sama dengan data interval,
yakni data kuantitatif, perbedaan antara
data bisa diukur dengan jelas
Data Rasio mempunyai angka nol (zero)
yang mutlak.
Hasi pengukuran untuk nilai sesungguhnya
Berat, tinggi badan, dsb
PEMBAGIAN DATA
HIRARKI DATA
DATA
DATA
RAS I O
DATA
KUALITATIF
DATA
NOMINAL
DATA
ORDINAL
DATA
KUANTITATIF
DATA
INTERVAL
DATA
RASI O
DATA
INTERVAL
DATA
ORDINAL
DATA
NOMINAL
PROSES PENGOLAHAN DATA MENJADI
INFORMASI
DATA
STATISTIK DISKRIPTIF
•Diorganisasikan dalam kriteria tertentu
•Diringkas angka-angkanya
•Ditampilkan dalam gambar dan tabel
STATISTIK INDUKTIF
•Uji hipotesa
•Uji hubungan antar variable, dll
INFORMASI / KESIMPULAN
CAKUPAN STATISTIK DESKRIFTIF
PENYAJIAN DATA
Tabel, grafik
RINGKASAN DATA
Central tedency, Variasi data,
Bentuk data
DATA
STATISTIK
Ada dimensi waktu
ANGKA INDEKS
Indeks Laspeyers,
Indeks Fisher, dll
TIME SERIES
Trend,
Dekomposisi data time series
Pembagian data di atas tidak berarti bahwa masing-masing bagian berdiri
sendiri, keempatnya justru saling berkaitan.
Contoh: Deskrifsikan data produksi beras di kota X pada
periode 1990 – 2007.
1. Menyusun data produksi beras dalam sebuah distribusi frekuensi yang
memudahkan pembacaan dan pengertian. Jika perlu data dapat
ditampilkan dalam bentuk tabel (penyajian data)
2. Menghitung rata-rata produksi beras setiap kecamatan atau desa pada
periode tersebut, kemudian mencari standar deviasi produksi beras
dari rata-rata totalnya (karakteristik data)
3. Memperkirakan trend produksi beras di masa mendatang (tahun 2008,
2009, 2010, …)  time rise
TABEL KONTINGENSI/KATAGORI
JENIS KELAMIN, PENDIDIKAN, PEKERJAAN, DSB
MELIPUTI DATA DENGAN PENGUKURAN NOMINAL ATAU ORDINAL
CIRI KHAS DARI DATA INI:
DATA BERBENTUK BILANGAN INTEGER (BULAT)
TIDAK MENGANDUNG DESIMAL
Contoh:
Tabel 1. Pemancar radio di Jawa
Jenis gelombang
Radio
Kota di Jawa
Jakarta
Surabaya
Total
Bandung
Bogor
AM
4
14
5
2
25
FM
34
11
21
3
69
Total
38
25
26
5
94
DISTRIBUSI FREKUENSI
Menyusun dan Mengatur data kuantitatif mentah kedalam beberapa
kelas data yang sama, sehingga setiap kelas bisa menggambarkan
karakteristik data yang ada.
Contoh: Nilai ujian Matakuliah dari 50 mahasiswa pada sebuah PT
62.5
40
17.5
4
80
61.7
45
17.5
90
87
70
40
66
67.5
79.6
71.5
65
80.2
61.8
79.2
80.6
40.3
95.8
5.5
94.3
4
45.9
94
4
97
5
78
39.5
23
78.9
15
79
58.2
25
23
25
85.2
59
24.8
5
98
43
75
23.9
10.5
Skor terendah nilai ujian adalah 0 dan tertinggi 100
Membuat ARRAY (mengurutkan data)
Ascending = dari kecil ke besar
Descending = dari besar ke kecil
Bila data di atas dilakukan pengurutan secara ascending, maka tabel tersebut
menjadi:
No.
NILAI
No.
NILAI
No.
NILAI
No.
NILAI
No.
NILAI
1
4.0 11
23.0 21
43.0 31
67.5 41
80.2
2
4.0 12
23.0 22
45.0 32
70.0 42
80.6
3
4.0 13
23.9 23
45.9 33
71.5 43
85.2
4
5.0 14
24.8 24
58.2 34
75.0 44
87.0
5
5.0 15
25.0 25
59.0 35
78.0 45
90.0
6
5.5 16
25.0 26
61.7 36
78.9 46
94.0
7
10.5 17
39.5 27
61.8 37
79.0 47
94.3
8
15.0 18
40.0 28
62.5 38
79.2 48
95.8
9
17.5 19
40.0 29
65.0 39
79.6 49
97.0
10
17.5 20
40.3 30
66.0 40
80.0 50
98.0
No.
NILAI
No.
NILAI
No.
NILAI
No.
NILAI
No.
NILAI
1
4
21
23
41
45
61
70
81
80.2
2
4
22
23.9
42
45.9
62
70
82
80.6
3
4
23
23.9
43
45.9
63
71.5
83
80.6
4
5
24
24.8
44
58.2
64
71.5
84
85.2
5
5
25
24.8
45
58.2
65
75
85
85.2
6
5.5
26
25
46
59
66
75
86
87
7
5.5
27
25
47
59
67
78
87
87
8
6
28
25
48
61.7
68
78
88
90
9
7
29
25
49
61.7
69
78
89
90
10
10.5
30
39.5
50
61.8
70
78.9
90
90
11
10.5
31
39.5
51
61.8
71
78.9
91
94
12
15
32
40
52
62.5
72
79
92
94
13
15
33
40
53
62.5
73
79
93
94.3
14
17.5
34
40
54
65
74
79.2
94
94.3
15
17.5
35
40
55
65
75
79.2
95
95.8
16
17.5
36
40.3
56
66
76
79.6
96
95.8
17
17.5
37
40.3
57
66
77
79.6
97
97
18
23
38
43
58
67
78
80
98
97
19
23
39
43
59
67.5
79
80
99
98
20
23
40
45
60
67.5
80
80.2
100
98
Coba deskripsikan data tersebut di atas
1. Sebagian besar mahasiswa mendapat nilai
berapa ?
2. Berapa jumlah mahasiswa yang mendapat nilai
antara 40 sampai 60 ?
3. Berapa jumlah mahasiwa yang mendapat nilai
dibawah 50 ?
4. Berapa jumlah mahasiswa yang mendapat nilai
diatas 50 ?
Untuk menjawab pertanyaan-pertanyaan tersebut perlu
dibuat DISTRIBUSI FREKUENSI
(MENGUMPULKAN DAN MENGATUR DATA SECARA NUMERIK)
PROSES PEMBUATAN DISTRIBUSI FREKUENSI
1.
2.
3.
4.
Menentukan jumlah kelas
Menentukan interval kelas
Menyusun Distribusi Frekuensi
Perbaikan distribusi frekuensi (bila
dianggap perlu)
5. Memasukan frekuensi pada distribusi
frekuensi
1.
Menentukan jumlah kelas
H.A. Sturges (1926)  k
= 1+3,322 log n
k = jumlah kelas
n = jumlah data
Untuk contoh nilai mahasiswa diatas:
k = 1+3,322 log 100 = 7.644 dibulatkan 8
Dengan demikian, 100 data nilai mahasiswa akan dibuat
distribusi frekuensi dengan jumlah kelas adalah 8
Catatan: Rumus diatas hanyalah sebuah alternatif, tidak harus
digunakan pada setiap kasus
2.
Menentukan interval kelas
• Rumus
I
= interval kelas
range
= nilai maximum - nilai minimum
k
= jumlah kelas
Dari data diatas interval kelas adalah:
98  4
i
Dibulatkan menjadi 12
8
94

 11,75
8
3. Menyusun Distribusi Frekuensi
k=8
I = 12
Maka tabel distribusi frekuensinya
menjadi
Nilai ujian mahasiswa
Frekuensi
0 - 12
*Karena nilai ujian
12 - 24
adalah 100, pada
tabel hanya sampai
angka 96, untuk itu
kelas harus
ditambah, yakni
dimulai dari angka
24 - 36
36 - 48
48 - 60
60 - 72
72 - 84
84 - 96
96 – 108*
96 - 108
4. Perbaikan Tabel
Nilai ujian
mahasiswa
Frekuensi
Nilai ujian
mahasiswa
4 - 14
3,99 – 13,99
14 - 24
13,99 – 23,99
24- 34
23,99 – 33,99
34 - 44
33,99 – 43,99
44 - 54
43,99 – 53,99
54 - 64
53,99 – 63,99
64 - 74
63,99 – 73,99
74 - 84
73,99 – 83,99
84 - 94
83,99 – 93,99
94 - 104
93,99 – 103,99
Frekuensi
5. Memasukan frekuensi pada distribusi frekuensi
Nilai ujian
mahasiswa
3,99 – 13,99
13,99 – 23,99
23,99 – 33,99
33,99 – 43,99
43,99 – 53,99
53,99 – 63,99
63,99 – 73,99
73,99 – 83,99
83,99 – 93,99
93,99 – 103,99
Frekuensi
11
12
6
10
4
10
11
19
7
10
Latihan 1.
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
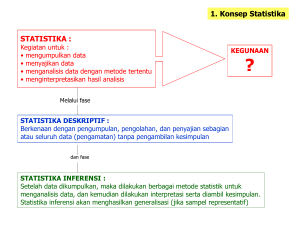
Jelaskan pengertian tentang statistik
Apa yang dimaksud dengan statistik deskriftif dan statistik Inferensial
Jelaskan perbedaan soal 2
Uraikan kegunaan statistik bagi peneliti
Jelaskan apa yang dimaksud dengan distribusi frekuensi
Jelaskan apa yang dimaksud dengan grafik
Sebutkan macam-macam grafik.
Jelaskan perbedaan antara skala pengukuran: Nominal, ordinal, interval dan rasio
Bagaimana hubungan antara skala pengukuran dengan teknik analisis statistik?
Gambarlah grafik untuk data berikut
Jenis gelombang
Radio
Kota di Jawa
Jakarta
Surabaya
Bandung
Bogor
Total
AM
4
14
5
2
25
FM
34
11
21
3
69
Total
38
25
26
5
94
KARAKTERISTIK DATA
(UKURAN-UKURAN STATISTIK)
PADA PRINSIPNYA ADA 3 JENIS KARAKTERISTIK DATA
1. CENTRAL TEDENCY
Ukuran terpusat, menggambarkan keseluruhan data dengan
satu ukuran data tertentu saja.
- rata-rata tinggi badan anak 100 cm  semua tinggi badan
anak 100 cm
2. DISPRESION
Variasi data, seberapa besar data tersebar dari rata-ratanya
- Tinggi badan bervariasi 10 cm, tinggi antara 90 – 110 cm
3. SHAPE OF DATA
Bentuk distribusi data, simetris, menceng kekiri atau menceng kekanan
Tingkat keruncingan: moderat, runcing atau yang lainnya
CENTRAL TEDENCY
Tiga ukuran Central Tedency
1. Mean (rata-rata data),
2. Median (titik tengah data)
3. Modus (frekuensi terbanyak data)
Mean
• Mean = rata-rata = merupakan hasil bagi dari
sejumlah skor dengan banyaknya responden (n).
• Ada beberapa macam mean:
– Rata-rata Hitung: tepat diterapkan untuk skor yang
berderet hitung
– Rata-rata ukur: tepat diterapkan untuk skor yang
berderet ukur
– Rata-rata Harmonik: tepat diterapkan untuk beberapa
kelompok data yang banyak n-nya tidak sama
– Grand mean: tepat diterapkan untuk menghitung ratarata total berdasarkan rata-rata kelompok, menghitung
rata-rata dari beberapa rata-rata.
Mean
RUMUS ; rata-rata hitung sederhana tanpa
frekuensi
n
X 
Xi

i 1
n
Mean
Rata-rata hitung ; untuk data murni/tak berkelompok, deret
hitung
Nilai matematika kelas A: 10 9 8 7 6 5 4 3 2 1  Jumlah = 55; n = 10
Nilai matematika kelas B: 5 6 5 4 8 7 4 6 6 4  Jumlah = 55; n = 10
n
Kelas A
X 
10
 Xi  Xi
i 1
n

n
Kelas B
X 
i 1
10
55

 5,5
10
10
 Xi  Xi
i 1
n

i 1
10
55

 5,5
10
Kelas B lebih homogin dari kelas A
Mean
Rata-rata hitung dengan frekuensi
n
X 

i 1
fi X i
n

i 1
fi
Mean
Contoh rata-rata hitung
X
f
X.f
90
3
270
85
5
425
80
6
480
75
6
450
70
8
560
65
7
455
60
6
360
55
5
275
50
2
100
45
0
0
40
1
40
Jumlah
43
3.415
Rata-rata:
3.415 : 43 = 79,42
Mean
Rata-rata ukur ; data deret ukur, rata-rata geometri
U
n
X1 x X 2 x X 3 x ... X n
Atau
1 n
Log U   Log X i
n i 1
Contoh data deret ukur
Rata-rata ukur:
2 4 8 16 32 64
U  6 2 x 4 x 8 x16 x 32 x 64
Atau
 11,31
1
U  Anti log { ( Log 2  Log 4  Log 8  Log 16  Log 32  Log 64)}
6
1
 anti log { (6,32)}  11,31
6
Mean
Untuk data berkelompok (distribusi frekuensi), rata-rata
ukur dihitung dengan rumus ;
1
log U 
n
n
f
log
Xi
i
i 1
Mean
Rata-rata harmonik
analysis of variance yang
mempunyai jumlah sampel berbeda setiap kelompok
H 
n
n

i 1
1
Xi
2 3 4 5
H 
4
4

i 1
1
Xi
4
 1 1 1 1
345
2
4

 3,12
1,28
Mean
Rata-rata populasi digunakan notasi μ, rata-rata sampel digunakan
notasi X, rata-rata dari beberapa rata-rata GM (Grand Mean) :
Jika n sama untuk masing-masing mean
GM  ( X1  X 2  X 3  ...  X k ): k
k = Banyaknya rata-rata yang akan dicari GM-nya
Jika n tidak sama untuk masing-masing mean
( n1 X 1  n2 X 2  n3 X 3  ...  nk X k )
GM 
n1  n2  n3  ...  nk
Mean
Contoh:
Kelas Rata-rata
n
A
60
10
B
70
10
C
65
10
D
80
10
Kelas Rata-rata
GM  (60  70  65  80 ) : 4
 68,75
n
A
60
10
B
70
8
C
65
7
D
80
15
GM 

(10 x 60  8 x 70  7 x 65  15 x 80 )
10  8  7  15
2815
 70,375
40
Median
•
Kelemahan mean
1.
2.
•
Ada data ekstrim
Kurang tepat untuk data kualitatif
Konsep Median
mengurutkan dan membagi data menjadi dua bagian
dan kemudian menghitung nilai data yang membagi
data menjadi dua bagian tersebut
Median data tak berkelompok
• Menyusun data secara urut, besar kecil atau kecil besar
• Mecari data yang ada ditengah-tengah urutan tadi
dengan rumus:
n 1
Md 
2
• Bila jumlahnya ganjil, menentukan skor mudah  skor
yang terletak ditengah-tengah barisan.
• Bila jumlahnya genap, maka median merupakan ratarata dari dua skor yang paling dekat dengan median
Contoh data berjumlah ganjil
8 5 9 1 7 4 3 2 7  setelah penyusunan, maka
1 2 3 4 5 7 7 8 9
Skor yang membagi distribusi menjadi 2 bagian sama besar adalah
5, sehingga 5 merupakan median
Md 
n 1 9  1

5
2
2
Data yang ke 5
Contoh data berjumlah genap
8 3 4 5 3 7 9 9 8 2  setelah penyusunan, maka
2 3 3 4 5 7 8 8 9 9
n  1 10  1
Md 

 5,5
2
2
(5+7)/2 = 6
Data yang ke 5,5
Median data berkelompok
i
Md  Bb 
(1 / 2 N  f k .b )
fm
Md = Median
B = tepi kelas bawah
fm=frek.kelas interval yang mengandung median
i = interval kelompok
N = jumlah frekuensi
fk.b = frek. Komultif sebelum/di bawah kelas interval yang mengandung median
Contoh …………..
X
f
fk
95 – 99
0
0
90 – 94
1
1
Kelompok yang mengandung median
adalah kelompok yang frek.
Komulatifnya mengandung angka
85 – 89
3
4
½ N  ½ (75) = 37,5.
80 – 84
3
7
75 – 79
8
15
70 – 74
13
28
65 – 69
19
47
Maka kelompok yang mengandung
median adalah 65 – 69 dengan fk = 47
 artinya fk yang dikandung
kelompok ini bergerak dari 28 – 47.
60 – 64
12
59
55 – 59
10
69
40 – 54
4
73
45 – 49
2
75
40 – 44
0
75
i=5
N = 75
Bb = 65, fk.b = 28, fm =19,
maka mediannya:
Md  Bb 
i
(1 / 2 N  f k .b )
fm
5
Md  65 
(1 / 2 x 75  28)  65  2,5  67,5
19
MODUS
Menghitung jumlah data yang paling sering muncul dalam sekelompok data
Dapat dicari dalam distribusi frekwensi
Frekwensi terbanyak.
X
f
5
2
4
6
3
4
2
2
1
1
MODUS terletak pada nilai 4
Catatan: tidak seluruh distribusi frekwensi mempunyai
modus, dan kadang-kadang lebih dari satu
Hubungan mean, median dan
modus
• Data ideal  mean=median=modus
• Moderat  modus = mean – 3(mean-median)
median
modus
mean
median modus
mean
Perbedaan nilai mean dengan modus akan menggambarkan
kondisi penyebaran data yang dihadapi.
Median mempunyai kelebihan daripada mean jika data yang
dianalisis terdapat beberapa skor yang ekstrem, artinya
terdapat perbedaan yang mencolok antara data yang
terendah dengan data yang tertinggi
Bila data yang dihasilkan dari rata-rata tidak mempunyai nilai,
misalnya suatu rata-rata bayi yang dilahirkan pertahun. Dalam
kasus ini kemungkinan rata-rata diperoleh angka pecahan, jadi
tidak mungkin jumlah bayi pecahan.
Dengan demikian penggunaan mean akan lebih baik jika
kondisi seperti ini tidak ada
Distribusi
simetri/normal
Distribusi binominal
Modus
Modus, median, mean
Median
Modus
mean
Tak ada modus
frek,. Masing-masing skor sama
median
modus
median modus
mean
mean
Median
mean
Distribusi skewed negatif
Distribusi skewed positif
Lokasi data
• Kuartil (quartil), membagi sekelompok data
menjadi empat bagian (Q1, Q2, Q3, Q4)
• Desil (decile),  10 bagian (D1…….D10)
• Persentil (percentile),  100 bagian
(P1 …… P100)
Proses penentuan quartile
• Urutkan data dari terkecil ke besar
• Menentukan lokasi data
k (n  1)
Qk 
4
Q = lokasi data yang ke k
K = data urutan ke i yang
akan dicari lokasi datanya
Proses penentuan percentile
• Urutkan data dari terkecil ke besar
• Menentukan lokasi data
nk
Pk 
100
Tugas 2 perorangan
1.
2.
3.
Ada berapa central tedency yang saudara ketahui? Sebutkan dan
jelaskan masing-masing.
Ada berapa macam rata-rata, sebutkan dan jelaskan
Dari hasil pengumpulan jawaban benar 60 responden atas soal multiple
choise sebanyak 20 item sbb:
a. Hitunglah rata-rata
skor yang diperoleh
b. Buatlah tabel
distribusi frekuensi
c. Hitung median
17 12
6 13
12 13 10 13
9 15 11 16
2
11 13 10 20 14
12 17 10 15 12 17
9 18 12 13 12 17
d. Tentukan modus
11 16
e. Buat grafik
12 15 16
4 13
9 14
11 15
8 16 12 16
9 13 18 10 13
0
11 15
7 20 14 14 15 12 13
DISPRESION
VARIABILITAS
1. Range
2. Interquartile Range
(Quartile Deviation)
3. Simpangan Baku
(Standar Deviation, SD)
Range (rentang)
Cara yang paling sedehana dalam mengukur
variasi data.
Semakin besar nilai range berarti semakin
besar perbedaan antara skor terbesar dan
skor terkecil  data makin bervariasi
Range = Data terbesar – Data terkecil
Kelemahannya: tidak dapat menggambarkan bagaimana
variasi skor/data diantara data terbesar dan terkecil (tidak
memperhatikan isi dari data secara keseluruhan
INTERQUARTIL RANGE
Modifikasi range sederhana
Jika pada range sederhana dicari perbedaan antara skor terbesar
dan skor terkecil, maka pada interquartil data yang digunakan
adalah data yang lebih dekat ketitik pusat data
Karena biasanya sifat data,
data bergerombol pada pusat data
Pengukuran menjadi lebih tepat
dalam memperkirakan variasi data
Q = Q3 – Q1
Catatan: Kedua cara diatas merupakan perhitungan variabilitas yang masih kasar
 disarankan tidak dipergunakan secara mandiri
SIMPANGAN BAKU (STANDAR DEVIATION)
Merupakan rata-rata penyimpangan setiap skor dengan rata-rata skornya
Langkah-langkah dalam perhitungan simpangan baku sampel (Sd)
1. Hitung rata-rata skor
2. Hitung perbedaan masing-masing skor dengan rata-rata skor
3. Selisih masing-masing skor dengan rata-rata dikuadratkan dan
dijumlahkan.
4. Hasil penjumlahannya dibagi dengan n-1, hasil perhitungan ini disebut
dengan variance.
5. Akar dari variance adalah Sd
Variance
Sd 
2
(
X

X
)

n 1
2
SIMPANGAN BAKU
Sd  Sd
2
Sd 
2
(
X

X
)

n 1
2
Contoh
1 2 3 4 5
X  15 / 5  3
(X - X )2
X
X- X
1
-2
4
2
-1
1
3
0
0
4
1
1
5
2
4
15
0
10
Dasar Teori Peluang
• Ruang Sampel
• Kejadian dan Operasinya
• Menghitung Titik Sampel :
– Permutasi
– Kombinasi
Ruang sampel
• Kumpulan dari semua hasil
dari percobaan statistik,
dinyatakan dengan notasi S
• Contoh :
Percobaan pelemparan mata
uang
Kejadian
• Dari setiap percobaan kita mungkin ingin mengetahui
munculnya elemen-elemen dari ruang sampel yang
mempunyai ciri tertentu.
Sekelompok titik sampel itu membentuk
himpunan bagian dari S
• Contoh : Percobaan pelemparan 3 koin
Operasi dengan kejadian
• Definisi 1 :
Irisan dua kejadian A dan B, dinyatakan dengan
lambang A B ialah kejadian yang unsurnya
termasuk A dan B.
Gambar diagram Venn
Contoh : Tentukan irisan antara A = {1,2,3,4,5} dan B ={2,4,6,8}
Definisi 2
Dua kejadian A dan B saling terpisah bila
AB=0
• Contoh : Sebuah dadu dilantunkan.
A menyatakan kejadian bahwa
bilangan genap muncul di sebelah atas
dan B kejadian bahwa bilangan ganjil
yang muncul di sebelah atas.
Definisi 3
• Gabungan dua kejadian A dan B,
dinyatakan dengan lambang A B ialah
kejadian yang mengandung semua unsur
yang termasuk A dan B atau keduanya.
• Contoh : Tentukan gabungan dari kejadian
A = {1,2,3,4,5} dengan B = {2,4,6,8}
Definisi 4
• Komplemen suatu kejadian A terhadap S ialah
himpunan semua unsur S yang tidak termasuk A.
Komplemen A dinyatakan dengan lambang A'.
• Contoh :
Q menyatakan kejadian bahwa seorang
karyawan yang dipilih secara acak dari suatu
pabrik adalah seorang perokok. Nyatakan
kejadian komplemen Q ?
Menghitung Titik Sampel
• Teorema 1 :
Bila suatu operasi dapat dilakukan dengan
n1cara, bila untuk tiap cara ini operasi kedua
dapat dikerjakan dengan n2 cara, maka
kedua operasi itu dapat dikerjakan bersamasama dengan n1n2 cara.
• Contoh :
Banyaknya titik sampel dalam ruang sampel
sepasang dadu dilantunkan satu kali.
Teorema 2
• Bila suatu operasi dapat dikerjakan dengan n1
cara, dan bila untuk setiap cara ini operasi kedua
dapat dikerjakan dengan n2 cara , dan bila untuk
setiap kedua cara operasi tersebuat operasi ketiga
dapat dikerjakan dengan n3 cara, dan seterusnya,
maka deretan k operasi dapat dikerjakan dengan
n1n2…nk cara.
• Contoh :
Berapa macam hidangan dapat disajikan jika masingmasing hidangan dapat terdiri dari sop, nasi goreng,
bakmi, dan soto bila tersedia 4 macam soto, 3 macam
nasi goreng, 5 macam bakmi, dan 4 macam soto.
Definisi 5
• Suatu permutasi ialah suatu susunan
urutan yang dapat dibentuk dari suatu
kumpulan benda yang diambil
sebagian atau seluruhnya.
• Contoh : Ambil tiga huruf a, b dan c.
Teorema 3
• Banyak permutasi n benda yang
berlainan adalah n!
• Contoh :
Permutasi empat huruf a,b,c, dan d
adalah 4!=24
Teorema 4
• Banyak permutasi n benda berlainan bila diambil r
sekaligus adalah
• Contoh :
Dari 20 lotere, dua diambil untuk hadiah
pertama dan kedua. Hitunglah banyak
titik sampel dalam ruang S.
Teorema 5
• Banyak permutasi n benda berlainan
yang disusun melingkar adalah (n-1)!
• Contoh :
Dalam suatu permainan bridge ada
empat pemain duduk melingkar. Berapa
susunan duduk yang berlainan dalam
permainan tersebut?
Teorema 6
• Banyak permutasi yang berlainan dari n
benda bila n1 diantaranya berjenis pertama,
n2berjenis kedua,…, nk berjenis ke k adalah
• Contoh :
Suatu pohon natal dihias dengan 9 bola lampu
yang dirangkai seri. Ada berapa cara menyusun 9
bola lampu itu bila tiga diantaranya berwarna
merah, empat kuning dan dua biru?
Teorema 7
• Banyaknya cara menyekat n benda dalam r sel,
masing-masing berisi n1 elemen dalam sel pertama,
n2 dalam sel ke dua dst, adalah
• Contoh :
Berapa banyak cara untuk menampung tujuh
petinju dalam tiga kamar hotel, bila satu kamar
bertempat tidur tiga sedangkan dua lainnya
mempunyai dua tempat tidur ?
Teorema 8
• Jumlah kombinasi dari n benda yang berlainan
bila diambil sebanyak r adalah :
• Contoh :
Bila ada empat kimiawan dan tiga fisikawan,
carilah banyaknya panitia tiga orang yang dapat
dibuat beranggotakan dua kimiawan dan satu
fisikawan.
MENGAWALI SPSS 10.0 FOR WINDOWS
Langkah yang harus dijalankan pertama kali untuk
membuka program adalah sbb:
Klik spss : dialog awal
Klik
Muncul Tampilan utama SPSS
Menu bar
Tool bar
Sel
Pendefinisian
variabel
Nama
variabel
Nama variabel, klik variable vew muncul sbb:
DATA EDITOR
Windows ini merupakan tampilan default dari spss, secara otomatis terbuka
setelah ada tampilan membuka file, sprgbrk:
Windows data editor merupakan menu utama :
• File, Berisi fasilitas yang berhubungan dengan pengelolaan atau
manajemen data dan file seperti terlihat dalam tampilan gambar berikut:
•
Edit: Menu ini berkaiatan dengan operasi/perbaikan ataupun perubahan nilai
data, sekaligus dapat digunakan untuk mengatur setting pada sub menu
Options seperti terlihat pada gambar berikut:
View: digunakan untuk mengatur tools bar, spt tampilan berikut:
Data: digunakan untuk manajemen dan pengelolaan data, spt gbb:
Transform, digunakan untuk memanipulasi data
Analyze, digunakan untukmmenganalisa data
Graph, untuk memvisualkan data
• Utilities,
• Windows, mengatur ukuran jendela
• Help, bantuan informasi yang berkaitan
dgn SPSS
OUTPUT WINDOW
Keluaran dari suatu proses analisa data  SPSS
Viewer
Pada output window memliki menu yang hampir sama dengan menu pada
data editor, tetapi mempunyai tambahan pada menu Insert dan format.
Insert, untuk menambahkan judul, teks, judul halaman, grafik, ataupun obyek
Format, untuk mengatur tampilan huruf, rata kiri, tengah-tengah, dsb
Memasukan data kedalam SPSS
ada 2 cara :
1.
Masukan data terlebih dahulu dilanjutkan dengan
pendefinisian nama variabel
Masukan data kedalam sel sptgbb:
Nama variabel
Data dalam sel
Untuk mengubah nama variabel dengan cara meng-klik
variabel view
Hasil perubahannya:
2. Pendefinisian nama variabel terlebih dahulu dilanjutkan dengan Masukan data
Hasil