14 BAB 4 ΜΕΤΟDOLOGI PEMECAHAN MASALAH DAN

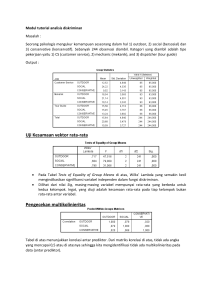
14
BAB 4
ΜΕΤΟDOLOGI PEMECAHAN MASALAH DAN PERANCANGAN
4.1 Model Rumusan Masalah dan Pengambilan Keputusan
Pada penelitian yang dilakukan oleh penulis, bentuk kontur tengkorak
dianggap sebagai sebuah gelombang cyclic. Dengan menerapkan teori Fourier,
gelombang cyclic kemudian dipisahkan menjadi fungsi-fungsi trigonometri. Garis
kontur bentuk dahi dianggap sebagai suatu jumlah keseluruhan dari banyak titik pada
suatu koordinat kartesius. Titik asal berada pada titik nasion, sumbu X berada pada
garis yang menghubungkan titik nasion dan titik bregma. Sedangkan sumbu Y
berada pada garis yang berawal di titik nasion. Gambar 4.1 memperlihatkan letak
titik nasion, titik bregma, dan sumbu-sumbu koordinat.
Gambar 4.1 – Sumbu koordinat tempat garis kontur dahi
15
Gambar 4.2 – titik-titik sampel (x0 dan y0) hingga (x31 dan y31)
Tanpa merubah bentuk dahi, diambil 32 titik sampel (X0, Y0) sampai (X31,
Y31), pada suatu interval yang sama (lihat Gambar 4.2) sehingga gelombang cyclic
yang diekpresikan sebagai urutan dari 32 titik dideskripsikan sebagai basis analisis
Fourier dengan menggunakan persamaan (Pers) 1 atau Pers. 2.
(1)
16
⎛ 2πix ⎞ 16
⎛ 2πix ⎞
a 0 + ∑ ai cos⎜
⎟ + ∑ bi sin ⎜
⎟
⎝ 32 ⎠ i =1
⎝ 32 ⎠
i =1
(2)
16
⎡
⎞⎤
⎛ 2πix
+ θi ⎟⎥
a 0 + ∑ ⎢ci sin ⎜
⎝ 32
⎠⎦
i =1 ⎣
Dengan jumlah titik posisi fungsi sama dengan 16 untuk masing-masing
fungsi sinus dan cosinus, Pers 1 akan menghasilkan 33 konstanta, yaitu a0, a1, a2, … ,
a16, dan b1, b2, … , b16. Ke-32 konstanta, a1, a2, … , a16 dan b1, b2, … , b16,
menyatakan bahwa terdapat 32 amplitudo gelombang fungsi trigonometri yang
melalui 32 titik sampel. Jumlah amplitudo sebanyak 32 buah dianggap sudah cukup
banyak bagi suatu fungsi trigonometri.
16
a0 dan c1 sampai dengan c16 disebut amplitudo-amplitudo harmonik, dan
dihitung dengan Pers.3 sampai Pers.6. a0 menunjukan nilai rata-rata dari y1 sampai
y31, dan menunjukan keseluruhan besaran dari dahi. c1 sampai c16 menunjukan
derajat lekukan dari bentuk kontur. Dengan cara ini, pada setiap gelombang
dihasilkan 17 nilai (a0 dan c1 sampai c16). φ1 sampai φ16 disebut sudut fase, namun
pada penelitian yang dilakukan penulis, sudut fase tidak digunakan.
(3)
a0 =
1 31
∑ yj
32 j =1
(4)
ai =
1 31 ⎡
⎛ 2πij ⎞⎤
yj cos⎜
⎟⎥
∑
⎢
32 j =1 ⎣
⎝ 32 ⎠⎦
(i = 1…16)
1 31
(4’) a16 =
∑ [yj cos(πj )]
32 j =1
(5)
bi =
1 31 ⎡
⎛ 2πij ⎞⎤
yj sin ⎜
⎟⎥
∑
⎢
32 j =1 ⎣
⎝ 32 ⎠⎦
(i = 1…16)
(5’) b16 = 0
+ bi 2 )
(i = 1…16)
θι = arctan⎜
⎛ ai ⎞
⎟
⎝ bi ⎠
(i = 1…16)
⎛ ci ⎞
di = ⎜ ⎟ ⋅ 100
⎝ ai ⎠
(i = 1…16)
(6)
ci =
(7)
(8)
(ai
2
Nilai-nilai d yang dihasilkan oleh Pers 8 disebut normalized harmonic amplitudes. Nilai
d dihitung untuk menghindari pengaruh besar tengkorak pada saat menganalisis bentuk
tengkorak.
17
4.2 Teknik Pengumpulan Data dan Penentuan Parameter
Data yang dikumpulkan berupa hasil scanned dari foto rontgen bagian kepala
manusia (cephalometry) yang terdiri dari kasus pada laki-laki maupun perempuan.
Jumlah pengambilan data yang diambil hanyalah sebagian dari elemen anggota
populasi, oleh karena itu cara pengumpulan datanya dapat dikatakan sebagai cara
sampling. Ukuran sampel data yang diambil sebanyak 20 data untuk masing-masing
jenis kelamin, yaitu laki-laki dan perempuan. Karena ini syarat minimum ukuran
sampel yang bisa dikatakan mewakili suatu populasi.
Proses penelitian ini, dimulai dengan menganalisis sampel dengan metode
analisis Fourier, untuk mendapatkan nilai normalized harmonic amplitudes. Data ini
harus diteliti lebih lanjut untuk mendapatkan koefisien fungsi diskriminan linear dan
kemudian diperoleh nilai fungsi diskriminan linear. Proses tersebut menggunakan
Analisis Diskriminan dan Uji statistik T2-Hotteling
4.2.1 Analisis Diskriminan
Pada penelitian yang akan dilakukan oleh penulis, populasi induk yang
akan diuji adalah sejumlah bentuk dahi manusia pada citra cephalometry, yang
terbagi atas 2 kelompok, yaitu populasi laki-laki dan populasi perempuan. Dari
masing-masing populasi diambil secara acak contoh berukuran 20. Dengan
demikian ukuran sampel secara keseluruhan dari populasi laki-laki dan
perempuan adalah 20 + 20 = 40 dengan 16 buah sifat yang didapat dari nilai
normalized harmonic amplitudes.
(9)
⎛ c (i ,k ) ⎞
d (i ,k ) = ⎜
⎟ ⋅ 100
⎝ a (i ,k ) ⎠
18
i = angka suatu titik posisi dari fungsi ( 1..16 )
k = jumlah sampel yang diuji ( 1 .. 40 )
Dalam bentuk catatan matriks dapat dinyatakan sebagai berikut:
Tabel 4.1 Matriks sampel yang diuji
⎡ d (1,1) d (1,2) d (1,3) L d (1,40) ⎤
⎢ d (2,1)
d (2,40) ⎥⎥
O
⎢
⎢ M
⎥
O
M
⎢
⎥
O
M
⎢ M
⎥
⎢⎣d (16,1) d (16,2) d (16,3) L d (16,40)⎥⎦
Dari k sampel yang diamati, dapat diperoleh nilai rata-rata V1, V2, … , V16.
Tabel 4.2 Nilai rata-rata kelompok untuk 16 variabel
Variabel
Laki-laki ( 20 sampel )
Perempuan ( 20 sampel )
V1
∑
d (1,k )
= V (1,1)
k =1 20
d (1,k )
= V (1, 2 )
k = 21 20
V2
d ( 2,k )
= V ( 2,1)
∑
k =1 20
d ( 2,k )
= V ( 2, 2 )
k = 21 20
M
M
M
V16
20
20
d (16,k )
= V (16,1)
∑
20
k =1
20
40
∑
40
∑
d (16,k )
= V (16, 2 )
k = 21 20
40
∑
Tabel 4.3 Matriks rata-rata kelompok Laki-laki
⎡ V (1,1) ⎤
⎢
⎥
V ( 2,1) ⎥
⎢
V1 =
⎢ M ⎥
⎢
⎥
⎣⎢V (16,1) ⎦⎥
19
Tabel 4.4 Matriks rata-rata kelompok Perempuan
⎡ V (1, 2 ) ⎤
⎥
⎢
V ( 2, 2 ) ⎥
⎢
V2 =
⎢ M ⎥
⎥
⎢
⎢⎣V (16, 2 ) ⎥⎦
Berdasarkan matriks pada tabel 4.1, dapat ditentukan matriks ragam-peragam
(variance-covariance), dengan cara menurunkan rumus umum variance (pers. 10)
kedalam rumus yang disesuaikan dengan kasus 2 kelompok (pers. 10’) dan akhirnya
diperoleh rumus untuk penelitian ini (pers.11 dan pers. 12)
⎡ n
2⎤
⎢∑ Xp − X ⎥
p =1
⎦
(10) S 2 = ⎣
(n − 1)
(
)
2
⎡ n
⎛ n
⎞ ⎤
2
n
X
−
Xp
p
⎜∑ ⎟ ⎥
⎢ ∑
⎝ p =1 ⎠ ⎥⎦
⎢⎣ p =1
2
(10’) S =
n(n − 1)
⎡ n
⎞⎤
⎛ n
⎞⎛ n
⎢n∑ X (i , p ) X (q , p ) − ⎜ ∑ X (i , p ) ⎟⎜ ∑ X (q , p ) ⎟⎥
⎝ p =1
⎠⎝ p =1
⎠⎦
p =1
(11) S ( i ,q ) 2 = ⎣
n(n − 1)
(12) S ( i ,q ) = S ( i ,q )
2
S = nilai peragam sampel
i
= angka suatu titik posisi dari fungsi ( 1..16 )
q = angka suatu titik posisi dari fungsi ( 1..16 )
Jika i = q maka hasil S(i,q) merupakan nilai ragam (variance), dan jika nilai
i ≠ q maka S(i,q) merupakan nilai peragam (covariance). Sehingga diperoleh matriks
peragam sampel gabungan, sebagai berikut:
20
Tabel 4.5 Matriks peragam sampel gabungan
⎡ S (1,1 )
⎢ S (2 ,1 )
⎢
SG = ⎢
M
⎢
M
⎢
⎢⎣ S (16 ,1 )
S (1, 2 )
S (1, 3 )
L
O
O
O
S (16 , 2 )
S (16 , 3 ) L
S (1,16 ) ⎤
S (2 ,16 ) ⎥⎥
⎥
M
⎥
M
⎥
S (16 ,16 )⎥⎦
4.2.2 Uji Statistik T2-Hotteling
Sebelum membangun fungsi diskriminan, kita perlu melakukan pengujian
perbedaan vektor nilai rata-rata dari kedua populasi untuk mengetahui apakah
ada nilai rata-rata dari sifat yang dipelajari itu yang berbeda secara statistik.
Untuk menguji perbedaan vektor nilai rata-rata diantara dua populasi dapat
menggunakan statistik T2-Hotteling.
Pengujian perbedaan vektor nilai rata-rata diantara dua populasi
dilakukan dengan jalan merumuskan hipotesis berikut :
Tabel 4.6 Hipotesis uji statistik T2-Hotteling
Ho : T1 = T2
:
artinya vektor nilai rata-rata dari populasi lakilaki sama dengan dari populasi perempuan
H1 : T1 ≠ T2
:
artinya kedua vektor nilai rata-rata itu berbeda
Pengujian terhadap hipotesis (Tabel 4.6 ) dilakukan dengan menggunakan
uji statistik T2-Hotteling yang dirumuskan, sebagai berikut :
(
)
(
′
n1n 2
V 1 − V 2 × S −1 × V 1 − V 2
n1 + n 2
(13)
T 12 =
(14)
Fα ; p1; p 2
)
berdasarkan interpolasi linear dari Tabel Distribusi F dengan :
α
= taraf normal ( dipilih α = 0.05 )
p1
= i = 16 (banyaknya variabel pembeda sifat V)
21
p2
= n1 + n2 – i – 1
= 20 + 20 – 16 – 1
= 23
(15)
T 22 =
(n1 + n 2 − 2)i × Fα ; p1; p 2
n1 + n 2 − i − 1
Apabila nilai T12 > T22, maka tolak H0. Sehingga dapat disimpulkan bahwa
kedua vektor nilai rata-rata yang diuji berbeda nyata pada taraf nyata α. dan ini
berarti penelitian bisa dilanjutkan dengan perhitungan fungsi diskriminan.
4.2.3 Fungsi Diskriminan Linear
Fungsi diskriminan yang mencirikan perbedaan sifat-sifat yang dipelajari
dapat dibangun apabila telah diketahui adanya perbedaan diantara kedua
kelompok populasi, melalui statistik T2-Hotteling. Fungsi diskriminan linear
dibangun berdasarkan koefisien-koefisien fungsi diskriminan yang dapat
diperoleh melalui persamaan berikut :
(16)
⎡ e1 ⎤
⎢ e2 ⎥
′
⎢ ⎥ = V 1 − V 2 × S −1
⎢M⎥
⎢ ⎥
⎣e16 ⎦
(
)
Dengan demikian dapat dibentuk model fungsi diskriminan linear dan
dihasilkan nilai fungsi diskriminan linear sebagai penentu jenis kelamin
manusia yang menjadi tujuan utama penelitian ini. Persamaan fungsi
diskriminan linear adalah sebagai berikut :
(17)
∧
16
Yk = ∑ ei × d ( i ,k )
i =1
22
(17’)
∧
Yk = e1 × d (1,k ) + e 2 × d ( 2,k ) + K + e16 × d (16,k )
i
= angka suatu titik posisi dari fungsi ( 1..16 )
k
= jumlah sampel yang diuji ( 1 .. 40 )
∧
Yk
= nilai fungsi diskriminan linear pada sampel ke- k
ei
= koefisien fungsi diskriminan linear ke- i
d ( i ,k ) = normalized harmonic amplitudes masing-masing
sebanyak i pada setiap sampel yang berjumlah k
4.3 Perancangan Program Pemecahan Masalah
4.3.1 Borland Delphi
Menurut StrawberryFrog (2001), Borland Delphi versi 1.0 pertama kali
diperkenalkan pada hari Valentine tahun 1995. Pada waktu itu, development
environtment yang banyak digunakan Microsoft Windows adalah Microsoft
Visual Basic dan Microsoft C++. Pembuatan Borland Delphi bertujuan untuk
memberikan kemudahan kepada para programmer dalam membuat program
secara
visual,
dengan
cara
menggabungkan
kemudahan
penggunaan
environtment dari Visual Basic dan ketangguhan dari object oriented milik
Microsoft C++.
Arsitek utama dari 3 versi pertama Borland Delphi adalah Anders
Hejsberg. Setelah itu dia bergabung dengan Microsoft dan menciptakan suatu
set class untuk java yang disebut WFC (Windows Foundation Classes). Project
selanjutnya adalah bahasa C#, yang mirip dengan Java tapi menggunakan
beberapa ide yang bergaya Delphi.
23
4.3.2 Perancangan Layar
Penulis merancang program yang terdiri atas 1 menu utama (Home) yang
dapat terhubung dengan 3 menu khusus ( Password, Training dan Recognize ).
Program ini dibuat dengan piranti lunak Borland Delphi versi 7.0
.
A. Rancangan Layar Menu Home
Gambar 4.3 – Rancangan Layar Menu Home
Keterangan yang terdapat pada tampilan layar tersebut adalah sebagai
berikut .
•
Judul form dengan tulisan ’Program Komputer Aplikasi Penentuan
Jenis Kelamin Manusia Dewasa Berdasarkan Bentuk Dahi Pada Citra
Cephalometry’.
24
•
Tombol ’Training’ memiliki fungsi untuk membuka layar menu
khusus Training. Namun sebelum itu, layar menu Password akan
terbuka.
•
Tombol ’Recognize’ memiliki fungsi untuk membuka layar menu
khusus Recognize.
•
Terdapat keterangan mengenai identitas penulis, tujuan penulisan, dan
dosen pembimbing dari penulis.
•
Tombol dengan tanda ’X’ disebelah kanan bawah layar memiliki
fungsi untuk keluar dari program.
B. Rancangan Layar Menu Password
Gambar 4.4 – Rancangan Layar Menu Password
Keterangan yang terdapat pada tampilan layar tersebut adalah sebagai
berikut .
•
Terdapat label ’User Name’ dan kotak disampingnya untuk masukan
nama dari user yang menjalankan program aplikasi.
•
Tersedia label ’Password’ dan kotak disampingnya untuk masukan
password dari user yang ingin dan diijinkan menjalankan Training.
•
Tombol ’Cancel’ berfungsi untuk membatalkan proses menjalankan
Training, sehingga akan muncul kembali menu Home.
•
Tombol ’OK’ berfungsi untuk menilai benar atau tidak ’User Name’
dan ’Password’ yang baru dimasukkan, kemudian jika benar menu
Training akan ditampilkan.
25
C. Rancangan Layar Menu Training
Gambar 4.5 – Rancangan Layar Menu Training
Keterangan yang terdapat pada tampilan layar tersebut adalah
sebagai berikut.
•
Pada bagian kiri bawah terdapat label ‘image ke’ dan sebuah kotak
yang berfungsi untuk menghitung banyaknya image cephalometry
yang telah dibuka dan diteliti.
•
Pada bagian ‘Proses’ tersedia 8 langkah, yang dapat dijalankan
dengan menekan tombol yang dimiliki oleh masing-masing langkah.
1.
Membuka image dan menampilkannya pada kotak ‘Image
Cephalometry’
2.
Menyimpan koordinat titik Nasion dan Titik Bregma.
3.
Tombol ini akan melakukan 3 hal, yaitu :
¾
Menghubungkan
Titik
Nasion
dan
Bregma
dan
menjadikan garis tersebut sebagai basis x
¾
Menampilkan bagian dahi pada kotak ’32 Titik Sampel’
¾
Membagi daerah tersebut menjadi 32 bagian dari (X0, Y0)
sampai (X31, Y31), kemudian menyimpan nilai tersebut
4.
Mengolah nilai Y0 sampai Y31, untuk mendapatkan nilai ai, bi,
c i,
dan
di .
kemudian
menampilkan
kotak ’Normalized Harmonic Amplitudes’
nilai
di
pada
26
5.
Menyimpan nilai di
6.
Mengharuskan trainer untuk melibatkan data cephalometry
sebanyak 40 buah (secara berurutan 20 laki-laki dan 20
perempuan), dengan mengulang langkah 1 – 6.
7.
Mengolah nilai-nilai di untuk mendapatkan nilai ei dan Yk,
kemudian menampilkannya pada kotak ‘Koefisien Fungsi
Diskriminan’ dan ‘Nilai Fungsi Diskriminan’.
8.
Hitung range Y1 – Y20 dan Y21 – Y40 dan menampilkannya
pada kotak ‘Kesimpulan’.
•
Pada kanan bawah terdapat tombol ‘Back to Home’ untuk kembali
ke layar menu ‘Home‘ dan tombol dengan tanda ’X’ memiliki
fungsi untuk keluar dari program.
D. Rancangan Layar Menu Recognize
Gambar 4.6 – Rancangan Layar Menu Recognize
Keterangan yang terdapat pada tampilan layar tersebut adalah
sebagai berikut.
•
Pada bagian ‘Proses’ tersedia 6 langkah, yang dapat dijalankan
dengan menekan tombol yang dimiliki oleh masing-masing langkah,
yaitu :
27
1.
Membuka image dan menampilkannya pada kotak ‘Image
Cephalometry’
2.
Menyimpan koordinat titik Nasion dan Titik Bregma
3.
Tombol ini akan melakukan 3 hal, yaitu :
¾
Menghubungkan
Titik
Nasion
dan
Bregma
dan
menjadikan garis tersebut sebagai basis x
¾
Menampilkan bagian dahi pada kotak ’32 Titik Sampel’
¾
Membagi daerah tersebut menjadi 32 bagian dari (X0, Y0)
sampai (X31, Y31), kemudian menyimpan nilai tersebut
4.
Tombol ini akan melakukan 2 hal, yaitu :
¾
Mengolah nilai Y0 sampai Y31, untuk mendapatkan nilai
ai, bi, ci, dan di. kemudian menampilkan nilai di pada
kotak ’Normalized Harmonic Amplitudes’.
¾
Menampilkan nilai ei pada kotak ‘Koefisien Fungsi
Diskriminan’
5.
Menghitung nilai Yk dan menampilkannya pada kotak ‘Nilai
Fungsi Diskriminan’.
6.
Membandingkan nilai Yk dengan range penentu jenis kelamin,
yang merupakan hasil training. Kemudian menampilkan
hasilnya pada kotak ‘Kesimpulan’.
•
Pada kanan bawah terdapat tombol ‘Back to Home’ untuk kembali
ke layar menu ‘Home‘ dan tombol dengan tanda ’X’ memiliki
fungsi untuk keluar dari program.
4.3.3 Diagram Alir
Diagram Alir merupakan alat bantu pemrograman. Bagan alir (flowchart)
membantu programmer dalam mengorganisasikan pemikiran mereka dalam
pemrograman, terutama bila dibutuhkan penalaran yang tajam dalam logika
prosedur suatu program (Jones, 1980).
28
Simbol-simbol yang sering digunakan untuk diagram alir adalah sebagai
berikut :
1.
Proses
•
Berupa proses/ pengolahan, misalnya perhitungan
•
Untuk predefined process
2.
Operasi Input / Output
3.
Operasi Manual Input
4.
Panah, menghubungkan antar komponen dan
menunjukkan arah
5.
Decision, berupa pertanyaan atau penentuan suatu
keputusan
6.
Terminal, untuk menandai awal atau akhir program
7.
Preparation, untuk inisialisasi suatu nilai
8.
Connector,
sebagai
penghubung
dalam
satu
halaman
9.
Off Page Connector, sebagai penghubung antar
halaman
29
Gambar 4.7 – Perancangan Flowchart Proses Training
30
Gambar 4.8 – Perancangan Flowchart Proses Perhitungan Input Cephalometry
31
Gambar 4.9 – Perancangan Flowchart Proses Analisis Fourier
32
Gambar 4.10 – Perancangan Flowchart Proses Analisis Diskriminan
33
Gambar 4.11 – Perancangan Flowchart Proses Perhitungan Nilai S
34
Gambar 4.12 – Perancangan Flowchart Proses Perhitungan Nilai V
35
Gambar 4.13 – Perancangan Flowchart Proses Perhitungan Output Training
36
Gambar 4.14 – Perancangan Flowchart Proses Recognize
37
Gambar 4.15 – Perancangan Flowchart Proses Perhitungan Output Recognize