PROPOSAL TUGAS AKHIR

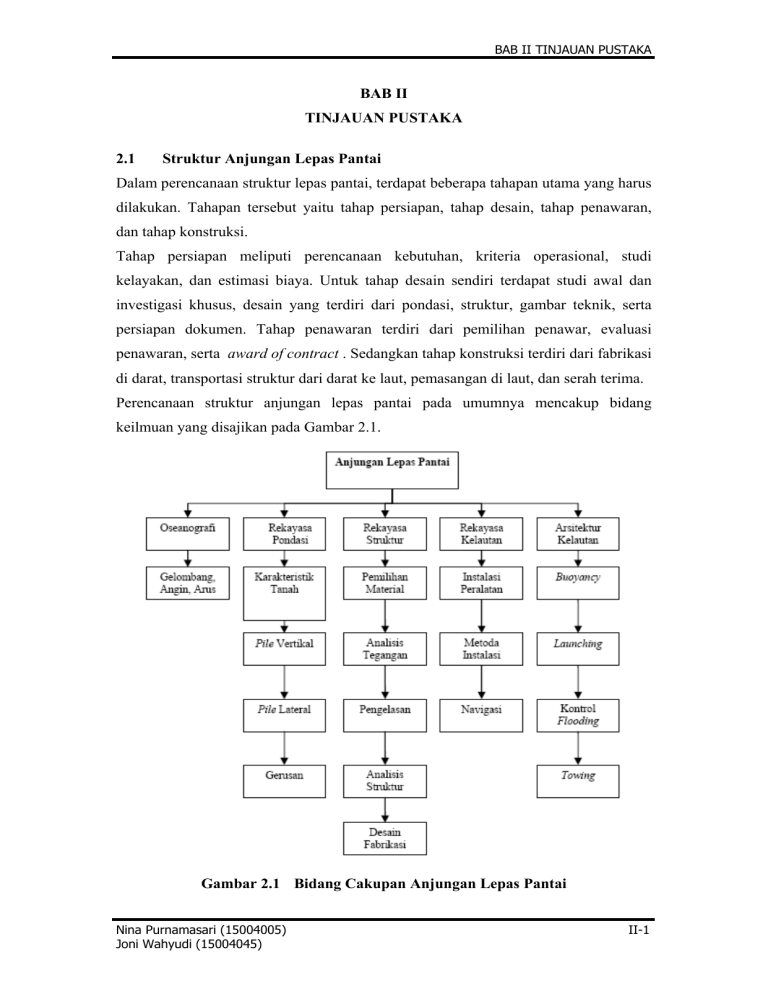
BAB II TINJAUAN PUSTAKA
BAB II
TINJAUAN PUSTAKA
2.1
Struktur Anjungan Lepas Pantai
Dalam perencanaan struktur lepas pantai, terdapat beberapa tahapan utama yang harus
dilakukan. Tahapan tersebut yaitu tahap persiapan, tahap desain, tahap penawaran,
dan tahap konstruksi.
Tahap persiapan meliputi perencanaan kebutuhan, kriteria operasional, studi
kelayakan, dan estimasi biaya. Untuk tahap desain sendiri terdapat studi awal dan
investigasi khusus, desain yang terdiri dari pondasi, struktur, gambar teknik, serta
persiapan dokumen. Tahap penawaran terdiri dari pemilihan penawar, evaluasi
penawaran, serta award of contract . Sedangkan tahap konstruksi terdiri dari fabrikasi
di darat, transportasi struktur dari darat ke laut, pemasangan di laut, dan serah terima.
Perencanaan struktur anjungan lepas pantai pada umumnya mencakup bidang
keilmuan yang disajikan pada Gambar 2.1.
Gambar 2.1 Bidang Cakupan Anjungan Lepas Pantai
Nina Purnamasari (15004005)
Joni Wahyudi (15004045)
II-1
BAB II TINJAUAN PUSTAKA
Untuk perencanaan dan desain struktur anjungan lepas pantai, diperlukan standar
spesifikasi yang sesuai. Peraturan perencanaan dan spesifikasi standar yang digunakan
adalah:
1.
API RP 2A-WSD, 21st Edition “Recommended Practice for Planning,
Designing, and Cosntruction Fixed Offshore Platform”. American
Petroleum Institute, Washington DC, July 1st, 2000.
2.
AISC 9th Edition “Manual of Steel Construction, Allowable Stress
Design”. American Institute of Steel Construction, AISC, New York
1989.
Beberapa jenis anjungan lepas pantai yang umum digunakan, dapat dikelompokkan
sebagai berikut:
1. Anjungan lepas pantai tipe tetap (fixed offshore platform)
Anjungan lepas pantai tipe tetap merupakan anjungan yang paling sering digunakan
dalam kegiatan eksploitasi minyak dan gas. Anjungan ini dikatakan tetap, karena
tidak mengalami perpindahan atau deformasi yang berarti dalam beroperasi menahan
beban-beban yang bekerja.
Contoh anjungan tipe tetap antara lain :
a. Jacket Platform
Anjungan tipe jacket ini dikembangkan untuk beroperasi di laut dangkal dan laut
sedang (maksimal pada kedalaman 320 m) yang dasarnya tebal, lunak, dan berlumpur.
Setelah jacket ditempatkan di posisi yang diinginkan, pile dimasukkan melalui kaki
jacket dan kemudian dipancang dengan hammer sampai menembus lapisan tanah
keras.
Nina Purnamasari (15004005)
Joni Wahyudi (15004045)
II-2
BAB II TINJAUAN PUSTAKA
Gambar 2.2 Anjungan Tipe Jacket
b. Caissons Platform
Merupakan platform kecil dengan deck kecil, digunakan untuk operasi di laut dangkal
(tidak lebih dari 60m), dengan kandungan minyak yang tidak terlalu banyak. Pile
yang dipancang hingga kedalaman yang cukup untuk menyokong deck kecil.
Nina Purnamasari (15004005)
Joni Wahyudi (15004045)
II-3
BAB II TINJAUAN PUSTAKA
Gambar 2.3 Anjungan Tipe Caissons
c. Concrete Gravity Platform
Platform jenis ini menggunakan pondasi yang terbuat dari beton, dimana pondasi
yang berat ini menyokong beberapa tower yang kemudian menyokong deck baja.
Biasanya digunakan apabila tanah keras di dasar laut tidak jauh dari permukaan
lumpur.
Gambar 2.4 Concrete Gravity Platform
2. Anjungan tipe terapung (floating offshore platform)
Anjungan tipe terapung ini akan bergerak akibat gaya luar seperti gelombang dan arus
laut yang bekerja padanya, dikarenakan kekakuannya tidak besar. Namun pergerakan
Nina Purnamasari (15004005)
Joni Wahyudi (15004045)
II-4
BAB II TINJAUAN PUSTAKA
yang terjadi masih dalam batas-batas yang diijinkan, sehingga tidak mengganggu
kegiatan operasionalnya.
Contoh anjungan tipe terapung antara lain:
a. Tension Leg Platform
Anjungan ini biasanya digunakan pada laut dalam (hingga kedalaman 2000 m),
menggunakan kaki-kaki panjang dan fleksibel sehingga memungkinkan pergerakan
arah lateral dengan sedikit pergerakan arah vertikal.
Gambar 2.5 Tension Leg Platform
b. Jack up Rigs
Anjungan tipe ini berupa anjungan terapung yang ditarik dengan kapal tunda menuju
lokasi pengeboran yang beroperasi di perairan dangkal dan tenang. Setelah berada di
lokasi pengeboran, kaki-kakinya diturunkan hingga menyentuh dasar laut.
Gambar 2.6 Jack Up Rigs
Nina Purnamasari (15004005)
Joni Wahyudi (15004045)
II-5
BAB II TINJAUAN PUSTAKA
c. Semi Submersible Rigs
Anjungan tipe ini beroperasi dalam keadaan terapung, dimana terdapat bagian
lambung yang diisi dengan air untuk memberikan kestabilan pada rig. Rig-rig pada
anjungan ditambat (mooring) ke dasar laut oleh sauh.
Gambar 2.7 Semi Submersible Rigs
Pemilihan anjungan lepas pantai yang akan digunakan secara umum terkait dengan
kedalaman laut, faktor ekonomi, dan fungsi dari anjungan itu sendiri. Gambar berikut
ini menunjukkan jenis-jenis platform berdasarkan kedalamannya.
Nina Purnamasari (15004005)
Joni Wahyudi (15004045)
II-6
BAB II TINJAUAN PUSTAKA
Gambar 2.8 Jenis Platform Berdasarkan Kedalaman
Anjungan tersebut harus kuat menahan beban-beban yang bekerja. Bebanbeban yang
bekerja pada anjungan lepas pantai diantaranya beban mati, beban hidup, dan beban
lingkungan (arus, gelombang, angin, gempa, salju, es, dan suhu). Akibat banyaknya
beban-beban yang bekerja, sehingga diperlukan analisis yang tepat dan akurat pada
desain sebuah anjungan lepas pantai sesuai dengan standar yang ada.
2.2.
Kriteria Pembebanan
Anjungan lepas pantai harus di disain berdasarkan beban-beban yang diklasifikasikan
dalam beberapa kategori sebagai berikut:
1.
Beban tetap (Beban Mati)
2.
Beban saat kondisi operasi
3.
Beban lingkungan termasuk beban gempa
4.
Beban konstruksi-instalasi
5.
Beban impak
Beban lingkungan adalah beban yang bekerja pada struktur platform akibat dari
fenomena alam, antara lain akibat angin, arus, dan gelombang. Beban lingkungan ini
harus diperhitungkan dari segala arah kecuali jika kondisi tertentu, dapat dilakukan
asumsi yang berbeda.
Nina Purnamasari (15004005)
Joni Wahyudi (15004045)
II-7
BAB II TINJAUAN PUSTAKA
Gambar 2.9 Beban Lingkungan Pada Struktur Offshore
Data yang tersedia untuk beban ini diolah untuk menggambarkan struktur platform
dalam kondisi lingkungan operasional maupun ekstrim.
1.
Kondisi lingkungan operasional
Kondisi normal diharapkan terjadi berulangkali selama struktur beroperasi. Kondisi
ini penting dalam tahap konstruksi dan tahap masa
layan struktur platform.
2.
Kondisi lingkungan ekstrim
Kondisi lingkungan ekstrim yang jarang terjadi selama struktur beroperasi. Kondisi
ini penting untuk memformulasikan beban rencana platform.
2.2.1
Beban Mati
Beban mati pada struktur platform adalah berat dari struktur platform itu sendiri
dan semua peralatan permanen serta perlengkapan struktur yang tidak berubah selama
pengoperasian.Yang termasuk dalam beban mati struktur platform adalah:
1.
Berat struktur platform di udara, termasuk berat dari pile, grout, dan
ballast jika ada.
2.
Berat peralatan dan perlengkapan struktur yang sifatnya permanen
pada platform.
3.
Gaya hidrostatik yang bekerja pada struktur dibawah permukaan laut,
termasuk tekanan dan gaya angkat.
Nina Purnamasari (15004005)
Joni Wahyudi (15004045)
II-8
BAB II TINJAUAN PUSTAKA
2.2.2
Beban Hidup
Beban hidup pada struktur platform adalah beban-beban yang bekerja pada platform
selama masa layannya dan mungkin dapat berubah saat pengoperasian.
Yang termasuk dalam beban hidup struktur platform adalah:
1.
Beban perlengkapan pengeboran dan perlengkapan produksi yang bisa
dipasang dan dipindahkan dari platform.
2.
Berat dari ruang tempat tinggal (living quarters), heliport, dan
perlengkapan penunjang lainnya yang bisa dipasang dan dipindahkan
dari platform.
3.
Berat dari suplai kebutuhan dan benda cair lainnya yang mengisi
tangki penyimpanan.
4.
Gaya yang bekerja pada struktur selama operasional seperti
pengeboran, penambatan kapal, dan beban helikopter.
5.
Gaya yang mengenai struktur dari penggunaan crane diatas deck.
2.2.3
Angin
2.2.3.1
Gaya Angin
Gaya angin yang bekerja disebabkan oleh gesekan udara dengan permukaan dari
struktur dan perbedaan tekanan antara bagian depan dan belakang dari struktur. Beban
angin dikenakan pada bagian struktur yang berada diatas permukaan air.
Beban angin diperhitungkan dengan menggunakan persamaan (2.1) dibawah ini:
F=
keterangan:
ρ
1
ρ Cs A V2
2
(2.1)
= massa jenis udara
Cs = koefisien bentuk
A = luas objek (ft2)
V = kecepatan angin (mph)
ρ biasanya dianggap konstan terhadap perubahan tekanan dan suhu. Untuk suhu 60° F
dan tekanan 14,7 lb/in persamaannya menjadi:
F = 0,00256 Cs A V2
keterangan:
(2.2)
Cs = koefisien bentuk
A = luas objek (ft2)
V = kecepatan angin (mph)
Nina Purnamasari (15004005)
Joni Wahyudi (15004045)
II-9
BAB II TINJAUAN PUSTAKA
Harga koefisien bentuk yang biasa digunakan dalam perancangan dan analisis struktur
lepas pantai diperlihatkan dalam Tabel 2.1.
Tabel 2.1 Koefisien Bentuk
Bagian anjungan
Balok
Bagian silinder
Sisi anjungan
Area proyeksi anjungan keseluruhan
Koefisien Bentuk
1.5
0.5
1.5
1
Kecepatan angin berubah sesuai ketinggian. Koreksi kecepatan angin apabila tidak
sama dengan ketinggian referensi disajikan dengan persamaan:
⎛ z
Vz = V × ⎜⎜
⎝ zR
keterangan:
⎞
⎟⎟
⎠
m
(2.3)
V = kecepatan angin pada 32,8 ft diatas permukaan laut
z
= elevasi disain
zR = 32,8 ft diatas permukaan laut
m = 1/8 untuk angin tetap
= 1/13 untuk angin badai
2.2.3.2
Gaya Angin Pada Bidang Miring
Untuk permukaan yang tidak tegak lurus terhadap arah angin, gaya angin harus
diperhitungkan dengan menggunakan persamaan berikut ini.
F=
keterangan:
1
ρ C A V2 cos2 α
2
(2.4)
α = sudut arah angin dan arah normal dari permukaan elemen
A = luas area pada arah normal elemen
Kecepatan angin pada arah normal elemen menjadi V cos α. Untuk silinder dengan
panjang L dan diameter D atau untuk pelat datar dengan panjang L dan lebar D, maka
A = L x D. Setelah F didapat, besar beban diproyeksikan kepada arah x dan y,
sehingga Fx = F cos α dan Fy = F sin α
Gambar 2.10 Proyeksi Bidang Angin
Nina Purnamasari (15004005)
Joni Wahyudi (15004045)
II-10
BAB II TINJAUAN PUSTAKA
2.2.4
Gelombang
Gelombang laut terjadi karena adanya gaya-gaya yang bekerja pada fluida. Tiupan
angin dan jatuhnya benda pada permukaan air dapat menimbulkan gelombang.
Parameter–parameter terpenting dalam menggambarkan gelombang (Gambar 2.4)
adalah:
1.
Panjang gelombang L (jarak horisontal antara dua puncak gelombang
atau dua lembah gelombang yang saling berurutan).
2.
Tinggi gelombang H (jarak vertikal antara puncak gelombang dan
lembah gelombang).
3.
Perida gelombang T (waktu yang ditempuh untuk mencapai satu
lintasan gelombang).
4.
Kedalaman perairan h, dimana gelombang tersebut merambat.
Gambar 2.11 Sketsa Profil Gelombang
keterangan:
L
= panjang gelombang
H
= tinggi gelombang
A
= amplitudo gelombang (1/2 H)
C
= cepat rambat gelombang
u
= kecepatan horisontal partikel air
w
= kecepatan vertikal partikel air
MWL = Mean Water Level
η(x,t) = elevasi muka air di lokasi x pada saat t
h
= kedalaman perairan
Nina Purnamasari (15004005)
Joni Wahyudi (15004045)
II-11
BAB II TINJAUAN PUSTAKA
2.2.4.1
Teori Gelombang Airy / Linier
Teori ini berdasarkan asumsi bahwa tinggi gelombang jauh lebih kecil jika
dibandingkan dengan panjang gelombang L dan kedalaman h, jadi H<<L,h. Dengan
asumsi bahwa H<<L,h tersebut, maka nilai suku-suku tak linier pada syarat batas
kecil dan dapat diabaikan serta syarat batas di permukaan dapat diterapkan di z = 0,
bukan di z = η lagi.
Dari syarat batas dinamis, dengan membuat rata-rata η = 0 maka C(t) = 0 sehingga
η =
H
cos (kx – ωt)
2
(2.5)
Dari asumsi tersebut, maka menghasilkan persamaan berikut :
¾ Kecepatan partikel air pada arah horisontal u,
u= −
∂φ H cosh k (h + z )
= ω
cos(kx − ωt )
∂x
2
sinh kh
(2.6)
atau
u=
gHk cosh k (h + z )
cos(kx − ωt )
2ω
sinh kh
(2.7)
¾ Percepatan partikel air arah horisontal adalah,
∂u H 2 cosh k (h + z )
sin (kx − ωt )
= ω
2
sinh kh
∂t
(2.8)
¾ Kecepatan partikel air arah vertikal w,
w= −
∂φ H sinh k (h + z )
sin (kx − ωt )
= ω
2
sinh kh
∂x
(2.9)
¾ Percepatan partikel air arah vertikal adalah,
∂w H 2 sinh k (h + z )
cos(kx − ωt )
= ω
2
sinh kh
∂t
(2.10)
Kecepatan dan percepatan merupakan fungsi dari posisi, sehingga terdapat beda fase
sebesar 90°, kecepatan horisontal akan mempunyai nilai yang ekstrim pada saat fase
(kx – ωt) = 0, π,.... atau dibawah puncak dan lembah gelombang.
2.2.4.2
Teori Gelombang Stokes
Karena masalah konvergensi yang lebih sulit untuk kondisi laut dangkal, teori
gelombang Stokes orde ke-5 dianggap valid untuk kondisi perairan dimana rasio
kedalaman h/L lebih besar dari
Nina Purnamasari (15004005)
Joni Wahyudi (15004045)
1
. Kondisi ini umumnya sesuai dengan gelombang
10
II-12
BAB II TINJAUAN PUSTAKA
badai (storm wave) yang biasanya diperhitungkan dalam perancangan bangunan lepas
pantai.
Untuk tinggi gelombang H, bilangan gelombang k, dan frekuensi ω, yang bergerak
dalam arah sumbu x, permukaan gelombang Stokes dituliskan;
η =
1 5
∑ Fn cos n (kx – ωt)
k n =1
(2.11)
dimana
F1 = a
F2 = a2 F22 + a4 F24
F3 = a3 F33 + a5 F35
(2.12)
4
F4 = a F44
F5 = a5 F55
F22, F24, dan seterusnya, merupakan parameter profil (bentuk) gelombang yang
tergantung pada kh dan a merupakan parameter tinggi gelombang didalam persamaan
berikut:
[
]
kH = 2 a + a 3 F33 + a 5 (F35 + F55 )
(2.13)
Kecepatan horisontal (u) dan kecepatan vertikal (w) partikel air gelombang Stokes
(pada posisi x, waktu t, dan sejauh z dari dasar perairan) adalah:
u
=
ω
5
∑G
k
n =1
w =
ω
n
5
∑G
k
n =1
n
cosh nkz
cos n (kx – ωt)
sinh nkh
(2.14)
sinh nkz
sin n (kx – ωt)
sinh nkh
(2.15)
dimana G1, G2, dst dituliskan sebagai berikut;
G1 = a G11 + a3 G13 + a5 G15
(
3 (a G
G2 = 2 a 2 G22 + a 4 G24
G3 =
3
33
+ a 5 G35
)
)
(2.16)
G4 = 4 a4 G44
G5 = 5 a5 G55
G11, G13, dst adalah parameter kecepatan gelombang yang bergantung pada kh.
Persamaan parameter F22, F24, G11, dst diberikan oleh Skjelbreia dan Hendrickson (F22
= B22, F24 = B24,dst dan G11 = A11 sinh kh, G24 = A24 sinh 2kh, dst). Tabel 2.2 dan
Nina Purnamasari (15004005)
Joni Wahyudi (15004045)
II-13
BAB II TINJAUAN PUSTAKA
tabel 2.3 memberikan pendekatan parameter-parameter tersebut untuk berbagai harga
h kh
.
=
L 2π
Tabel 2.2 Harga Parameter Bentuk Gelombang
Hubungan antara frekuensi gelombang dengan bilangan gelombang dalam teori
Stokes;
(
)
ω2 = gk 1 + a 2 C1 + a 4 C2 tanh kh
(2.17)
dimana C1 dan C2 adalah parameter frekuensi gelombang, tabel 2.3 memberikan
ilustrasi harga parameter frekuensi gelombang untuk berbagai harga h/L.
Kecepatan gelombang c ditentukan seperti pada teori gelombang Airy, c = σ
k
,
dimana kecepatan gelombang Stokes orde ke-5 dituliskan sebagai berikut;
c
=
(
)
⎡g
⎤
2
4
⎢ k 1 + a C1 + a C 2 tanh kh⎥
⎦
⎣
1
2
(2.18)
Tabel 2.3 Harga Parameter Kecepatan Gelombang
Nina Purnamasari (15004005)
Joni Wahyudi (15004045)
II-14
BAB II TINJAUAN PUSTAKA
Tabel 2.4 Parameter Frekuensi dan Tekanan Gelombang
Setelah semua koefisien dalam persamaan untuk kecepatan partikel akibat gelombang
Stokes ditentukan, percepatan horisontal ax dan percepatan vertikal az dapat
ditentukan dengan persamaan;
ax =
∂u
∂u
∂u
+u
+w
∂t
∂x
∂z
(2.19)
az =
∂w
∂w
∂w
+u
+w
∂z
∂w
∂x
(2.20)
dengan menuliskan koefisien kecepatan sebagai:
Un = Gn
cosh nkz
sinh nkh
(2.21)
Wn = Gn
sinh nkz
sinh nkh
(2.22)
dengan operasi trigonometri, persamaan percepatan partikel air dapat dituliskan dalam
bentuk eksplisit berikut;
ax =
az =
kc 2
2
5
∑R
n
n =1
kc 2
−
2
sin n(kx − ωt )
5
∑S
n =1
n
cos n(kx − ωt )
(2.23)
(2.24)
dimana koefisien Rn dan Sn dituliskan sebagai fungsi Un dan Wn berikut ini;
R1 = 2U1 – U1U2 – W1W2 – U2U3 – W2W3
R2 = 4U2 – U12 + W12 – 2U1U3 – 2W1W3
R3 = 6U3 – 3U1U2 + 3W1W2 – 3U1U4 – 3W1W4
(2.25)
R4 = 8U4 – 2U22 + 2W22 – 4U1U3 + 4W1W3
R5 = 10U5 – 5U1U4 – 5U2U3 + 5W1W4 + 5W2W3
dan
Nina Purnamasari (15004005)
Joni Wahyudi (15004045)
II-15
BAB II TINJAUAN PUSTAKA
S0 = -2U1W1
S1 = 2W1 – 3U1W2 – 3U2W1 – 5U2W3 – 5U3W2
S2 = 4W2 – 4U1W3 – 4U3W1
S3 = 6W3 – U1W2 + U2W1 – 5U1W4 – 5U4W1
(2.26)
S4 = 8W4 – 2U1W3 + 2U3W1 + 4U2W2
S5 = 10W5 – 3U1W4 + 3U4W1 – U2W3 + U3W2
Tekanan akibat gelombang dan kontribusi hidrostatik dapat ditentukan dan komponen
kecepatan dengan mensubstitusikan pada persamaan berikut,
p
=
ρ
ω
k
u−
1
ρg 2
ρ u 2 + w2 −
a C 3 + a 4 C 4 + kz '
2
k
(
)
(
)
(2.27)
dimana z’ = z – h, C3 dan C4 adalah parameter tekanan yang tergantung pada kh atau
h/L, harga C3 dan C4 dapat dilihat pada tabel 2.4
2.2.4.3
Analisis Statik Gelombang
Beban gelombang memiliki sifat dinamis. Untuk sebagian besar kedalaman perairan
rencana, beban ini dapat terwakili oleh beban statik yang ekuivalen.
Urutan langkah perhitungan dari gaya gelombang statik deterministik pada anjungan
lepas pantai tipe tetap, dimulai dengan penentuan tinggi gelombang desain dan perida
gelombang yang berkaitan, kedalaman laut pada saat badai, dan profil arus. Prosedur
perhitungan gaya gelombang menurut API RP2A-WSD Section 2.3.1, mengikuti
langkah berikut ini:
1.
Menentukan perioda gelombang nyata (Apparent Wave Period),
ditentukan dengan memperhitungkan efek Doppler akibat arus pada
gelombang.
2.
Kinematika gelombang dua dimensi ditentukan dari teori gelombang
yang sesuai untuk suatu tinggi gelombang, kedalaman laut saat badai,
dan apparent wave period.
3.
Komponen mendatar dari kecepatan dan percepatan partikel yang
diakibatkan oleh gelombang dikurangi oleh faktor kinematika
gelombang, yang terutama mempertimbangkan arah penyebaran
gelombang.
4.
Arus efektif lokal ditentukan dengan mengalikan arus yang diketahui
dengan faktor hambatan arus (current blockage factor).
Nina Purnamasari (15004005)
Joni Wahyudi (15004045)
II-16
BAB II TINJAUAN PUSTAKA
5.
Arus efektif lokal dikombinasikan searah dengan kinematika
gelombang untuk menentukan kecepatan dan percepatan fluida lokal
yang akan digunakan pada persamaan Morison.
6.
Ukuran elemen diperbesar akibat marine growth.
7.
Koefisien hidrodinamik (drag dan inertia) ditentukan sebagai fungsi
dari parameter gelombang dan arus, bentuk elemen, kekasaran (akibat
marine growth), ukuran, dan arah.
8.
Koefisien gaya gelombang untuk kumpulan konduktor berkurang
karena adanya conductor shielding factor.
9.
Pengembangan model hidrodinamik untuk
riser
dan struktur
tambahan.
10.
Gaya gelombang / arus lokal dihitung untuk seluruh elemen anjungan,
konduktor,
riser , dan struktur tambahan, menggunakan persamaan
Morison.
11.
Gaya keseluruhan dihitung sebagai penjumlahan vektor dari seluruh
gaya lokal.
Gambar 2.12 Prosedur Perhitungan Gaya Akibat Gelombang dan Arus Untuk
Analisis Statik
Nina Purnamasari (15004005)
Joni Wahyudi (15004045)
II-17
BAB II TINJAUAN PUSTAKA
2.2.4.4
Apparent Wave Period
Arus yang searah dengan gelombang cenderung memperbesar panjang gelombang,
sedangkan arus yang berlawanan memperkecil panjang gelombang. Apparent wave
period, Tapp, adalah perioda gelombang relatif terhadap arus sejajar efektif. Untuk
gelombang yang merambat pada suatu profil arus, penentuan apparent wave period
dilakukan dengan menyelesaikan persamaan di bawah ini:
λ
T
=
λ
Tapp
Tapp2
+ V1
=
g
2πλ
tanh (2πd / λ )
4π / λ
⎡ 4π ( z + d ) ⎤
U c ( z ) cosh ⎢
V1 =
∫
⎥dz
sinh (4πd / λ ) d
λ
⎣
⎦
(2.28)
0
dimana:
λ
= panjang gelombang
d
= kedalaman laut saat badai
(2.29)
Uc(z) = komponen profil arus untuk kondisi tetap pada arah
gelombang z
2.2.4.5
g
= percepatan gravitasi
V1
= kecepatan arus sejajar efektif
T
= perioda gelombang relatif terhadap objek tetap
Kinematika Gelombang Dua Dimensi
Kinematika gelombang dua dimensi dapat dihitung menggunakan Teori Gelombang
Stream Function dengan diketahuinya apparent wave period Tapp, ketinggian
gelombang H ,kedalaman saat badai d.
Dalam banyak kasus, teori gelombang Stokes orde ke-5 akan menghasilkan
keakuratan hasil yang dapat diterima. Gambar 2.6 menunjukkan daerah aplikasi dari
Stokes orde ke-5 dan berbagai derajat dari penyelesaian Stream Function pada bidang
H/gTapp2,d/gTapp2.
Nina Purnamasari (15004005)
Joni Wahyudi (15004045)
II-18
BAB II TINJAUAN PUSTAKA
Gambar 2.13 Diagram Penentuan Teori Gelombang Aplikasi
2.2.4.6
Faktor Kinematika Gelombang
Kinematika gelombang umum dua dimensi dari teori gelombang Stream Function
atau Stokes orde ke-5 tidak memperhitungkan penyebaran arah gelombang atau
ketidakseragaman dalam bentuk profil gelombang. Karakteristik nyata ini dapat
dimodelkan dalam analisis gelombang deterministik dengan mengalikan kecepatan
dan percepatan mendatar dari penyelesaian gelombang dua dimensi umum dengan
faktor kinematika gelombang. Pengukuran kinematika gelombang memiliki faktor
berkisar antara 0,85 sampai 0,95 untuk badai tropis dan 0,95 sampai 1,0 untuk badai
bukan tropis.
2.2.4.7
Marine Growth
Nina Purnamasari (15004005)
Joni Wahyudi (15004045)
II-19
BAB II TINJAUAN PUSTAKA
Semua bagian dari struktur (elemen, konduktor, riser, struktur tambahan, dan lainlain) yang berada dibawah permukaan laut tertinggi, luas penampangnya diperbesar
dikarenakan adanya marine growth. Diameter efektif dari elemen adalah D = Dc + 2t,
dimana Dc adalah diameter luar dan t adalah ketebalan marine growth rata-rata yang
dapat diperoleh dari pengukuran keliling dengan pita pengukur.
2.2.4.8
Koefisien Hidrodinamik
Pembebanan pada struktur yang diakibatkan oleh gelombang merupakan hasil dari
daerah tekanan yang dihasilkan oleh gelombang. Beberapa mekanisme terpisah telah
diidentifikasikan dalam kejadian ini.
Terdapat komponen gaya seret yang bersesuaian dengan daerah terpaan dari badan
struktur dan kuadrat dari kecepatan arus. Hal ini muncul dari gangguan arus akibat
badan struktur. Gaya inersia terdiri dari dua komponen, yaitu gaya yang seharusnya
bekerja pada massa air yang telah digantikan oleh badan struktur, atau gaya FroudeKrylof, dan gaya yang bekerja pada massa air yang ditahan oleh badan struktur atau
disebut gaya massa tambahan. Beberapa faktor yang mempengaruhi besar dari gaya
seret adalah koefisien, CD, dan ukuran dari elemen, A, atau dalam kasus ini yang
merupakan obyek silinder adalah diameter elemen, D. Dan beberapa faktor yang
mempengaruhi besar gaya inersia adalah koefisien inersia, CM, dan volume yang
dipindahkan elemen, V.
Untuk situasi desain biasa, gaya gelombang global dapat diperhitungkan dengan
menggunakan nilai-nilai berikut ini, untuk silinder yang tidak tertutup.
Halus
CD = 0.65
CM = 1.6
Kasar
CD = 1.05
CM = 1.2
Banyak bukti eksperimen telah menunjukkan bahwa nilai dari koefisien hidrodinamik
tidak tetap dan berubah mengikuti diameter elemen dan bilangan Reynolds. Tabel 2.5
memberikan nilai CD dan CM untuk berbagai diameter.
Tabel 2.5 Koefisien Hidrodinamik API
Nina Purnamasari (15004005)
Joni Wahyudi (15004045)
II-20
BAB II TINJAUAN PUSTAKA
2.2.4.9
Gaya Gelombang Pada Tiang Silinder Tegak
Gambar 2.14 Gaya Gelombang pada Tiang Silinder Tegak
Gaya pada tiang silinder tegak akibat gelombang pertama kali diperkenalkan oleh
Morison dengan batasan diameter tiang relatif kecil dibandingkan panjang gelombang
yang menerpa tiang.
keterangan:
πD 2
1
ρC d D U U + ρC m
ax
2
4
f
=
f
= gaya per satuan panjang
ρ
= kerapatan massa fluida
(2.30)
U = kecepatan partikel air pada kedalaman tertentu, tegak lurus
terhadap tiang
ax = percepatan partikel air pada kedalaman tertentu, tegak lurus
terhadap tiang
D = diameter tiang
Cm = koefisien inersia
Cd = koefisien seret
Nina Purnamasari (15004005)
Joni Wahyudi (15004045)
II-21
BAB II TINJAUAN PUSTAKA
Suku pertama dari ruas kanan pada persamaan Morison merupakan komponen gaya
seret (drag force) yang besarnya sebanding dengan kuadrat kecepatan partikel. Tanda
harga absolut digunakan untuk memastikan arah komponen gaya seret sesuai dengan
arah kecepatan partikel. Suku kedua dari ruas kanan merupakan komponen gaya
inersia yang besarnya sebanding dengan percepatan partikel air.
Modifikasi nilai koefisien seret dan inersia diperlukan apabila pada batang tubular
tersebut terdapat tambahan struktur atau komponen lain, misalnya anoda. Modifikasi
koefisien seret dan inersia tersebut ditentukan dengan rumusan sebagai berikut:
keterangan:
Cd’ =
A1C d 1 + nA2 C d 2
A1
(2.31)
Cm’=
V1C m1 + nV2 C m 2
V1
(2.32)
A1 = luas seret batang tubular
Cd1 = koefisien seret batang tubular
A2 = luas seret komponen / anoda
Cd2 = koefisien seret komponen / anoda
V1 = volume batang tubular
Cm1= koefisien massa batang tubular
V2 = volume komponen / anoda
Cm2= koefisien massa komponen / anoda
n
= jumlah komponen / anoda
Gaya total F diperoleh dengan cara mengintegrasikan persamaan Morison sepanjang
elemen struktur. Pada gambar silinder tegak diatas, gaya total dihitung dengan
mengintegrasikan persamaan Morison dari z = 0 sampai z = z.
z
F =
∫ f (z )dz
(2.33)
0
Dengan cara yang sama, momen total M pada z = 0 (sea floor) akibat gaya gelombang
yang bekerja sepanjang z = 0 sampai dengan z = z adalah,
z
M =
∫ zf (z )dz
(2.34)
0
Titik tangkap resultan gaya gelombang yang bekerja pada tiang silinder tegak
dihitung dengan persamaan
Nina Purnamasari (15004005)
Joni Wahyudi (15004045)
II-22
BAB II TINJAUAN PUSTAKA
z=
M
F
(2.35)
dimana z dihitung dari dasar tiang (sea floor)
2.2.4.10
Gaya Akibat Gelombang Linier (Airy)
Misalkan gelombang permukaan yang terjadi adalah gelombang linier dengan
parameter-parameter antara lain tinggi gelombang H, frekuensi gelombang ω,
bilangan gelombang k, dan kedalaman perairan h dengan mengambil x = 0 sebagai
posisi / lokasi tiang silinder, maka gaya total yang terjadi pada tiang tegak adalah,
F = FD + FI
(2.36)
dengan komponen gaya seret dari persamaan Morison,
FD =
ρC D D
32k
⎛
⎞
2kz
2kz
⎟⎟ cos ωt cos ωt
+
2
⎝ sinh kh sinh kh ⎠
(ωH )2 ⎜⎜ sinh 2
(2.37)
dan komponen gaya inersia akibat gelombang,
FI =
ρC I πD 2
2k
4
ω2H
sinh kz
sin ωt
sinh kh
(2.38)
Momen pada tiang di dasar perairan adalah,
M = MD + MI
(2.39)
dimana,
MD =
ρC D D
64k
2
(ωH )2 Q1 cos ωt cos ωt
ρC I πD 2
(2.40)
ω 2 HQ2 sin ωt
MI =
−
Q1 =
2kz sinh 2kz − cosh 2kz + 2(kz ) + 1
sinh 2 kh
(2.42)
Q2 =
kz sinh kz − cosh kz + 1
sinh kh
(2.43)
2k
2
4
(2.41)
2
2.2.4.11
Gaya Akibat Gelombang Stokes
Dengan memasukkan komponen kecepatan dan percepatan horisontal partikel air
gelombang Stokes pada persamaan Morison, maka gaya pada tiang silinder tegak (x =
0) menjadi,
Nina Purnamasari (15004005)
Joni Wahyudi (15004045)
II-23
BAB II TINJAUAN PUSTAKA
f=
ρC D D 2
2k 2
4 5− m
∑∑U
m =1 n =1
mωt cos nωt −
mU n cos
ρC I πDω
8k
5
∑R
n =1
n
sin nωt
(2.44)
dimana koefisien Un dan Rn didefinisikan pada persamaan 2.21 dan 2.25. Sesuai
dengan teori Stokes orde ke-5, perkalian UmUn untuk m+n > 5 diabaikan. Maka dari
persamaan 3.30 didapat,
F(z)
= FD(z) + FI(z)
FD
=
FI
ρC D Dω 2
2k 3
= -
4 5− m
∑∑ A
m =1 n =1
ρC I πD 2ω 2
4k 2
(2.45)
mn
5
∑B
n =1
n
cos mωt cos nωt (2.46)
sin nωt
(2.47)
Koefisien Amn (untuk m ≠ n) dan Ann (untuk m = n) adalah,
=
Gm Gn S m + nWm + n
S W
+ m−n m−n
2S m S n (m + n)Gm + n (m − n)Gm − n
(2.48)
Ann
=
Gn2 S 2 nW2 n kz
+
2
S n2 4nG2 n
(2.49)
Sn
= sin nkh
Wn
= koefisien kecepatan = Gn
Amn
(2.50)
sinh nkz
sinh nkh
(2.51)
Koefisien Bn adalah,
B1 = W1 -
1 G1G2 S 3
1 G 2 G3 S 5
W3 −
W5
6 G3 S 1 S 2
10 G5 S 2 S 3
1 G12
1 G1G3 S 4
kz −
W4
B2 = W2 2
2 S1
4 G 4 S1 S 3
B3 = W3 -
3 G2
3 G1G4 S 5
W1 −
W5
2 S2
10 G5 S1 S 4
B4 = W4 -
GG S
1 G22
kz − 1 3 2 W2
2
2 S2
G 2 S1 S 3
B5 = W5 -
5 G 2 G3 S1
5 G1G4 S 3
W1 −
W3
2 G1 S 2 S 3
6 G3 S 1 S 4
(2.52)
Karena bentuk persamaan yang komplek, perhitungan gaya dan momen maksimum
akan sulit dilakukan seperti pada perhitungan gaya akibat gelombang linier. Dalam
hal ini, lebih baik menggunakan metoda numerik dimana tiang silinder dibagi menjadi
N segmen dan menghitung gaya pada setiap segmen dengan menggunakan persamaan
Nina Purnamasari (15004005)
Joni Wahyudi (15004045)
II-24
BAB II TINJAUAN PUSTAKA
2.45 pada saat (t) gaya maksimum terjadi dan menganggap gaya yang terjadi merata
sepanjang tiap segmen. Momen pada dasar tiang bisa didapat dengan menjumlahkan
momen dari tiap segmen. Dengan menganggap gaya tersebut terdistribusi secara
merata, titik tangkap gaya resultan akan terletak ditengah setiap segmen sehingga
momen pada tiang di dasar perairan dapat dituliskan sebagai berikut,
M =
1
1
F1 z1 + (F2 − F1 )( z 2 + z1 )
2
2
(2.53)
Harga t harus dicari dimana gaya yang terjadi maksimum. Secara umum, momen yang
terjadi pada dasar tiang bila kita membagi tiang menjadi N segmen adalah,
M =
1 N
∑ (Fn − Fn−1 )(z n − z n−1 )
2 n =1
(2.54)
dengan F0 = 0 dan z0 = 0
2.2.4.12
Gaya Gelombang Pada Tiang Silinder Miring
Penerapan persamaan Morison pada tiang silinder miring dilakukan pada saat
menghitung gaya gelombang pada ”cross brcing” struktur atau pada kaki jacket yang
tidak tegak (battered). Chakrabarti dkk. (1975) mengembangkan metoda penerapan
persamaan Morison untuk menentukan gaya gelombang pada tiang miring dengan
menguraikan kecepatan dan percepatan partikel kedalam komponen tegak lurus dan
sejajar / tangensial sumbu tiang silinder. Kemudian, hanya komponen kecepatan dan
percepatan partikel yang tegak lurus tiang silinder yang digunakan untuk menentukan
gaya per satuan panjang pada tiang silinder miring.
Arah gaya yang bekerja adalah tegak lurus terhadap sumbu tiang dan sesuai dengan
arah komponen kecepatan dan percepatan partikel tegak lurus sumbu tiang silinder
miring. Untuk keperluan analisa struktur, gaya tersebut bisa disesuaikan lagi kedalam
komponen gaya vertikal dan gaya horisontal.
Perhatikan tiang miring pada gambar 2.8. Misalkan gelombang bergerak dalam arah
sumbu +x, sehingga terdapat komponen horisontal dan vertikal kecepatan (u dan v)
dan percepatan (ax dan ay) partikel air akibat gelombang.
Nina Purnamasari (15004005)
Joni Wahyudi (15004045)
II-25
BAB II TINJAUAN PUSTAKA
Gambar 2.15 Tiang Silinder Miring
Dengan menggunakan sistem koordinat polar dan sudut θ dan β untuk mendefinisikan
orientasi dari sumbu tiang, besar kecepatan partikel arah tegak lurus / normal sumbu
tiang adalah,
Vn =
[u
2
+ v 2 − (c x u + c y v )
2
]
1
2
(2.55)
komponen kecepatan pada arah x, y dan z adalah sebagai berikut,
un = u – cx (cxu + cyv)
vn = v – cy (cxu + cyv)
(2.56)
wn = – cz (cxu + cyv)
dimana,
cx = sin β cos θ
cy = cos β
(2.57)
cz = sin β sin θ
Percepatan partikel arah normal sumbu tiang silinder dapat diuraikan kedalam
komponen dalam arah x, y dan z sebagai berikut,
anx = ax – cx (cxax + cyay)
any = ay – cy (cxax + cyay)
(2.58)
anz = - cz (cxax + cyay)
Maka komponen gaya per satuan panjang dalam arah x, y dan z adalah,
fx =
1
πD 2
ρC D DVn u n + ρC I
anx
2
4
Nina Purnamasari (15004005)
Joni Wahyudi (15004045)
II-26
BAB II TINJAUAN PUSTAKA
fy =
πD 2
1
ρC D DVn vn + ρC I
any
2
4
fz =
1
πD 2
ρC D DVn wn + ρC I
az
2
4
(2.59)
Arah gaya f disesuaikan dengan arah komponen gaya fx, fy dan fz.
Komponen total gaya yang bekerja pada tiang silinder miring harus dihitung dengan
cara integrasi numerik berdasarkan persamaan berikut,
Fx =
∫f
x
ds
∫f
y
ds
∫f
z
ds
s
Fy =
(2.60)
s
Fz =
s
dimana variabel s menunjukan integrasi sepanjang tiang silinder.
2.2.4.13
Prosedur Perhitungan Gaya Gelombang Pada Deck
Prosedur perhitungan gaya gelombang pada deck tergantung pada tinggi puncak
gelombang. Tinggi puncak gelombang harus dihitung menggunakan teori gelombang
berdasarkan section 2.3.1.b.2 API RP 2A-WSD (kinematika gelombang dua dimensi),
tinggi gelombang untuk analisis tegangan ultimat, periode gelombang, kondisi pasang
saat badai. Langkah-langkah perhitungan gaya pada deck sebagai berikut:
1.
Dari data tinggi puncak gelombang, hitung luas daerah tangkapan
gelombang pada deck (A), dengan arah gelombang yang terjadi (θw).
Luas daerah tangkapan gelombang pada deck berupa daerah arsiran pada
gambar 2.16, luas antara daerah scaffolding deck terbawah sampai equipment
tertinggi pada main deck. Luas daerah tangkapan untuk perhitungan gaya
padad deck adalah seluruh luasan susunan-susunan bagian deck tersebut
dengan tambahan ketinggian hingga di atas MLLW (Mean Lower Low Water)
yang merupakan jumlah dari kondisi pasang saat badai dan tinggi puncak
gelombang yang dibutuhkan untuk analisis tegangan ultimat.
Untuk penampang sub-cellar deck rangka ringan tanpa equipment dihitung
satu setengah kali luas daerah tangkapan gelombang pada seluruh luasan
tangkapan. Area deckleg dan bracing di atas cellar deck adalah bagian dari
Nina Purnamasari (15004005)
Joni Wahyudi (15004045)
II-27
BAB II TINJAUAN PUSTAKA
luas daerah tangkapan. Deckleg dan bracing yang berada di bawah cellar deck
harus dimodelkan bersama dengan member jacket dalam prosedur
perhitungan gaya pada jacket. Struktur rangka batang tambahan di atas
equipment pada main deck dapat diabaikan.
Berikut ini adalah rumus perhitungan area (A):
(2.61)
Keterangan:
θw, Ax, dan Ay ditentukan pada gambar 2.17
Gambar 2.16 Penentuan Luas Daerah Tangkapan
Nina Purnamasari (15004005)
Joni Wahyudi (15004045)
II-28
BAB II TINJAUAN PUSTAKA
Gambar 2.17 Sudut Datang Gelombang dan Ketentuan Arah
2.
Menggunakan teori gelombang berdasarkan section 2.3.1.b.1 API RP
2A-WSD dan menghitung maksimum kecepatan gelombang arah horizontal,
V, pada elevasi puncak gelombang atau main deck teratas, dicari nilai elevasi
terendah dari kedua elevasi tersebut.
3.
Gaya gelombang pada deck, Fdk dihitung sebagai berikut:
(2.62)
Keterangan:
U
= Kecepatan arus sejajar dengan gelombang
awkf = Faktor kinematik gelombang (0.88 untuk hurricane & 1 untuk
winterstorm)
αcbf = Current blockage factor untuk jacket
ρ
= Massa jenis air laut
Koefisien drag , Cd diberikan pada tabel C.17.6.2-1 API RP 2A-WSD.
Nina Purnamasari (15004005)
Joni Wahyudi (15004045)
II-29
BAB II TINJAUAN PUSTAKA
4.
Gaya Fdk diberikan pada elevasi Zdk di atas cellar deck terbawah. Zdk
ditentukan sebesar 50% jarak antara titik terendah luas daerah tangkapan dan
tinggi puncak gelombang terendah atau main deck teratas.
2.2.5
Arus
Arus, relatif memiliki pergerakan yang konstan. Arus di laut biasanya terjadi akibat
adanya pasang surut dan gesekan angin pada permukaan air (wind-drift current).
Kecepatan arus bekerja pada arah horisontal dan bervariasi menurut kedalaman. Besar
dan arah arus pasang surut dipermukaan biasanya ditentukan berdasarkan pengukuran
di lokasi. Wind-drift current di permukaan biasanya diasumsikan sekitar 1 % dari
kecepatan angin pada ketinggian 30 ft diatas permukaan air. Untuk kebutuhan
rekayasa, variasi arus pasang surut terhadap kedalaman biasanya diasumsikan
mengikuti profil pangkat 1/7 ("one-seventh power law") dan variasi arus akibat
gesekan angin diasumsikan linier terhadap kedalaman.
Variasi arus ditunjukkan pada Gambar 2.18.
Gambar 2.18 Variasi Arus
Dalam kondisi badai, arus terjadi bersamaan dengan gerakan air akibat gelombang.
Arah arus pasang surut bisa tidak sama dengan arah rambat gelombang, tetapi winddrift current biasanya diasumsikan searah dengan gerakan gelombang. Arus yang
terjadi bersamaan dengan gelombang akan mempengaruhi karakteristik gelombang.
Besar pengaruh arus terhadap gelombang tergantung pada rasio kecepatan maksimum
arus terhadap kecepatan gelombang. Namun pengaruh arus bisa diabaikan untuk
kondisi gelombang saat badai (storm). Sehingga untuk kebutuhan desain, dalam
perhitungan gaya akibat arus dan gelombang yang bekerja pada struktur dilakukan
dengan menambahkan kecepatan arus dengan kecepatan horisontal akibat gelombang.
Metoda ini sesuai dengan API RP2A-WSD yang ditunjukkan pada Gambar 2.12.
Nina Purnamasari (15004005)
Joni Wahyudi (15004045)
II-30
BAB II TINJAUAN PUSTAKA
2.2.5.1
Current Blockage Factor
Kecepatan arus disekitar anjungan berkurang akibat faktor hambatan (Current
Blockage Factor). Dengan kata lain, kehadiran struktur mengakibatkan arus
menyebar, sebagian arus mengelilingi struktur dan tidak melaluinya, dan kecepatan
arus disekitar struktur berkurang. Current Blockage Factor dihitung dengan
menggunakan persamaan berikut:
(C d D )i ⎤
⎡
+
1
∑
⎢
4W ⎥⎦
⎣
−1
(2.63)
Dimana Σ(CdD)i adalah penjumlahan dari “drag diameter” dari seluruh elemen yang
terpotong oleh suatu bidang mendatar tertentu dan W merupakan lebar keseluruhan
dari anjungan, tegak lurus terhadap arus pada elevasi tersebut.
2.2.5.2
Kinematika Gelombang dan Arus Gabungan
Kinematika gelombang yang telah disesuaikan dengan penyebaran arah dan
ketidakseragaman, harus digabungkan dengan profil arus yang telah disesuaikan
dengan faktor hambatan. Karena profil arus hanya ditentukan untuk kedalaman air
rata-rata pada kriteria disain, harus digunakan beberapa cara untuk memperpanjang
atau memperpendek profil arus tersebut terhadap ketinggian gelombang lokal.
Untuk profil arus dimana perpanjangan linier merupakan pendekatan yang dapat
diterima, Vz arus pada jarak z diatas kedalaman laut rata-rata, dapat diperhitungkan
dari profil arus yang telah ditentukan pada elevasi z’ dengan menggunakan persamaan
di bawah ini:
Vx = Vz '
keterangan:
(z + d ) d
(z'+d ) (d + η )
(2.64)
Vz’ = arus tertentu pada elevasi z’
d
= kedalaman air pada saat badai
η = jarak antara permukaan gelombang dengan kedalaman laut
rata-rata
(η dan z positif diatas kedalaman laut rata-rata dan sebaliknya)
Nina Purnamasari (15004005)
Joni Wahyudi (15004045)
II-31
BAB II TINJAUAN PUSTAKA
Penelitian telah menunjukkan bahwa sebuah profil arus yang diperpanjang secara
non-linier cocok digabungkan dengan kinematika gelombang yang telah terpengaruh
Doppler. Perpanjangan non-linier memperhitungkan arus yang telah dipanjangkan,
Vz, untuk sebuah partikel yang berada pada elevasi z, berdasarkan kecepatan Vz’ yang
telah ditentukan di profil arus pada elevasi z’ sebagai berikut:
Vz = Vz’
z '+η ⎡ sinh(2π ( z '+ d ) / λm ) ⎤
⎢
⎥
z ⎣ sinh(2πd / λm ) ⎦
(2.65)
dimana λm adalah panjang gelombang untuk ketinggian H dan perioda Tapp tertentu.
2.2.6
Gaya Apung
Tekanan air pada struktur yang tenggelam, timbul karena berat air diatasnya dan
pergerakan fluida di sekitar struktur yang diakibatkan oleh gelombang. Tekanan air
pada struktur yang tenggelam dapat memperbesar tegangannya. Gaya yang
diakibatkan oleh gelombang telah dihitung di dalam persamaan Morison sedangkan
gaya apung yang diakibatkan oleh berat air diatasnya diperhitungkan dengan
menggunakan persamaan berikut:
Fb = γf V
keterangan:
(2.66)
γf = berat jenis fluida
V = volume struktur yang tenggelam
2.3
Kombinasi Pembebanan
Anjungan harus didesain dengan kombinasi pembebanan yang akan menghasilkan
efek yang paling membahayakan bagi struktur. Kombinasi pembebanan ini terdiri dari
beban lingkungan, beban mati dan beban hidup yang sesuai.
Beban lingkungan harus dikombinasikan dengan cara yang sesuai dengan
kemungkinan kejadian tersebut terjadi bersamaan selama kondisi pembebanan yang
sedang dipertimbangkan.
Pembagian beban yang akan dikombinasikan:
1.
Beban gravitasi
Beban gravitasi ini terdiri dari:
a. Berat sendiri platform .
b. Beban peralatan.
Nina Purnamasari (15004005)
Joni Wahyudi (15004045)
II-32
BAB II TINJAUAN PUSTAKA
c. Beban lain-lain (perubahan desain, perubahan fabrikasi, berat , dan
lain-lain).
2.
Beban angin
-
Dianalisis untuk kondisi operasional dan kondisi ekstrim.
-
Beban angin ini bekerja pada 12 mata angin. Setiap arahnya
diproyeksikan pada arah x dan arah y.
-
Koefisien untuk beban angin ini dibedakan berdasarkan arah angin
yang sedang ditinjau. Hal ini dilakukan agar desain yang dihasilkan
lebih akurat dan menyerupai kondisi sebenarnya.
-
Penting untuk diperhatikan formula yang akan dipakai dalam
analisis beban angin.
3.
Beban gelombang dan arus
-
Dianalisis untuk kondisi operasional dan kondisi ekstrim.
-
Dianalisis pada 12 mata angin.
-
Koefisien untuk beban gelombang dan arus diperoleh dari besarnya
Dynamic Amplification Factor
(DAF), yang nilainya sudah
diasumsikan sebelumnya. Besar DAF untuk kondisi operasional
dan ekstrim memiliki nilai yang berbeda.
Tiap elemen anjungan harus didesain dengan kombinasi pembebanan yang
mengakibatkan tegangan terbesar pada elemen, dengan turut mempertimbangkan
tegangan izin untuk kondisi pembebanan yang mengakibatkan tegangan tersebut.
Kombinasi pembebanan pada umumnya terbagi menjadi:
1.
Kombinasi pembebanan antara beban lingkungan, beban mati, dan
beban hidup maksimum saat operasi normal.
2.
Kombinasi pembebanan antara beban lingkungan, beban mati, dan
beban hidup minimum saat operasi normal.
3.
Kombinasi pembebanan antara beban lingkungan, beban mati, dan
beban hidup maksimum pada kondisi ekstrim.
4.
Kombinasi pembebanan antara beban lingkungan, beban mati, dan
beban hidup minimum pada kondisi ekstrim.
Adapun komponen penyusun dari kombinasi pembebanan:
a.
Komponen akibat beban gravitasi.
Nina Purnamasari (15004005)
Joni Wahyudi (15004045)
II-33
BAB II TINJAUAN PUSTAKA
Untuk kondisi operasional, beban gravitasi yang digunakan adalah
beban gravitasi maksimum, sedangkan untuk kondisi ekstrim, beban
gravitasi yang digunakan adalah beban gravitasi minimum.
b.
Komponen akibat beban angin yang sudah diproyeksikan pada arah x
dan arah y.
c.
Komponen akibat beban gelombang dan arus pada arah mata angin
yang sedang ditinjau.
2.4
Perencanaan Kekuatan Struktur Baja Tubular
Struktur lepas pantai biasanya menggunakan baja struktur biasa. Material baja akan
tetap bersifat elastis selama tegangan yang terjadi tidak melampaui tegangan leleh.
Tujuan utama dari desain adalah memiliki ukuran komponen yang sesuai, sehingga
kondisi elastis tetap dipenuhi selama di bebani beban rencana (design-level loading).
Faktor keamanan (safety factor) biasanya diterapkan untuk mendapatkan tegangan ijin
(allowable stress = yield stress / safety factor) yang kemudian dijadikan kriteria
tegangan yang tidak boleh dilewati selama struktur dibebani gaya rencana.
Filosofi perencanaan yang diterapkan dalam merancang fixed platform yang akan
dibahas dalam laporan ini adalah filosofi tegangan kerja / elastis (working stress
design —WSD). Menurut filosofi ini, elemen struktural
harus direncanakan
sedemikian rupa sehingga tegangan yang dihitung akibat beban kerja tidak melampaui
tegangan izin yang diberlakukan.
Tegangan izin ini ditentukan oleh peraturan bangunan atau spesifikasi (seperti dalam
AISC) untuk mendapatkan faktor keamanan terhadap tercapainya tegangan batas,
seperti tegangan leleh minimum atau tegangan buckling (tekuk). Tegangan yang
dihitung harus berada dalam batas elastis. Misalnya pada sebuah balok, kriteria aman
dalam perencanaan WSD bisa dinyatakan sebagai
(2.67)
Dengan fb adalah tegangan di serat terluar dari penampang balok akibat momen beban
kerja maksimum M yang dihitung dengan menganggap balok bersifat elastis, c adalah
jarak dari garis netral balok ke serat terluar, dan I adalah momen inersia penampang
balok. Tegangan izin Fb diperoleh dengan membagi tegangan batas (seperti tegangan
batas Fb atau tegangan tekuk Fcr) terhadap faktor keamanan.
Nina Purnamasari (15004005)
Joni Wahyudi (15004045)
II-34
BAB II TINJAUAN PUSTAKA
2.4.1
Batang Tarik
Batang tarik lazim dijumpai pada struktur baja sebagai member (batang) struktural
pada struktur rangka berjenis menara. Keadaan batas kekuatan yang berpengaruh bagi
suatu batang tarik dapat berupa (a) pelelehan penampang lintang bruto batang pada
tempat yang jauh dari titik sambungan dan () retakan dari suatu luas bersih efektif
(yakni melalui lubang-lubang) pada sambungan. Bila keadaan batasnya adalah
pelelehan umum dari penampang lintang bruto atas panjang batang, seperti halnya
untuk batang tarik tanpa pelubangan (dengan sambungan las), kekuatan batas Tu
dapat dinyatakan sebagai
(2.68)
dengan Ag adalah luas penampang bruto dan Fy adalah tegangan leleh baja. Beban
kerja yang aman T dapat dihitung dengan membagi kekuatan dengan faktor
keamanan, yaitu
(2.69)
Untuk batang silinder yang mengalami beban tarik, formula API RP 2A-WSD dalam
menentukan tegangan tarik ijin Ft dapat dituliskan sebagai berikut:
(2.70)
Batas tegangan ijin tersebut menerapkan angka keamanan sebesar 1,67.
2.4.2
Batang Tekan
Pada umumnya batang tekan akan mengalami buckling (tekuk) atau lenturan tibatiba akibat ketidakstabilan sebelum mencapai kekuatan penuh material baja tersebut.
Hanya batang yang sangat pendek saja yang dapat dibebani sampai ke tegangan
lelehnya. Karena itu diperlukan pengetahuan yang mendalam tentang stabilitas batang
tekan untuk desain batang tekan dalam struktur baja.
2.4.2.1
Tekuk Kolom dan Tekuk Lokal
Berdasarkan API RP 2A-WSD, untuk elemen dengan rasio D/t kurang dari atau sama
dengan 60, tegangan tekan izin, Fa, harus dihitung dengan persamaan AISC berikut:
(2.71)
Nina Purnamasari (15004005)
Joni Wahyudi (15004045)
II-35
BAB II TINJAUAN PUSTAKA
(2.72)
dimana:
(2.73)
E = Modulus Elastisitas Young, ksi (MPa)
K = faktor panjang efektif
L = panjang batang tak tersokong (unbraced), in. (m)
r
= radius girasi, in. (m)
Untuk elemen dengan rasio 60 < D/t ≤ 300 dan tebal silinder t ≥ 0,25 in (6 mm), ganti
tegangan tekuk lokal kritis (Fxe dan Fxc diambil yang lebih kecil) untuk Fy dalam
menentukan Cc dan Fa. Rumus Fxe atau Fxc diberikan sebagai berikut:
•
Tegangan Tekuk Lokal Elastis, Fxe
(2.74)
Secara teoritis, nilai C = 0,6. Namun demikian, reduksi nilai C = 0,3 diizinkan untuk
memperhitungkan pengaruh ketidaksempurnaan geometrik.
•
Tegangan Tekuk Lokal Inelastis, Fxc
(2.75)
2.4.2.2
Panjang Efektif
Pembahasan mengenai kekuatan batang tekan di atas menggunakan batang dengan
tumpuan sendi pada kedua ujungnya sehingga tidak ada kekangan rotasional atau
momen pada kedua ujung batang tersebut. Untuk batang tekan atau kolom dengan
ujung tumpuan sendi, panjang ekivalennya Kl adalah sama dengan panjang l. Maka
dalam hal ini harga K adalah 1,0. Panjang ekivalen batang tekan dengan ujung
tumpuan sendi disebut sebagai panjang efektif dan K disebut sebagai faktor panjang
efektif.
Untuk kondisi struktur pada umumnya, terjadi kekangan momen pada ujung-ujung
batang tekan atau kolom sehingga menyebabkan titik momen nol atau titik balik
Nina Purnamasari (15004005)
Joni Wahyudi (15004045)
II-36
BAB II TINJAUAN PUSTAKA
(inflection point) bergerak menjauhi ujung-ujung yang ditahan. Kondisi ini bisa
dilihat pada Gambar 2.11, dimana panjang efektif Kl tereduksi.
Penilaian secara tepat mengenai derajat kekangan momen pada struktur pada
umumnya sangat sulit atau bahkan tidak mungkin. Kekangan momen tersebut
dipengaruhi oleh batang-batang yang tidak berdekatan yang mengikat ke batang tekan
atau kolom, oleh pondasi setempat dan lapisan tanah di bawahnya, dan interaksi
penuh semua batang dalam struktur rangka baja.
Gambar 2.19 Faktor Panjang Efektif
Tabel 2.6 Faktor Panjang Efektif
Situasi
Kaki Struktur Atas
Terkekang
Portal (tak terkekang)
Tiang dan Kaki Platform
Penampang Komposit
Kaki Platform Ungrouted
Tiang Pancang Ungrouted
Elemen Web Penopang Deck
Aksi In-Place
Nina Purnamasari (15004005)
Joni Wahyudi (15004045)
Faktor
Panjang
Efektif
(K)
Faktor
Reduksi (Cm)
1,0
K
(a)
(a)
1,0
1,0
1,0
(c)
(c)
(b)
0,8
(b)
II-37
BAB II TINJAUAN PUSTAKA
Aksi Out-of-Place
Penguat Brace
Panjang Face-toFace dari
Diagonal Utama
Untuk K Brace
Segmen lebih panjang dari
X Brace
Secondary Horizontal
Elemen Penghubung Penopang Deck
1,0
(a) atau (b)
0,8
(a) atau (b)
0,8
(c)
0,9
0,7
1,0
(c)
(c)
(a), (b) atau (c)
Nilai Faktor reduksi Cm ditujukan untuk tabel 2.6, adapun penjelasan notasi pada
Tabel 2.6 adalah:
(a)
0,85
(b)
0,6-0,4
, tetapi tidak boleh kurang dari 0,4 dan tidak boleh lebih
dari 0,85
(c)
2.4.3
1-0,4
, atau 0,85, yang manapun lebih kecil
Tegangan Lentur
Tegangan lentur izin, Fb, harus dihitung dengan menggunakan persamaan:
(2.76)
(2.77)
(2.78)
2.4.4
Kombinasi Beban Lentur dan Aksial
Hampir semua batang dalam sebuah struktur terkena momen lentur dan beban aksial
(tarik atau tekan) sekaligus. Gaya tekan aksial akan menambah momen lentur yang
besarnya sama dengan gaya tekan aksial dikali defleksi. Berikut adalah beberapa
Nina Purnamasari (15004005)
Joni Wahyudi (15004045)
II-38
BAB II TINJAUAN PUSTAKA
kemungkinan kombinasi beban aksial dan lentur, serta beberapa kecenderungan
model kegagalannya.
a.
Tarik aksial dan lentur. Biasanya gagal karena leleh.
b.
Tekan aksial dan lentur. Biasanya gagal karena tekuk pada bidang
lentur.
c.
Tekan aksial dan lentur bi-aksial pada penampang yang kaku terhadap
puntir. Biasanya gagal karena tekuk pada salah satu arah utama.
2.4.4.1
Kombinasi Tekan Aksial dan Lentur
Berdasarkan API RP 2A-WSD, dalam mendesain suatu batang tubular yang dikenai
kombinasi tekan dan lentur harus memenuhi persyaratan berikut:
(2.79)
Apabila
, maka persamaan inilah yang digunakan menggantikan kedua
persamaan di atas:
(2.80)
Persamaan tersebut mengasumsikan kalau nilai yang sama dari Cm dan Fe sesuai
untuk fbx dan fbx. Jika nilai lain dapat diterapkan, maka persamaan berikutlah yang
digunakan menggantikan persamaan sebelumnya:
(2.81)
Parameter yang digunakan dalam persamaan di atas adalah sebagai berikut:
Fa = tegangan izin aksial
Fb = tegangan izin terhadap momen
fa = tegangan aksial yang terjadi
fb = tegangan yang terjadi akibat lentur
Cm = faktor reduksi / pembesaran momen yang berkaitan dengan
kekangan`ujung
Nina Purnamasari (15004005)
Joni Wahyudi (15004045)
II-39
BAB II TINJAUAN PUSTAKA
Fe’ = Euler buckling stress
2.4.4.2
Kombinasi Tarik Aksial dan Lentur
Batang ubular yang dikenai kombinasi tarik aksial dan lentur, berdasarkan API RP
2A-WSD harus memenuhi persamaan berikut:
(2.82)
Komponen dari persamaan di atas harus dientukan berdasarkan kondisi tarik pada
batang tubular.
2.4.5
Tarik Aksial dan Tekanan Hidrostatis
Pada saat tegangan regangan elemen longitudinal dan keruntuhan terjadi bersamaan,
persamaan interaksi berikut di bawah ini harus dipenuhi:
(2.83)
dimana:
A harus dapat menunjukkan kombinasi regangan maksimum
v
= rasio Poisson = 0,3
Fy
= kuat leleh, ksi (MPa)
fa
= nilai absolut untuk tegangan aksial, ksi (MPa)
fb
= nilai absolut untuk yang diakibatkan oleh tegangan lentur, ksi (MPa)
fh
= nilai absolut untuk tegangan tekan, ksi (MPa)
Fhc
= tegangan hoop kritis
2.4.6
Tekan Aksial dan Tekanan Hidrostatis
Pada saat tegangan tekan longitudinal dan tegangan tekan hoop terjadi bersamaan,
maka persamaan di bawah ini harus dipenuhi:
(2.84)
Nina Purnamasari (15004005)
Joni Wahyudi (15004045)
II-40
BAB II TINJAUAN PUSTAKA
Persamaan di atas seharusnya menunjukkan kombinasi tegangan tekan terbesar. Pada
saat fx > 0,5 Fha, persamaan ini harus terpenuhi:
(2.85)
dimana:
SFx = faktor keamanan untuk tekan aksial
SFh = faktor keamanan untuk lentur
fx = fa + fb + (0,5fh), fx seharusnya menunjukkan kombinasi tegangan
tekan maksimum
Fxe = 2CE t/D
Fxc = Fy [1,64-0,23(D/t)1/4] ≤ Fxe
Fxc =Fy jika (D/t) ≤ 60
2.5
Sambungan Baja Tubular
2.5.1
Klasifikasi Sambungan
Klasifikasi sambungan sebagai K, T & Y, atau X harus diaplikasikan pada setiap
sambungan berdasarkan pola pembebanan untuk tiap-tiap kondisi pembebanan. Untuk
dapat dianggap sebagai sambungan tipe K, punching load pada brace harus
diseimbangkan oleh punching load pada brace di seberang sambungan pada bidang
yang sama. Untuk sambungan T & Y, punching load didekati sebagai gaya geser
balok di chord . Untuk sambungan X, punching load diteruskan melalui chord ke
brace
di seberang. Untuk brace yang meneruskan sebagian bebannya sebagai
sambungan K dan sebagian sebagai sambungan T & Y atau sambungan X,
interpolasikan berdasarkan masing-masing bagian secara keseluruhan.
Nina Purnamasari (15004005)
Joni Wahyudi (15004045)
II-41
BAB II TINJAUAN PUSTAKA
Gambar 2.20 Contoh Sambungan Tubular
Kekuatan dari sambungan dapat ditentukan berdasarkan punching shear atau nominal
loads pada brace.
2.5.2
Punching Shear
Kapasitas sambungan dihitung berdasarkan punching shear atau beban nominal pada
brace. Berikut ini adalah ilustrasi parameter-parameter sambungan.
Gambar 2.21 Sambungan Tubular Sederhana
Nina Purnamasari (15004005)
Joni Wahyudi (15004045)
II-42
BAB II TINJAUAN PUSTAKA
θ
= Sudut brace (dari chord)
g
= Jarak renggang, in. (mm)
t
= Ketebalan brace, in. (mm)
T = Ketebalan chord, in. (mm)
D = Diameter brace, in. (mm)
Selain itu ada juga parameter lain yang didapatkan dari parameter-parameter diatas,
yaitu:
Punching shear yang bekerja dihitung dengan persamaan:
(2.86)
dimana:
f
= tegangan aksial nominal (fx), lentur in-plane (fbz), atau lentur outof-plane (fby) pada brace (punching shear untuk masing-masing
dipisahkan)
τ
= ketebalan brace/chord
θ
= sudut brace
Tegangan izin punching shear, vpa, diperhitungkan terpisah untuk setiap komponen
dari pembebanan brace dan tipe penyaluran pembebanan (K, X, T & Y)
menggunakan faktor Qq dan Qf. Tegangan izin dipilih yang terkecil antara tegangan
izin AISC (0,4Fy) atau:
(2.87)
(peningkatan 1/3 jika memungkinkan)
dimana:
Fyc
= kekuatan leleh dari member chord pada sambungan (atau 2/3 dari
kekuatan tarik jika lebih kecil)
γ
= diameter chord/(2*ketebalan chord)
Qq
= faktor yang memperhitungkan tipe pembebanan dan geometri
Qf
= faktor yang memperhitungkan tegangan memanjang dari chord
(2.88)
(2.89)
Nina Purnamasari (15004005)
Joni Wahyudi (15004045)
II-43
BAB II TINJAUAN PUSTAKA
dimana:
λ
= 0,030 untuk tegangan aksial brace (fax)
= 0,045 untuk tegangan lentur in-plane (fbz)
= 0,021 untuk tegangan lentur out-of-plane (fby)
fAX, fIPB, fOPB adalah tegangan nominal aksial lentur in-plane, dan lentur out-of-plane
B
pada chord.
(Catatan: Qf = 1,0 apabila tegangan serat paling ekstrim dari chord adalah tegangan
tarik.)
Gambar 2.22 Ilustrasi Beban Aksial, Lentur In-Plane dan Lentur Out-of-Plane
Tegangan izin rata-rata (weighted average allowable stress) diperhitungkan
berdasarkan tipe sambungan untuk setiap kombinasi pembebanan.
Nilai-nilai untuk Qq:
untuk β > 0,6
Qβ =0,3/[β*(1-0,833β)]
untuk β ≤ 0,6
Qβ =1,0
untuk γ ≤ 20
Qβ =1,8-0,1 g/T
≥1
untuk γ > 20
Qβ =1,8-4 g/D
≥1
Tabel 2.7 Faktor Pengaruh Tipe Pembebanan dan Geometri
Tipe &
Tipe Pembebanan Brace
Geometri
Tarik
Tekan
Koverlap
1,8
1,8
K gap
(1,1+0,2/β)Qg (1,1+0,2/β)Qg
T&Y
1,1+0,2/β
1,1+0,2/β
X
1,1+0,2/β
(0,75+0,2/β)Qβ
1,1+0,2/β
1,1+0,2/β
X dgn
diafragma
Nina Purnamasari (15004005)
Joni Wahyudi (15004045)
Lentur IP
Lentur OP
3,72+0,67/β (3,72+0,67/β)Qβ
II-44
BAB II TINJAUAN PUSTAKA
Persamaan interksi berikut ini yang diperiksa untuk kombinasi tegangan aksial dan
lentur:
(2.90)
(2.91)
(catatan :arcsin dalam radian)
2.5.3
Penyaluran Beban Melewati Chord
Sambungan dimana bebannya disalurkan melewati chord dapat diperiksa untuk
keruntuhan umum sesuai rekomendasi API RP 2A-WSD. Untuk sambungan yang
diperkuat dengan meningkatkan ketebalan dan memiliki rasio diameter chord brace
kurang dari 0,9 beban cabang aksial izin (allowable axial branch load) dihitung dari
persamaan:
(2.93)
dimana:
P(1)
= kapasitas brace izin dengan menggunakan ketebalan elemen chord
nominal
P(2)
2.5.4
= kapasitas brace izin dengan menggunakan ketebalan sambungan
Diagram Alir Perhitungan Rasio Kekuatan Sambungan
Prosedur perhitungan rasio kekuatan joint punching shear dilakukan berdasarkan API
RP 2A-WSD dan ditunjukkan pada Gambar 2.16, Gambar 2.17, dan Gambar 2.18.
Nina Purnamasari (15004005)
Joni Wahyudi (15004045)
II-45
BAB II TINJAUAN PUSTAKA
Data:
1. Karakteristik Chord & Brace
-Diameter (D,d)
-Thickness (T,t)
2.Yield stress
3.Gap
Data:
1. Acting Punching Shear Stress
-Chord
-Brace (Vpa, Vob,Vib)
2.Faktor Lengkungan
- Chord
AWAL PERHITUNGAN Qq
PERHITUNGAN Qβ
TIDAK
YA
β>0,6
Qβ = 1
Qβ =
0,3
β (1 − 0,833β )
PERHITUNGAN Qg
YA
TIDAK
γ ≤ 20
Qg = 1,8-0,1g/T
Qg = 1,8-4g/D
MENGHITUNG Qq
AKSIAL Qq
LENTUR IN-PLANE Qq
LENTUR OUT-OF-PLANE Qq
1
2
3
Gambar 2.23 Diagram Alir Perhitungan Rasio Kekuatan Joint Punching Shear
Stress (bagian 1)
Nina Purnamasari (15004005)
Joni Wahyudi (15004045)
II-46
BAB II TINJAUAN PUSTAKA
Gambar 2.24 Diagram Alir Perhitungan Rasio Kekuatan Joint Punching Shear
Stress (bagian 2)
Nina Purnamasari (15004005)
Joni Wahyudi (15004045)
II-47
BAB II TINJAUAN PUSTAKA
2
2
2
f AX
+ f IPB
+ f OPB
A=
0 ,6 f yc
v pa = Q q .Q f .
⎛ Vp
⎜
⎜v
⎝ pa
Vp
v pa
0 ,6 γ
2
⎞
⎛ Vp
⎟
+⎜
⎟
⎜
⎠ IPB ⎝ v pa
2
⎞
⎟
⎟
⎠ OPB
2
2
⎛ Vp ⎞
⎛V ⎞
⎟ +⎜ p ⎟
+ arcsin ⎜
⎜v ⎟
⎜
⎟
π
⎝ pa ⎠ IPB ⎝ v pa ⎠ OPB
2
AX
F yc
Gambar 2.25 Diagram Alir Perhitungan Rasio Kekuatan Joint Punching Shear
Stress (bagian 3)
Nina Purnamasari (15004005)
Joni Wahyudi (15004045)
II-48
BAB II TINJAUAN PUSTAKA
2.6
Teori Pushover
Kejadian leleh pertama pada titik tekanan tertinggi pada komponen struktur sering
dijadikan ukuran kapasitas struktur. Banyak komponen yang mengalami hal ini
berulang-ulang. Komponen ini mampu menyalurkan ulang tegangan dan beban-beban
pada penampang saat beberapa bagian mulai untuk leleh. Pada kasus seperti ini, leleh
pertama merupakan kriteria konservatif. Salah satu contoh yang untuk transisi ini dari
leleh fiber pertama hingga kondisi plastis penuh pada balok akibat momen. Jika
penampang dikenakan kombinasi beban-beban misal, gaya aksial dan momen, maka
penyaluran ulang beban terjadi di antara keduanya. Hal ini sangat penting karena
disipasi energi menjadi terpusat dibandingkan tahanan maksimum.
Gambar 2.26 Definisi Kapasitas Ultimate
(Analisis Non-linear Offshore Platform, Jorgen Amdahl)
2.6.1
Kriteria Assessment dengan Analisis Non-Linier
Menurut API RP 2A-LRFD, kriteria perencanaan non-linier untuk analisis pushover
menggunakan parameter Reserve Strength Ratio (RSR). Dalam menilai kemampuan
struktur untuk menahan beban-beban berlebih pada beban rencana atau untuk
menyokong beban dalam keadaan dibutuhkan, beberapa pengukuran atas kemampuan
ini membutuhkan kekuatan cadangan.
Kekuatan cadangan biasanya didefinisikan sebagai kemampuan struktur untuk
menahan beban-beban berlebih pada perencanaan (Billington 1993). Tahanan
cadangan muncul saat tingkat komponen dimana terdapat ketaktentuan pada tahanan
Nina Purnamasari (15004005)
Joni Wahyudi (15004045)
II-49
BAB II TINJAUAN PUSTAKA
komponen dan komponen yang dikenakan pembebanan. Berdasarkan data statistik,
nilai karakteristik diadopsi untuk memastikan bahwa kemungkinan kegagalan dapat
diterima. Di luar hal tersebut, faktor keamanan diaplikasikan untuk meningkatkan
kepastian bertahan dan untuk menerima faktor-faktor untuk hal-hal yang tidak ada
pada data statistik. Sudah jelas bahwa kapasitas aktual komponen mampu melampaui
beban-beban yang yang diizinkan pada komponen dimana beban tersebut
direncanakan.
Pada tingkat sistem, bagaimanapun terdapat tambahan sumber tahanan cadangan.
Kegagalan salah satu komponen tidak membatasi kapasitas seluruh struktur
melainkan terdapat redundansi dan daktilitas yang cukup seperti beban-beban yang
bisa disalurkan ulang. Untuk struktur yang lebih rumit, kejadian kegagalan komponen
mungkin dibutuhkan sebelum kondisi ultimate dicapai. Kapasitas elastis rencana
dibatasi oleh teori kejadian kegagalan komponen pertama sehingga Reserve Strength
Ratio (RSR) dapat ditetapkan sebagai berikut:
(2.94)
Hal ini sama dengan faktor tahanan ekivalen kekuatan cadangan (Resistance
Equivalent Factor / REF) yang didefinisikan oleh Llyod dan Clawson (1984) sebagai
berikut:
(2.95)
Kriteria yang bisa diterima berdasarkan API RP 2A-LRFD Section R.5.2 harus
melebihi 1,6.
Pada literatur, RSR diukur sebagai variasi cara dan selain dari rasio beban yang
menyebabkan keruntuhan pada beban rencana. RSR juga dikutip sebagai istilah geser
dasar pada platform atau disebut sebagai overtunning momen. Pengukuran semacam
RSR dapat membimbing dalam kesulitan membandingkan konfigurasi struktur
alternatif yang memiliki geser dasa atau overtunning momen yang berbeda-beda
untuk kasus beban yang diberikan. Oleh karena itu, pendekatan yang lebih konsisten
adalah menggunakan rasio terhadap pembebanan yang diaplikasikan menurut Lllyod
dan Clawson (1984). Diketahui juga bahwa terdapat RSR yang terpisah untuk tiap
kasus atau kombinasi beban. Tentu saja pada kebanyakan kasus beban yang
menghasilkan utilisasi komponen terbesar pada tingkat beban rencana bukan
merupakan kasus pembebanan yang menghasilkan RSR terendah. Oleh karena itu,
Nina Purnamasari (15004005)
Joni Wahyudi (15004045)
II-50
BAB II TINJAUAN PUSTAKA
seperti yang diilustrasikan nanti, saat menilai RSR maka variasi penuh dari kasus
pembebanan harus dipertimbangkan untuk memastikan kasus paling kritis dapat
teridentifikasi.
Nina Purnamasari (15004005)
Joni Wahyudi (15004045)
II-51