KERAPATAN FLUKS LISTRIK

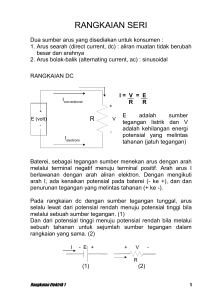
BAB V
ENERGI DAN POTENSIAL
4.1
Energi yang diperlukan menggerakan muatan titik dalam medan listrik.
Intensitas medan listrik didefinisikan sebagai gaya yang bertumpu pada
muatan uji satuan pada titik yang ingin kita dapatkan harga medan vektornya.
Jika muatan uji tersebut digerakkan melawan medan listrik, maka harus ada
gaya yang sama besar yang arahnya berlawanan dengan gaya medan. Karena
itu diperlukan energi atau kerja.
Misalkan pemindahan muatan Q sejarak dL dalam
E
medan listrik E. Gaya pada Q yang ditimbulkan oleh
F
medan listrik E adalah
Q
F = QE
Fa
Komponen gaya ini dalam arah dL
F = F.aL = QE.aL
Gaya lain Fa yang harus diterapkan yang sama besar gaya yg ditimbulkan
medan tapi berlawan arah adalah
Fa = -QE.aL
Energi yang harus disediakan sama dengan perkalian gaya dengan jaraknya
dW = Fa.dL
dW = -QE. aLdL
dW = -QE.dL
Kerja yang diperlukan untuk memindahkan muatan ke tempat yang jaraknya
tak berhingga harus ditentukan dengan mengintegrasikan,
akhir
W  Q  E.dL
awal
1
4.2
Integral Garis
Dalam sistem koordinat dL adalah:
dL = dxax + dyay + dzaz
dL = drar + rda + dzaz
dL = drar + rda + rsinda
(kartesian)
(silinder/tabung)
(bola)
Misalkan medan tak serbasama E = yax + xay + 2az. Kerja yang diperlukan
untuk membawa muatan 2 C dari B(1,0,1) ke A(0,8; 0,6;1) sepanjang busur
lingkaran yang pendek dari lingkaran x2 + y2 = 1
z=1
Dengan memakai integral kartesian, lintasan dL = dxa x + dyay + dzaz,
integralnya adalah,
A

W  Q E.dL
B
A
 2 ( ya x  xa y  2az ).(dxa x  dya y  dzaz )
B
0 ,8
0, 6
1
1
0
1
 2  ydx  2  xdy  4 dz
Dengan memakai persamaan lintasan lingkaran
W
 x 1  x 2  sin 1 x  y 1  y 2  sin 1 y
0 ,8
0, 6
1
0
0 ,8
0, 6
1
0
 2  1  x 2 dx  2  1  y 2 dy  0
= -(0,48 + 0,927 – 0 – 1,571) – (0,48 + 0,644 – 0 – 0)
= - 0,96 J
Jika dipilih lintasan garis lurus dari B ke A, maka harus terlebih dahulu
ditentukan persamaan garis lurusnya:
Ada tiga persamaan bidang yang dapat dilalui oleh garis:
2
y  yB 
yA  yB
(x  x B )
xA  xB
z  zB 
z A z B
(y  y B )
yA  yB
x  xB 
x A x B
(z  z B )
zA  zB
Dari tiga persamaan tersebut ada 2 persamaan yang dapat dipakai untuk
mendefinisikan persoalan tsb.
Dari persamaan pertama dapat didapatkan
y = -3(x-1)
Dari persamaan kedua didapatkan
z= 1
Jadi
0 ,8

0, 6
1


0
1
W  2 ydx  2 xdy  4 dz
1
0 ,8
0, 6
y
 6  ( x  1)dx  2  (1  )dy
3
1
0
 - 0,96 J
Contoh 1:
Hitunglah usaha yang dilakukan untuk memindahkan suatu muatan +2 C dari
(2,0,0) m ke (0,2,0) m melalui lintasan garis lurus penghubung kedua titik itu
di dalam medan listrik
E = 2x ax - 4y ay
(V/m)
Usaha diferensiasi
dW = -QE.dL
dW = -2(2x ax - 4y ay ).(dxax + dyay + dzaz)
= - 4xdx + 8y dy
3
Persamaan lintasan adalah x + y = 2, dimana dy = - dx sepanjang lintasan itu
dW = -4xdx + 8(2-x)(-dx) = (4x – 16)dx
0
W   (4x  16)dx = 24 J
2
Contoh 2
Lintasan muatan di dekat sebuah muatan garis tak terhingga dengan medan
yang arahnya radial E = Ea =
L
a
2 o 
Kerja yang diperlukan untuk membawa muatan positip Q melintasi lingkaran
dengan jari-jari 1. Unsur diferensial dL dipilih koordinat tabung dL = 1da
Muatan garis
tak terhingga L
L
a  .lda
2


o 1
awal
akhir
W  Q

1
2
L
da  .a1
2

o
0
 Q 
dL = l da
= 0
Muatan bergerak dari  = a ke  = a sepanjang
lintasan radial dL = d a
2
L
da .a1
2 o
0
L
W  Q 
 L d
2 o  
a
b
a
 Q 

dL= da
Q L b
ln
2 o a
4
b
DEFINISI BEDA POTENSIAL DAN POTENSIAL
Beda potensial (V) didefinisikan sebagai kerja (sumber luar) untuk
memindahkan satu satuan muatan positip dari suatu titik ke titik lain dalam
medan listrik.
akhir
Beda potensial = V =
 E.dL
awal
Beda potensial diukur dalam joule per coulomb, yang didefinisikan juga
sebagai Volt, yang lebih biasa dipakai disingkat sebagai V.
Jadi beda potensial antara titik A dan B adalah:
A
VAB    E.dL
B
Potensial titik A terhadap titik B didefinisikan sebagai usaha (kerja) yang
dilakukan dalam memindahkan suatu satuan muatan positip Q dari B ke A.
A
VAB
W

   E.dL
Q
B
(J/C atau Volt)
Jadi
Potensial di titik A adalah VA
Potensial di titik B adalah VB
Maka
VAB = VA - VB
Berdasarkan definisi tsb dipakai mencari beda potensial antara titik A dan B
pada jarak rA dan rB dari muatan titik Q dengan kedudukan di titik asal,
E  Era r 
Q
4 o r 2
ar
dL = drar
diperoleh
5
A
rA
B
2
rB 4 o r
VAB    E.dL   

Q
dr
Q 1 1
  
4 o  rA rB 
Jika rB > rA, beda potensial VAB menjadi positip yang menunjukkan bahwa
diperlukan energi oleh sumber luar untuk membawa muatan dari rB ke rA.
Apabila titik B ke tak terhingga
Va 
VA 
atau
Q
4 o
(
1 1
Q
1 1
 )
(  )
rA rB
4 o rA 
Q
4 o rA
V
atau
Q
4 o r
MEDAN POTENSIAL SISTEM MUATAN
Medan potensial sebuah muatan titik bermuatan Q1 pada titik r1 hanya
berhubungan dengan jarak r – r1dari Q1 ke titik r tempat potensial tersebut
dicari. Untuk acuan nol di tak terhingga, diperoleh
V(r ) 
Q1
4 o r  r1
Potensial yang ditimbulkan oleh 2 muatan Q1 di r1 dan Q2 di r2 merupakan
fungsi dari r – r1 dan r – r2yang masing-masing merupakan jarak dari
Q1 dan Q2 ke titik medan,
V( r ) 
Q1
Q2

4 o r  r1 4 o r  r2
Jika muatan terus bertambah, potensial yang ditimbulkan oleh n muatan titik
adalah,
V( r ) 
Q1
Q2
Qn

 ........... 
4 o r  r1 4 o r  r2
4 o r  rn
atau
6
n
V(r )  
m 1
Qm
4 o r  rm
Jika masing-masing muatan titik dinyatakan sebagai unsur kecil sebuah
distribusi muatan ruang malar yang bermuatan v, maka
V( r ) 
 (r1 ) 1  (r2 ) 2
 (r ) n

 ...........   n
4 o r  r1 4 o r  r2
4 o r  rn
Distribusi muatan berbentuk muatan garis,
V(r )  
 L (r ' )dL'
4 o r  r '
Distribusi muatan berbentuk permukaan
V( r )  
s
 s (r ' )dS'
4 o r  r '
Muatan tersebar dalam bentuk volume
V( r ) 
 v (r ' )d '
 4
vol
o
r  r'
Sebagai gambaran dapat ditentukan potensial V pada sumbu z untuk muatan
garis serbasama L yang berbentuk cincin ,  = a pada bidang z = 0 seperti
pada gambar
z
(0,0,z)
r  r'  a 2  z2
=a
r
y
r’
’
x
dL = ad’;
r = z az ,
L
r’ = a a
r  r'  a 2  z2
7
dL’ = ad’
2
V
 4
0

 Lad '
o
a 2  z2

2
 La
4 o a 2  z 2
 d '
0
 La
2 o a 2  z 2
Contoh 3:
Tentukan potensial pada rA = 5 m terhadap rB = 15 dengan suatu muatan Q =
500 pC di titik asal, dan titik acuan nol di tak terhingga.
 Untuk muatan di titik asal:
VAB 
VAB
Q 1 1
  
4 o  rA rB 
500.10 12
1 1 

    0,6 Volt
4 (8,854.10 12 )  5 15 
 Acuan nol di tak terhingga dpt dipakai mencari V 5 dan V15
500.10 12
1
V15 
   0,30 V
12
4 (8,854.10 )  15 
500.10 12
1
V5 
 0,90 V;
12  
4 (8,854.10 )  5 
VAB = V5 – V15 = 0,6 Volt
Contoh 4:
Muatan sebesar (40/3) nC didistribusikan secara merata pada suatu cincin
berjari-jari 2 m. Tetapkan potensial pada suatu titik di poros cincin itu sejauh
5 m dari bidang cincin. Bandingkan hasilnya jika seluruh muatan berkumpul
di titik asal.
V(r )  
 L (r ' )dL'
4 o r  r '
z
(0,0,5
)
(40 / 3).109
L 
 1,06x10 09 C/m
2 (2)
r  r '  29
=2
0
5
r-r’= (22 + 52)1/2 = 29
2
dL’ = (2 m) d
’
x
8
L
y
dL’ = 2d’
2
V
(1,06x1009 )(2)d
0 (4x8,854x1012 )( 29)  22,3
Volt
9