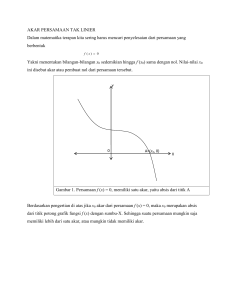
MATEMATIKA I (TEKNIK INFORMATIKA/SISTEM KOMPUTER) TIM PENYUSUN: NI LUH PUTU LABASARIYANI, S.Pd, M.Pd KETUT SEPDYANA KARTINI, S.Pd., M.Si NI LUH PUTU MERY MARLINDA, S.Pd, M.Pd NI WAYAN SUARDIATI PUTRI, S.Pd, M.Pd KADEK SURYATI, S.Pd, M.Pd DENPASAR AGUSTUS 2020 Metode Jacobi Metode Jacobi merupakan salah satu metode tak langsung, yang bermula dari suatu hampiran penyelesaian awal dan kemudian berusaha memperbaiki hampiran dalam tak berhingga namun langkah konvergen. Metode iterasi Jacobi ini digunakan untuk menyelesaikan persamaan linier yang proporsi koefisien nol nya besar. Metode ini ditemukan olek matematikawan yang berasal dari Jerman, Carl Gustav Jakob Jacobi. Penemuan ini diperkirakan pada tahun 1800-an. Iterasi dapat diartikan sebagai suatu proses atau metode yang digunakan secara berulang-ulang (pengulangan) dalam menyelesaikan suatu permasalahan matematika. Jika diubah dari persamaan linier, maka akan menjadi : Kemudian diketahui bahwa A = D + (L + U), dimana D merupakan matriks diagonal, L merupakan matriks segitiga bawah, dan U merupakan matriks segitiga atas. Lalu persamaan tersebut diubah menjadi; Jika ditulis dalam aturan iteratif, maka metode iterasi Jacobi dapat ditulis sebagai berikut : Dimana k merupakan banyaknya iterasi. Jika x (k) menyatakan hampiran ke –k penyelesaian SPL, maka x (0) adalah hampiran awal. Suatu matriks A berukuran n x n dikatakan dominan secara diagonal apabila : Contoh. Berikut adalah gambaran bagaimana menggunakan metode iterasi Jacobi dengan sebuah contoh. Misalkan ingin menyelesaikan SPL : Penyelesaian Nyatakan terlebih dahulu setiap variabel dalam ketiga variabel yang lain: 1. Nyatakan x1 dari persamaan (P1) dalam x2, x3, dan x4. 2. Nyatakan x2 dari persamaan (P2) dalam x1, x3, dan x4. 3. Nyatakan x3 dari persamaan (P3) dalam x1, x2, dan x4. 4. Nyatakan x4 dari persamaan (P4) dalam x1, x2, dan x3. Hasilnya adalah sistem persamaan linear, sbb. Nyatakan bahwa nilai x1, x2, x3, dan x4 yang berada di ruas kiri = (baca : sama dengan) sebagai x (baru). Sementara nilai x1, x2, x3, dan x4 yang berada di ruas kanan tanda = (baca : sama dengan) sebagai x (lama). Sehingga sistem persamaan tersebut dapat ditulis seperti : yang secara umum dapat diformulasikan sebagai persamaan matrik berikut ini : dimana Pada persamaan diatas, indeks k menunjukan jumlah perhitungan iterasi. Pada k = 1, dapat ditulis persamaan linier sebagai berikut : Jika diberikan nilai-nilai awal x (0) adalah x1 (0) = 0, x2 (0) = 0, x3 (0) = 0, dan x4 (0) = 0, atau dinyatakan sebagai hampiran awal x (0) = (0;0;0;0)T , maka hampiran pertama pada penyelesaian tersebut adalah : Maka diperoleh nilai-nilai x (3) = (0.9326; 2.0530; -1.0493; 1.1309)T . Lalu proses perhitungan diulangi lagi dengan k = 4. Begitulah seterusnya. Proses ini diulangi berkali-kali untuk nilai-nilai k berikutnya. Proses yang berulang ini disebut proses iterasi. Sampai dengan x (3) di atas, telah dilakukan tiga kali proses iterasi. Proses iterasi akan terus berlanjut sampai x (baru) mendekati solusi yang tepat, yaitu : x = (1; 2; -1; 1)T dengan kata lain, proses iterasi harus dihentikan bila x (baru) sudah mendekati solusi. Matriks Hessian Matriks Hessian adalah matriks yang setiap elemennya dibentuk dari turunan pasial kedua dari suatu fungsi. Misalkan ƒ(x) fungsi dengan n variabel yang memiliki turunan parsial kedua dan turunannya kontinu. Definisi Jika terdapat suatu matriks berukuran n × n, maka principal minor ke k di mana k ≤ n adalah suatu sub matriks dengan ukuran k × k yang diperoleh dengan menghapus (n — k) baris dan kolom yang bersesuaian dari matriks tersebut. Contoh Andaikan A adalah suatu matriks berukuran 3 × 3 sebagai berikut: 2 6 3 A = [1 5 2] 3 4 1 maka, principal minor ke-1 adalah [2], [5] dan [1]. Principal minor ke-2 adalah matriks (2 × 2) sebagai berikut: [2 6 ] 1 5 [2 3 ] 3 1 [5 2 ] 4 1 Principal minor ke-3 adalah matriks A itu sendiri. Determinan dari suatu principal minor disebut dengan determinan principal. Leading principal minor ke k dari suatu matriks (n × n) diperoleh dengan menghapus (n — k) baris terakhir dan kolom yang bersesuaian. Dari matriks A di atas, maka leading principal minor ke-1 adalah 2 (hapus dua baris dan dua kolom terakhir). Leading principal minor ke-2 adalah: [2 6 ] 1 5 Dengan demikian, leading principal minor ke-3 adalah matriks A itu sendiri. Determinan dari suatu leading principal minor adalah determinan leading principal. Banyaknya determinan leading principal dari suatu matriks (n × n) adalah n. Untuk menentukan apakah suatu matriks adalah definit positif, semidefinit positif, definit negatif, semidefinit negatif, atau indefinit dapat dilakukan suatu pengujian sederhana di mana hanya berlaku jika matriksnya simetris. Uji Matriks Definit Positif 1. Semua elemen diagonal positif. 2. Semua determinan leading principal positif. Uji Matriks Semidefinit Positif 1. Semua elemen diagonal non negatif. 2. Semua determinan leading principal non negatif. Suatu matriks dapat dikatakan definit negatif (semidefinit negatif), yaitu dengan melakukan uji negatif dari matriks untuk definit positif (semidefinit positif). Jika matriks tersebut memiliki sekurang-kurangnya dua elemen diagonal yang berlawanan tanda, maka matriks tersebut menjadi indefinit. & 2ƒ = 2x1, dan &x2 &2ƒ &x1x2 &2ƒ = &x2x1 = 2x2 — 4 Jadi matriks Hessiannya menjadi H=[ 6x1 2x2— 4 2x2 — 4 2x1 ] sehingga diperoleh H1 = [6x1], karena matriks H2 merupakan matriks H maka 6x1 2x2 — 4 H2 = H =2x [ — ] 4 2x1 2 Grafik ƒ(x) dalam ruang tiga dimensi diperlihatkan oleh Gambar 2.3. 2 (— √3, 2) 3 (0,4) 2 ( √3, 2) 3 (0,0) Gambar 2.3 Grafik ƒ(x1, x2) = x3 + x1x2 — 4x1x2 + 1 1 2