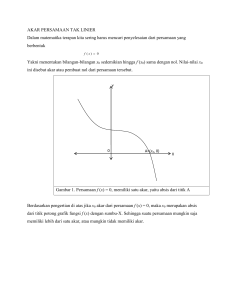
1. Pengertian Metode Newton-Rapshon merupakan salah satu metode terbuka untuk menentukan solusi akar dari persamaan non linier, dengan prinsip utama sebagai berikut: 1) Metode ini melakukan pendekatan terhadap kurva f(x) dengan garis singgung (gradien) pada suatu titik nilai awal. 2) Nilai taksiran selanjutnya adalah titik potong antara garis singgung (gradien) kurva dengan sumbu x 2. Grafik 3. Algoritma Metode Newton-Raphson 1. Definisikan fungsi f(x) dan f ’(x) 2. Tentukan toleransi error (e) dan iterasi maksimum (n) 3. Tentukan nilai pendekatan awal x0 4. Hitung f(x0) dan f ’(x0) 5. Untuk iterasi I = 1 s/d n atau |f(xi)|> e Hitung f(xi) dan f1(xi) Xi+1 = xi – 6. Akar persamaan adalah nilai xi yang terakhir diperoleh. 4. Pendekatan Ada dua pendekatan dalam menurunkan rumus metode newton rapshon, yaitu: a. Penurunan rumus metode newton rapshon secara geometri b. Penurunan rumus metode newton raphson dengan bantuan deret taylor a. Metode geometri y = f(x) Garis singgung kurva di Xi dengan gradien = f’ (Xi) Xi+1 Xi b. Metode deret taylor Kondisi iterasi berhenti bila: atau bila menggunakan galat relatif hampiran: Dengan dan diinginkan. adalah toleransi galat yang 5. Kelebihan & Kekurangan Kelebihan Metode newton raphson sangat cepat untuk menemukan akar (jika iterasinya konvergen) Kekurangan Metode newton rapshon sulit mencari akar jika f ’(x) terlalu dekat ke nol Tebakan awal tidak akan selalu mendekati nilai akar sejati 6 Contoh Tentukan akar dari persamaan 4x3 – 15x2 + 17x – 6 = 0 menggunakan Metode Newton-Raphson.Dengan X0=3 Dan E=0.00001 Penyelesaian f(x) = 4x3 – 15x2 + 17x – 6 f’(x) = 12x2 – 30x + 17 iterasi 0: ambil titik awal x0 = 3 f(3) = 4(3)3 – 15(3)2 + 17(3) – 6 = 18 f’(3) = 12(3)2 – 30(3) + 17 = 35 x1 = 3= 2.48571 iterasi 1 : f(2.48571) = 4(2.48571)3 – 15(2.48571)2 + 17(2.48571) – 6 = 5.01019 f’(2.48571) = 12(2.48571)2 – 30(2.48571) + 17 = 16.57388 x2 = 2.48571 – = 2.18342 iterasi 2 : f(2.18342) = 4(2.18342)3 – 15(2.18342)2 + 17(2.18342) – 6 = 1.24457 f’(2.18342) = 12(2.18342)2 – 30(2.18342) + 17 = 8.70527 x3 = 2.18342 – = 2.04045 iterasi 3 : f(2.04045) = 4(2.04045)3 – 15(2.04045)2 + 17(2.04045) – 6 = 0.21726 f’(2.04045) = 12(2.04045)2 – 30(2.04045) + 17 = 5.74778 x4 = 2.04045 – = 2.00265 iterasi 4 : f(3) = 4(2.00265)3 – 15(2.00265)2 + 17(2.00265) – 6 = 0.01334 f’(2.00265) = 12(2.00265)2 – 30(2.00265) + 17 = 5.04787 x5 = 2.00265 – = 2.00001 iterasi 5: f(2.00001) = 4(2.00001)3 – 15(2.00001)2 + 17(2.00001) – 6 = 0.00006 f’(2.00001) = 12(2.00001)2 – 30(2.00001) + 17 = 5.00023 x6 = 2.00001 – = 2.00000 iterasi 6 : f(2) = 4(2)3 – 15(2)2 + 17(2) – 6 = 0 Tabel i 0 xi 3 f(xi) 18 f’(xi) 35 1 2.48571 5.01019 16.57388 2 2.18342 1.24457 8.70527 3 2.04045 0.21726 5.74778 4 2.00265 0.01334 5.04787 5 2.00001 0.00006 5.00023 6 2.00000 0.00000 5.00000 Jika disajikan dalam tabel maka karena pada iterasi f(X6)=0 maka akar persamaannya adalah =2.00000 TERIMAKASIH