penyelesaian sistem persamaan tak linier # pengantar # # metode
advertisement
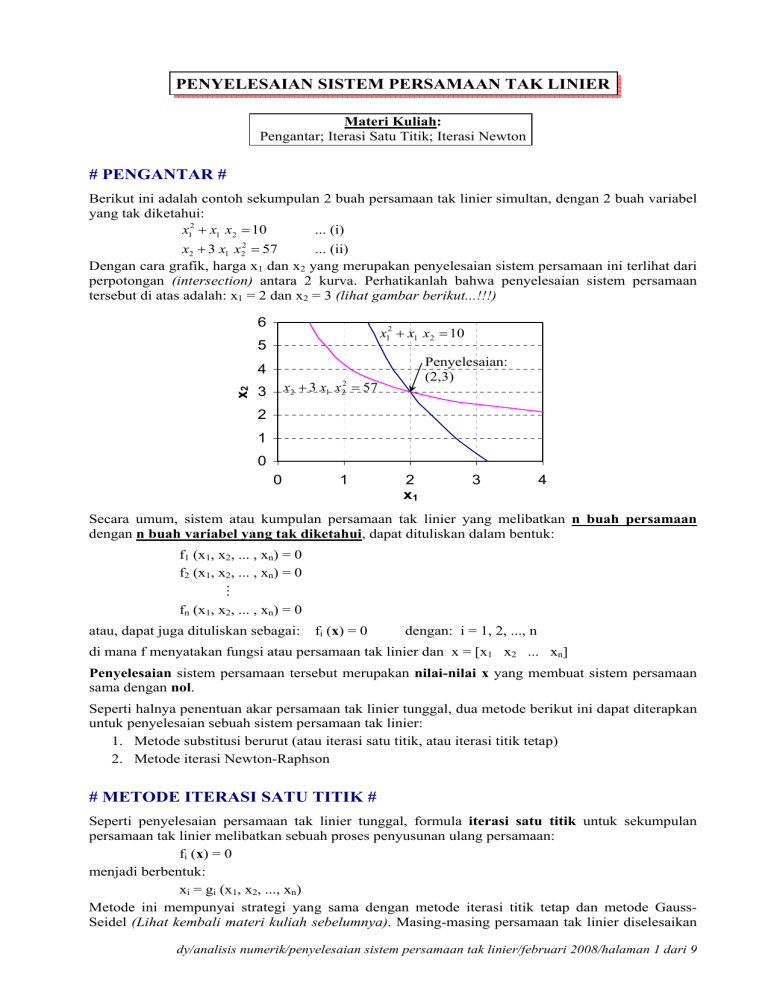
PENYELESAIAN SISTEM PERSAMAAN TAK LINIER Materi Kuliah: Pengantar; Iterasi Satu Titik; Iterasi Newton # PENGANTAR # Berikut ini adalah contoh sekumpulan 2 buah persamaan tak linier simultan, dengan 2 buah variabel yang tak diketahui: x12 + x1 x2 = 10 ... (i) 2 x2 + 3 x1 x2 = 57 ... (ii) Dengan cara grafik, harga x1 dan x2 yang merupakan penyelesaian sistem persamaan ini terlihat dari perpotongan (intersection) antara 2 kurva. Perhatikanlah bahwa penyelesaian sistem persamaan tersebut di atas adalah: x1 = 2 dan x2 = 3 (lihat gambar berikut...!!!) 6 x12 + x1 x2 = 10 5 Penyelesaian: (2,3) x2 4 x2 + 3 x1 x22 = 57 3 2 1 0 0 1 2 x1 3 4 Secara umum, sistem atau kumpulan persamaan tak linier yang melibatkan n buah persamaan dengan n buah variabel yang tak diketahui, dapat dituliskan dalam bentuk: f1 (x1, x2, ... , xn) = 0 f2 (x1, x2, ... , xn) = 0 # fn (x1, x2, ... , xn) = 0 atau, dapat juga dituliskan sebagai: fi (x) = 0 dengan: i = 1, 2, ..., n di mana f menyatakan fungsi atau persamaan tak linier dan x = [x1 x2 ... xn] Penyelesaian sistem persamaan tersebut merupakan nilai-nilai x yang membuat sistem persamaan sama dengan nol. Seperti halnya penentuan akar persamaan tak linier tunggal, dua metode berikut ini dapat diterapkan untuk penyelesaian sebuah sistem persamaan tak linier: 1. Metode substitusi berurut (atau iterasi satu titik, atau iterasi titik tetap) 2. Metode iterasi Newton-Raphson # METODE ITERASI SATU TITIK # Seperti penyelesaian persamaan tak linier tunggal, formula iterasi satu titik untuk sekumpulan persamaan tak linier melibatkan sebuah proses penyusunan ulang persamaan: fi (x) = 0 menjadi berbentuk: xi = gi (x1, x2, ..., xn) Metode ini mempunyai strategi yang sama dengan metode iterasi titik tetap dan metode GaussSeidel (Lihat kembali materi kuliah sebelumnya). Masing-masing persamaan tak linier diselesaikan dy/analisis numerik/penyelesaian sistem persamaan tak linier/februari 2008/halaman 1 dari 9 untuk memperoleh sebuah nilai x yang tak diketahui. Sistem persamaan ini selanjutnya diproses secara iteratif untuk menghitung nilai-nilai x yang baru, yang diharapkan akan konvergen kepada penyelesaian yang sesungguhnya. Contoh: Gunakan metode substitusi berurut untuk menentukan akar-akar persamaan: x12 + x1 x2 = 10 ...(a) 2 x2 + 3 x1 x2 = 57 ...(b) Gunakan nilai tebakan awal: x1 = 1,5 dan x2 = 3,5 Bandingkan hasilnya dengan nilai x1 dan x2 yang sesungguhnya. Penyelesaian: Masing-masing persamaan (a) dan (b) dapat disusun ulang (rearranging) untuk memperoleh harga x1 dan x2 sebagai berikut: 10 − x12 x1 = dan x2 = 57 − 3 x1 x22 x2 Iterasi pertama: Dengan menggunakan nilai awal x1 = 1,5 dan x2 = 3,5, maka x1 (baru) dapat dihitung dengan cara: 10 − (1,5) 2 x1 = = 2,21429 3,5 Nilai x1 (baru) ini dan nilai x2 (lama) selanjutnya dapat dihitung untuk menghitung nilai x2 (baru): x2 = 57 − 3 (2,21429) (3,5) 2 = −24,37516 Iterasi kedua: Dengan cara yang sama, diperoleh: 10 − (2,21429) 2 = −0,20910 x1 = − 24,37516 x2 = 57 − 3 (−0,20910) (−24,37516) 2 = 429,709 Perhatikanlah bahwa pendekatan ini menghasilkan penyelesaian yang divergen...!! Oleh karena itu, persamaan (a) dan (b) disusun ulang kembali dengan cara yang berbeda, misalnya: Dari persamaan (a) : x1 = 10 − x1 x2 dan, dari persamaan (b) : x2 = 57 − x2 3 x1 Iterasi pertama: x1 = 10 − (1,5) (3,5) = 2,17945 x2 = 57 − 3,5 = 2,86051 3 (2,17945) Iterasi kedua: x1 = 10 − (2,17945) (2,86051) = 1,94053 x2 = 57 − 2,86051 = 3,04955 3 (1,94053) Perhatikanlah bahwa pendekatan ini menghasilkan penyelesaian yang konvergen ke arah nilai-nilai yang sesungguhnya (x1 = 2 dan x2 = 3) Hasil-hasil perhitungan selengkapnya disajikan dalam tabel berikut ini: dy/analisis numerik/penyelesaian sistem persamaan tak linier/februari 2008/halaman 2 dari 9 # METODE ITERASI NEWTON-RAPHSON # Ingat kembali metode Newton-Raphson untuk menentukan akar persamaan tak linier tunggal (pada materi sebelumnya). Untuk persamaan tak linier tunggal, cara lain untuk menyusun formulanya adalah dengan menurunkannya dari ekspansi deret Taylor order-pertama: f ( xi +1 ) = f ( xi ) + ( xi +1 − xi ) f ' ( xi ) di mana xi adalah nilai tebakan awal x dan xi+1 adalah nilai x yang merupakan perpotongan antara slope f’(x) dengan sumbu x. Karena pada perpotongan ini, f(xi+1) bernilai nol, maka persamaan di atas dapat disusun ulang menjadi: f ( xi ) xi +1 = xi − f ' ( xi ) yang merupakan formula Newton-Raphson untuk persamaan tunggal. Pendekatan di atas selanjutnya dapat diterapkan untuk kumpulan atau sistem persamaan tak linier, yang terdiri atas n buah persamaan, dengan n buah variabel bebas yang tak diketahui. Sebagai contoh, ekspansi deret Taylor order-pertama untuk 2 buah variabel dapat dituliskan sbb.: f1,i +1 = f1,i + ( x1,i +1 − x1,i ) f 2,i +1 = f 2,i + ( x1,i +1 − x1,i ) ∂ f1,i ∂ x1 ∂ f 2 ,i ∂ x1 + ( x2,i +1 − x2,i ) ∂ f1,i + ( x2,i +1 − x2,i ) ∂ x2 ∂ f 2 ,i ∂ x2 Karena f1,i+1 dan f2,i+1 bernilai nol, maka kedua persamaan di atas dapat disusun ulang menjadi: ∂ f1,i ∂ x1 ∂ f 2,i ∂ x1 x1,i +1 + x1,i +1 + ∂ f1,i ∂ x2 ∂ f 2,i ∂ x2 x2,i +1 = − f1,i + x1,i x2,i +1 = − f 2,i + x1,i ∂ f1,i + x2,i ∂ x1 ∂ f 2,i ∂ x1 + x2,i ∂ f1,i ∂ x2 ∂ f 2,i ∂ x2 Suku-suku yang mengandung subscript i telah diketahui nilainya; sedangkan suku-suku yang mengandung subscript i+1 yang akan dihitung. Dengan cara lain, kedua persamaan di atas dapat disusun dalam bentuk matriks (yakni perkalian sebuah matriks bujur sangkar dengan sebuah vektor yang menghasilkan sebuah vektor) menjadi: ⎡ ∂ f1,i ⎢∂x 1 ⎢ ⎢ ∂ f 2,i ⎢∂x 1 ⎣ ∂ f1,i ⎤ ⎡ x ⎤ ⎡ ⎢ 1,i +1 ⎥ ⎢ − f1,i + x1,i ∂ x2 ⎥⎥ ⎢ ⎥ = ⎢ ∂ f 2,i ⎥ ⎢ ⎥ ⎢ x ⎢ ⎥ ⎢− f 2,i + x1,i ⎥ 2 , i + 1 ∂ x2 ⎦ ⎣ ⎦ ⎣ A x = ∂ f1,i ∂ x1 ∂ f 2,i ∂ x1 b + x2,i + x2 ,i ∂ f1,i ⎤ ∂ x2 ⎥⎥ ∂ f 2,i ⎥ ∂ x2 ⎥⎦ dy/analisis numerik/penyelesaian sistem persamaan tak linier/februari 2008/halaman 3 dari 9 Selanjutnya, besarnya vektor x dapat ditentukan. Matriks A dalam sistem persamaan ini sering disebut sebagai matriks Jacobian. Nilai-nilai x1,i+1 dan x2,i+1 juga dapat ditentukan melalui manipulasi aljabar (misalnya dengan cara Cramer), menghasilkan: x1,i +1 ∂ f 2,i ∂ f1,i − f 2,i ∂ x2 ∂ x2 = x1,i − ∂ f1,i ∂ f 2,i ∂ f1,i ∂ f 2,i − ∂ x1 ∂ x2 ∂ x2 ∂ x1 x2,i +1 ∂ f1,i ∂ f 2,i − f1,i ∂ x1 ∂ x1 = x 2 ,i − ∂ f1,i ∂ f 2,i ∂ f1,i ∂ f 2,i − ∂ x1 ∂ x2 ∂ x2 ∂ x1 f1,i f 2,i Contoh: Gunakan metode Newton-Raphson multiple-equations untuk menentukan akar-akar persamaan: x12 + x1 x2 = 10 ...(a) 2 x2 + 3 x1 x2 = 57 ...(b) Gunakan nilai tebakan awal: x1 = 1,5 dan x2 = 3,5 Bandingkan hasilnya dengan nilai x1 dan x2 yang sesungguhnya. Penyelesaian: Persamaan (a) dan (b) dapat dituliskan kembali dalam bentuk: f1 = x12 + x1 x2 − 10 = 0 f 2 = x2 + 3 x1 x22 − 57 = 0 Fungsi turunan parsial pertama untuk f1 dan f2: ∂ f2 ∂ f1 = 3 x22 = 2 x1 + x2 ∂ x1 ∂ x1 ∂ f1 ∂ f2 = x1 = 1 + 6 x1 x2 ∂ x2 ∂ x2 Iterasi pertama: Untuk nilai tebakan awal: x1,0 = 1,5 dan x2,0 = 3,5, nilai-nilai turunan parsialnya adalah: ∂ f1,0 = 2 x1,0 + x2,0 = 2 (1,5) + 3,5 = 6,5 ∂ x1 ∂ f1, 0 = x1,0 = 1,5 ∂ x2 ∂ f 2, 0 = 3 x22, 0 = 3 (3,5) 2 = 36,75 ∂ x1 ∂ f 2,0 = 1 + 6 x1, 0 x2, 0 = 1 + 6 (1,5) (3,5) = 32,5 ∂ x2 Nilai determinan matriks Jacobian: Δ = (6,5) (32,5) – (1,5) (36,75) = 156,125 Nilai fungsi f1 dan f2: f1, 0 = x12,0 + x1,0 x2,0 − 10 = (1,5) 2 + (1,5) (3,5) − 10 = −2,5 f 2, 0 = x2, 0 + 3 x1,0 x22,0 − 57 = 3,5 + 3 (1,5) (3,5) 2 − 57 = 1,625 Dengan demikian, x1 dan x2 (baru) dapat dihitung sebagai berikut: dy/analisis numerik/penyelesaian sistem persamaan tak linier/februari 2008/halaman 4 dari 9 − 2,5 (32,5) − 1,625 (1,5) = 2,03603 156,125 1,625 (6,5) − (−2,5) (36,75) x2 = 3,5 − = 2,84388 156,125 x1 = 1,5 − Komentar: Langkah perhitungan ini dapat diulangi hingga diperoleh tingkat akurasi yang diinginkan. Perhatikan bahwa hasil perhitungan bersifat konvergen menuju nilai-nilai x1 dan x2 yang sesungguhnya. Hasil-hasil perhitungan selengkapnya disajikan dalam tabel berikut ini: Contoh: Tentukan akar persamaan: (i) y = 1− ex (ii) x 2 + y 2 = 4 (Persamaan lingkaran) f1 ( x, y ) = e x + y − 1 = 0 f 2 ( x, y ) = x 2 + y 2 − 4 = 0 atau: atau: secara iteratif dengan menggunakan metode Newton. Penyelesaian: Secara grafik, terlihat bahwa sistem persamaan tak linier ini mempunyai 2 buah akar (yang terlihat dari perpotongan antara grafik f1 dan f2). 3 f2 y Akar-akar persamaan 2 1 x 0 -3 -2 -1 0 1 2 3 -1 -2 f1 -3 Dengan cara yang sama dengan contoh penyelesaian soal sebelumnya, akan dicoba 2 buah nilai tebakan awal x dan y yang berbeda. Hasil-hasil perhitungan selengkapnya, dengan mengambil nilai awal: x = 1; y = -2 dy/analisis numerik/penyelesaian sistem persamaan tak linier/februari 2008/halaman 5 dari 9 Hasil-hasil perhitungan selengkapnya, dengan mengambil nilai awal: x = -1; y = 1 Komentar: Perhatikanlah bahwa dengan mengambil nilai tebakan awal x dan y yang berbeda, maka hasil perhitungan masing-masing bersifat konvergen dan mengarah kepada posisi akar persamaan yang berbeda pula. Generalization Secara umum, untuk sejumlah n buah persamaan tak linier, dengan n buah variabel bebas yang tak diketahui, berlaku hubungan: ∂ f k ,i ∂ x1 x1,i +1 + ∂ f k ,i ∂ x2 x2,i +1 + ... + ∂ f k ,i ∂ xn xn,i +1 = − f k ,i + x1,i ∂ f k ,i ∂ x1 + x2 ,i ∂ f k ,i ∂ x2 + ... + xn,i ∂ f k ,i ∂ xn dengan k menyatakan persamaan atau variabel yang tak diketahui; i menyatakan nilai (atau iterasi) sekarang; dan i+1 menyatakan nilai (atau iterasi) berikutnya. Jika persamaan umum di atas disusun untuk k = 1, 2, ..., n, terlihat bahwa sistem persamaan yang terbentuk merupakan sekumpulan persamaan linier simultan, yang dapat diselesaikan secara numerik melalui beberapa metode. Dalam bentuk matriks, sistem persamaan di atas dapat dituliskan sebagai: [Z] [xi+1] = - [f] + [Z] [xi] dengan turunan parsial yang dituliskan sebagai matriks Jacobian dinyatakan sebagai: dy/analisis numerik/penyelesaian sistem persamaan tak linier/februari 2008/halaman 6 dari 9 ⎡∂ f ∂ f1,i ∂ f1,i ⎤ ⎢ 1,i ⎥ " ∂ x2 ∂ xn ⎥ ⎢ ∂ x1 ⎢ ∂ f 2,i ∂ f 2,i ∂ f 2,i ⎥ " ⎢ ⎥ [ Z ] = ⎢ ∂ x1 ∂ x2 ∂ xn ⎥ # ⎥ ⎢ # ⎢ ∂ f n ,i ∂ f n ,i ∂ f n ,i ⎥ " ⎢ ⎥ ∂ x2 ∂ xn ⎥ ⎢⎣ ∂ x1 ⎦ Nilai-nilai awal dan akhir dituliskan dalam bentuk vektor: [xi]T = [x1,i x2,i ... xn,i] dan [xi+1]T = [x1,i+1 x2,i+1 ... xn,i+1] Nilai fungsi pada i dapat dinyatakan dalam bentuk: [f]T = [f1,i f2,i ... fn,i] Permasalahan yang dijumpai dalam penyelesaian sistem persamaan tak linier dengan metode Newton-Raphson sama dengan permasalahan penyelesaian persamaan tunggal, yakni: 1) Evaluasi fungsi turunan pertama kadang-kadang sulit dilakukan; hal ini bisa diatasi dengan penerapan finite-difference approximation, dan 2) Pemilihan nilai tebakan awal yang tepat diperlukan untuk menjamin terjadinya konvergensi penyelesaian. Finite-difference approximation: f ( x + Δx j ) − f i ( x j ) ∂ fi ≈ i j ∂ xj Δx j (forward difference) f ( x + Δx j ) − f i ( x j − Δx j ) ∂ fi ≈ i j ∂ xj 2 Δx j (central or center difference) f ( x ) − f i ( x j − Δx j ) ∂ fi ≈ i j ∂ xj Δx j (backward difference) Contoh Aplikasi: Berikut ini adalah skema reaksi kompleks dari sebuah sistem reaksi fase cair: r1 A 2B r2 A C r3 r4 B D+C dengan: k1 = 1,0 detik-1 [=] gmol/L.detik r1 = k1 CA r2 = k2 CA3/2 [=] gmol/L.detik k2 = 0,2 liter1/2/gmol1/2.detik 2 [=] gmol/L.detik r3 = k3 CC k3 = 0,05 L/gmol.detik 2 [=] gmol/L.detik r4 = k4 CB k4 = 0,4 L/gmol.detik Sebuah continuously stirred tank reactor (CSTR) bervolume (VR) 100 liter digunakan untuk sistem reaksi ini. Reaktan dengan konsentrasi A (CA) 1,0 mol/L diumpankan dengan laju alir volumetrik (Q) 50 liter/detik. CSTR dirancang beroperasi pada keadaan steady dan sistem reaksi diasumsikan beroperasi pada kondisi isotermal. dy/analisis numerik/penyelesaian sistem persamaan tak linier/februari 2008/halaman 7 dari 9 Neraca massa (mol) untuk masing-masing komponen reaksi dapat dituliskan sebagai berikut: Out CA Q CB Q CC Q CD Q Komponen A: Komponen B: Komponen C: Komponen D: = = = = = In CA0 Q 0 0 0 + Generation + VR (r3) + VR (2 r1) + VR (r2 + r4) + VR (r4) - Consumption - VR (r1 + r2) - VR (r4) - VR (r3) -0 Dengan mensubstitusikan persamaan ri ke dalam neraca mol di atas, maka diperoleh 4 buah persamaan tak linier simultan berikut: 3 ⎞ V ⎛ f1 = −C A + C A0 + R ⎜⎜ − k1 C A − k2 C A 2 + k3 CC2 ⎟⎟ = 0 Q⎝ ⎠ f 2 = −CB + VR ⎛ 2 ⎜ 2 k1 C A − k4 CB ⎞⎟ = 0 ⎠ Q⎝ f 3 = −CC + 3 ⎞ VR ⎛ ⎜⎜ k2 C A 2 − k3 CC2 + k 4 CB2 ⎟⎟ = 0 Q⎝ ⎠ VR ⎛ 2 ⎜ k4 CB ⎞⎟ = 0 ⎠ Q⎝ Tentukan besarnya CA, CB, CC, dan CD dengan menngunakan metode Newton. Gunakan nilai-nilai awal: CA,0 = CB,0 = CC,0 = CD,0 = 0,3 f 4 = −C D + Penyelesaian: Untuk menerapkan metode Newton, turunan parsial dari masing-masing persamaan terhadap masing-masing variabel perlu ditentukan, untuk menghasilkan matriks Jacobian. Berikut merupakan non-zero partial derivatives untuk sistem ini: ∂ f 3 VR ⎛ 1 ⎞ ∂ f1 V ⎛ = ⎜ 2 k 4 CB ⎞⎟ = −1 − R ⎜⎜ k1 + 1,5 k2 C A 2 ⎟⎟ ⎠ ∂ C Q⎝ ∂ CA Q⎝ B ⎠ ∂ f3 V ∂ f1 VR ⎛ = −1 − R ⎛⎜ 2 k3 CC ⎞⎟ = ⎜ 2 k3 CC ⎞⎟ ⎠ Q⎝ ∂ CC ⎠ ∂ CC Q ⎝ ∂ f 4 VR ⎛ ∂ f 2 VR = ⎜ 2 k 4 CB ⎞⎟ = 2 k1 ⎝ ⎠ C Q ∂ B ∂ CA Q ∂ f4 ∂ f2 V = −1 = −1 − R ⎛⎜ 2 k 4 C B ⎞⎟ ∂ C D ⎠ ∂C Q⎝ ( ) B 1 ⎞ ∂ f 3 VR ⎛ = ⎜⎜1,5 k 2 C A 2 ⎟⎟ ∂ CA Q ⎝ ⎠ Hasil perhitungan secara iteratif (silakan Anda coba menghitung sendiri...!!!): i CA CB CC CD 0 0,3 0,3 0,3 0,3 1 0,3150712 0,9001920 0,4148786 0,3600919 2 0,3183329 0,7874451 0,5308877 0,4858863 3 0,3188652 0,7838874 0,5349776 0,4915732 4 0,3188658 0,7838840 0,5349814 0,4916789 Berdasarkan hasil perhitungan di atas, terlihat bahwa 4 langkah iterasi telah menunjukkan hasil (atau penyelesaian) yang konvergen. # LATIHAN SOAL # 1. Tentukan penyelesaian sistem persamaan tak linier simultan berikut ini: y = -x2 + x + 0,5 y + 5 x y = x2 Gunakan metode Newton-Raphson dan gunakan nilai tebakan awal x = y = 1,2 dy/analisis numerik/penyelesaian sistem persamaan tak linier/februari 2008/halaman 8 dari 9 2. Tentukan penyelesaian sistem persamaan tak linier simultan berikut ini: x2 = 5 – y2 y + 1 = x2 menggunakan: (a) metode grafik (b) metode substitusi berurut; dengan nilai tebakan awal x = y = 1,5 (c) metode Newton-Raphson; dengan nilai tebakan awal x = y = 1,5 3. Lakukan 3 langkah iterasi dengan metode Newton untuk menyelesaikan sekumpulan persamaan tak linier berikut: f ( x) = 2 x12 + 3 x22 − 50 = 0 f ( x) = 2 x12 − x2 − 9 = 0 Gunakan nilai awal x = [1 1] 4. Selesaikan sistem persamaan tak linier berikut: f1 = 5 ( x2 − x12 ) 4 = 0 f 2 = (1 − x1 ) 2 = 0 Gunakan x1,0 = x2,0 = 0 dengan metode Newton. Gunakan nilai awal x yang lain, jika perlu. 5. Selesaikan sistem persamaan tak linier berikut: x13 − e x 2 + sinh x3 = 3,62882 x12 x3 + ( x22 − x3 ) 2 = 4,0 x1 x2 x3 − x3 + x1 x2 = 5,0 Gunakan x1,0 = x2,0 = x3,0 = 0 dengan metode Newton. Gunakan nilai awal x yang lain, jika penyelesaian yang diperoleh tidak konvergen. 6. Tinjaulah sistem reaksi berkesetimbangan berikut ini: CH4 (g) + H2O (g) CO (g) + 3 H2 (g) ... (1) CO (g) + H2O (g) CO2 (g) + H2 (g) ... (2) Pada 2000 K, konstanta kesetimbangan untuk sistem reaksi ini masing-masing adalah sebesar 1,930 x 10-4 dan 5,528. Gas mula-mula mengandung 20%-mol CH4 (g) dan 80% H2O (g), yang berada pada kondisi 2000 K dan 1 atm. Konstanta kesetimbangan untuk kedua reaksi dinyatakan sebagai: y y yCO y H3 2 dan K1 = P2 K 2 = CO2 H 2 yCH 4 y H 2 O yCO yH 2 O Jika 10 mol gas dipilih sebagai basis perhitungan; ε1 menyatakan tingkat reaksi untuk reaksi (1) dan ε2 menyatakan tingkat reaksi untuk reaksi (2), maka fraksi mol komponen-komponen reaksi pada kesetimbangan dapat dinyatakan sebagai: 3ε + ε 8 − ε1 − ε 2 ε −ε y CO = 1 2 yH2 = 1 2 y H 2O = 10 + 2 ε1 10 + 2 ε1 10 + 2 ε1 2 − ε1 ε2 y CO2 = y CH 4 = 10 + 2 ε 1 10 + 2 ε1 Dengan mensubstitusikan 5 persamaan fraksi mol di atas ke dalam 2 persamaan konstanta kesetimbangan reaksi, diperoleh: (ε1 − ε 2 ) (3 ε1 + ε 2 )3 = 1,930 x 10− 4 2 (2 − ε1 ) (8 − ε1 − ε 2 ) (10 + 2 ε1 ) ε 2 (3 ε1 + ε 2 ) = 5,528 (ε1 − ε 2 ) (8 − ε1 − ε 2 ) Pertanyaan: Tentukan komposisi gas pada kesetimbangan untuk sistem reaksi ini! ☺☺☺ Selamat Belajar!!! ☺☺☺ dy/analisis numerik/penyelesaian sistem persamaan tak linier/februari 2008/halaman 9 dari 9











