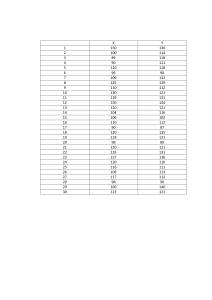
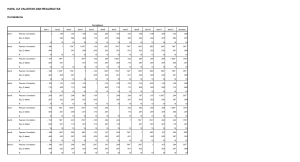
Materi 6: ANALISIS KORELASI Korelasi Bivariate (Dua Variabel) Ada tidaknya hubungan antara antara dua variabel dapat dilihat jika data dati variabel yang bersangkutan dibuat scatterplot (diagram pencar). Scatterplot merupakan langkah dasar untUk mengetahui ada tidaknya hubungan tadi. Sedangkan ukuran yang biasa digunakan untuk mengukur kekuatan hubungan (asosiasi) adalah Koefisien Kore/as; Pearson yang diberi notasi r sebagai : Dimana N adalah banyaknya kasus, Sx dan Sy adalah standar deviasi dari variabel X dan Y. Harga koefisien r berkisar antara 0 sampai dengan 1 atau -1. Harga absolut dari r menunjukkan kekuatan hubungan linier antar variabel-variabel yang bersangkutan. Harga r yang positif menunjukkan hubungan bahwa kenaikan harga dari suatu variabel akan diikuti dengan menaiknya harga-harga variabel yang lainnya. Demikian pula sebaliknya jika harga r negatif menunjukkan bahwa kenaikkan harga-harga suatu variabel akan diikuti dengan menurunnya harga-harga variabel yang lainnya. Jika r berharga 0, hal ini menunjukkan tidak adanya hubungan linier. Jika r berharga 1 dapat terjadi jika titik hasil observasi tepat jatuh pada garis lurus. Kemiringan garis menunjukkan apakah hubungannya berbentuk positif atau negatif. Mengadakan uji korelasi perlu dibarengi dengan pembuatan scatterplot, karena beberapa koefisien korelasi dapat dihasilkan dari berbagai bentuk hubungan yang berbeda. Dua variabel mempunyai koefisien korelasi yang hampir sarna meskipun hubungannya mungkin berbeda. Yang satu mempunyai hubungan yang linier dan yang lainnya mungkin hubungannya nonlinier. Koefisien korelasi yang dihasilkan merupakan langkah pertama untuk menjelaskan kekuatan hubungan linier antara dua variabel. Selanjutnya dapat diadakan uji hipotesis mengenai koefisien populasi yang tidak diketahui yaitu menguji p (rho) sama dengan nol. Korelasi Product Moment Pearson hanya cocok untuk data yang sedikitnya terdapat sebuah pengukuran dalam tingkat interval. Jika datanya dalam pengukuran ordinal atau interval dapat digunakan Koefisien Korelasi Rank Spearman. Koefisien korelasi yang disediakan adalah Koefisien Korelasi Kendall's taub. Korelasi Parsial Pada saat kita menguji hubungan antara dua variabel, kita juga harus mempertimbangkan pengaruh dari variabel-variabel lain dalam hubungan tersebut. Koefisien yang seperti ini disebut Koefisien Korelasi Parsial. Koefisien korelasi parsial adalah sebuah teknik yang berhubungan sangat erat dengan regresi linier berganda, yang memberikan ukuran hubungan (asosiasi) linier tunggal antara dua variabel yang disesuaikan dengan pengaruh liniear dari satu atau beberapa vanabel lainnya. Deskripsi lain dari korelasi parsial adalah, misalnya kita mempunyai 3 buah variabel yaitu v1, v2, dan v3 maka r12.3 adalah koefisien korelasi parsial antara v1 dan v2 pada satu kelompok dimana v3 dianggap konstan (sebagai variabel kontrol). Banyaknya variabel kontrol menentukan orde dari koefisien korelasi parsial. Jika terdapat sebuah variabel kontrol seperti contoh diatas, maka koefisien korelasi persialnya adalah parsial orde pertama. Jika terdapat dua variabel kontrol maka disebut parsial orde kedua dan seterusnya. Koefisien korelasi biasa (bivariabel) sering disebut korelasi zero order karena tidak mempunyai variabel kontrol. Uji signifikansi diperlukan untuk menguji hipotesis nol bahwa koefisien korela.si parsial populasi adalah O. Nilai statistik uji korelasi tersebut adalah : Dimana θ adalah orde koefisien, dan r adalah koefisien korelasi parsial. Derajat kebebasan dan t adalah N - θ - 2, dimana N adalah banyaknya kasus. Data : No. Y Xl X2 1. 5.92 4.90 4.78 2. 4.30 5.90 3.84 3. 3.30 5.60 3.13 4. 6.23 4.90 3.44 5. 10.97 5.60 6.84 6. 9.14 8.50 9.47 7. 5.77 7.70 6.51 8. 6.45 7.10 5.92 9. 7.60 6.10 6.08 10. 11.47 5.80 8.09 11. 13.46 7.10 10.01 12. 10.24 7.00 10.81 13. 5.99 9.70 Dimana : Y = Permintaan barang Xl = Harga barang X2 = Pendapatan konsumen. 8.00 Untuk menganalisis Korelasi antar variabel, awali dengan klik menu Analyze, pilih, Correlate, pilih Bivariate. Masukkan variabel Y, Xl, dan X2 ke dalam kotak Variables, kemudian tandai kotak Pearson, dan akhin dengan klik OK. Output Analisis Korelasi TUGAS : a. Bandingkan output analisis diatas dengan latihan yang dikerjakan! b. Interpretasikan masing-masing uji statistik (uji R2, uji F dan uji t) pada lembar jawaban yang telah disediakan! CORRELATIONS /VARIABLES=Y X1 X2 /PRINT=TWOTAIL NOSIG /MISSING=PAIRWISE. Correlations Notes Output Created 14-APR-2020 10:34:35 Comments Input Active Dataset DataSet0 Filter <none> Weight <none> Split File <none> N of Rows in Working 13 Data File Missing Value Handling Definition of Missing User-defined missing values are treated as missing. Cases Used Statistics for each pair of variables are based on all the cases with valid data for that pair. Syntax CORRELATIONS /VARIABLES=Y X1 X2 /PRINT=TWOTAIL NOSIG /MISSING=PAIRWISE. Resources Processor Time 00:00:00,00 Elapsed Time 00:00:00,18 [DataSet0] Correlations Permintaan Pendapatan Barang Permintaan Barang Harga Barang Pearson ,090 ,787** ,771 ,001 13 13 13 ,090 1 ,595* 1 Correlation Sig. (2-tailed) N Harga Barang Pearson Correlation Sig. (2-tailed) ,771 N Pendapatan Konsumen Pearson Correlation Sig. (2-tailed) Konsumen ,032 13 13 13 ,787** ,595* 1 ,001 ,032 13 13 N **. Correlation is significant at the 0.01 level (2-tailed). INTERPRETASI HASIL : Hubungan antara harga barang dengan permintaan barang Nilai signifikansi 0,771 > 0,05 maka harga barang tidak berkorelasi terhadap permintaan barang Nilai Pearson correlation = 0,090 maka harga barang tidak terdapat korelasi terhadap permintaan barang Hubungan antara pendapatan konsumen dengan permintaan barang Nilai signifikansi 0,001 < 0,05 maka pendapatan konsumen berkorelasi terhadap permintaan barang Nilai Pearson Correlation = 0,787 maka pendapatan kosumen memiliki korelasi kuat terhadap permintaan barang Hubungan harga barang dengan pendapatan konsumen 13 Nilai signifikansi 0,032 < 0,05 maka pendapatan konsumen berkorelasi terhadap harga barang Nilai Pearson Correlation = 0,595 maka pendapatan konsumen memiliki korelasi sedang terhadap harga barang