354481152-Distribusi-Normal

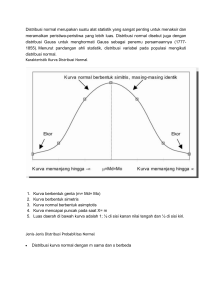
Distribusi normal merupakan suatu alat statistik yang sangat penting untuk menaksir dan
meramalkan peristiwa-peristiwa yang lebih luas. Distribusi normal disebut juga dengan
distribusi Gauss untuk menghormati Gauss sebagai penemu persamaannya (17771855). Menurut pandangan ahli statistik, distribusi variabel pada populasi mengikuti
distribusi normal.
Karakteristik Kurva Distribusi Normal
1.
2.
3.
4.
5.
Kurva berbentuk genta (m= Md= Mo)
Kurva berbentuk simetris
Kurva normal berbentuk asimptotis
Kurva mencapai puncak pada saat X= m
Luas daerah di bawah kurva adalah 1; ½ di sisi kanan nilai tengah dan ½ di sisi kiri.
Jenis-Jenis Distribusi Probabilitas Normal

Distribusi kurva normal dengan m sama dan s berbeda

Distribusi kurva normal dengan m berbeda dan s sama

Distribusi kurva normal dengan m dan s berbeda
Fungsi Denitas Distribusi Normal
Fungsi densitas distribusi normal diperoleh dengan persamaan sebagai berikut
dimana




π = 3,1416
e = 2,7183
µ = rata-rata
σ = simpangan baku
Persamaan di atas bila dihitung dan diplot pada grafik akan terlihat seperti pada Gambar
1 berikut.
Gambar 1. kurva distribusi normal umum
Sifat-sifat penting distribusi normal adalah sebagai berikut:
1.
2.
3.
4.
Grafiknya selalu berada di atas sumbu x
Bentuknya simetris pada x = µ
Mempunyai satu buah modus, yaitu pada x = µ
Luas grafiknya sama dengan satu unit persegi, dengan rincian
1. Kira-kira 68% luasnya berada di antara daerah µ – σ dan µ + σ
2. Kira-kira 95% luasnya berada di antara daerah µ – 2σ dan µ + 2σ
3. Kira-kira 99% luasnya berada di antara daerah µ – 3σ dan µ + 3σ
Membuat kurva normal umum bukanlah suatu pekerjaan yang mudah. Lihat saja rumus
untuk mencari fungsi densitasnya (nilai pada sumbu Y) begitu rumit. Oleh karena itu,
orang tidak banyak menggunakannya.
Orang lebih banyak menggunakan DISTIBUSI NORMAL BAKU. Kurva distribusi normal
baku diperoleh dari distribusi normal umum dengan cara transformasi nilai x menjadi
nilai z, dengan formula sbb:
Kurva distribusi normal baku disajikan pada Gambar 2 berikut ini.
Gambar 2. Kurva distribusi normal baku
Kurva distribusi normal baku lebih sederhana dibanding kurva normal umum. Pada
kurva distribusi normal baku, nilai µ = 0 dan nilai σ=1, sehingga terlihat lebih
menyenangkan. Namun, sifat-sifatnya persis sama dengan sifat-sifat distribusi normal
umum.
Untuk keperluan praktis, para ahli statistika telah menyusun Tabel distribusi normal baku
dan tabel tersebut dapat ditemukan hampir di semua buku teks Statistika. Tabel
distribusi normal bakui disebut juga dengan Tabel Z dan dapat digunakan untuk mencari
peluang di bawah kurva normal secara umum, asal saja nilai µ dan σ diketahui. Sebagai
catatan nilai µ dan σ dapat diganti masing-masing dengan nilai dan S.
Berikut adalah tabel distribusi normal standar, untuk P (X < x), atau dapat diilustrasikan
dengan luas kurva normal standar dari X = minus takhingga sampai dengan X = x.
Tabel Z
Contoh penggunaan tabel Z:
Hitung P (X<1,25)
Penyelesaian: Pada tabel, carilah angka 1,2 pada kolom paling kiri. Selanjutnya, carilah
angka 0,05 pada baris paling atas. Sel para pertemuan kolom dan baris tersebut
adalah 0,8944.
Dengan demikian, P (X<1,25) adalah 0,8944.
Contoh kasus menggunakan rumus Z
Rata-rata produktivitas padi di Aceh tahun 2009 adalah 6 ton per ha, dengan simpangan
baku (s) 0,9 ton. Jika luas sawah di Aceh 100.000 ha dan produktivitas padi
berdistribusi normal (data tentatif), tentukan
1. berapa luas sawah yang produktivitasnya lebih dari 8 ton ?
Jawab:
1. Hitung nilai z dari nilai x = 8 ton dengan rumus
2. Hitung luas di bawah kurva normal pada z = 2,22. Caranya buka Tabel Z dan lihat
sel pada perpotongan baris 2,20 dan kolom 0,02. Hasilnya adalah angka 0,98679 dan
bila dijadikan persen menjadi 98,679%. Angka ini menunjukkan bahwa luas di bawah
kurva normal baku dari titik 2,22 ke kiri kurva adalah sebesar 98,679%. Karena luas
seluruh di bawah kurva normal adalah 100%, maka luas dari titik 2,22 ke kanan kurva
adalah 100% – 98,679% = 1,321% (arsir warna hitam pada gambar). Oleh karena itu,
luas sawah yang produktivitasnya lebih dari 8 ton adalah 1,321%, yaitu (1,321/100) x
100.000 ha = 1321 ha.