Distribusi Normal

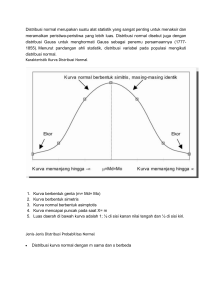
Distribusi
Normal
Kelompok 7
1.
2.
3.
4.
Uzlifatil Jannah
(17610020)
Windiar Hanin Nabilana
(17610024)
Najmi Nurul Illahi
(17610064)
Unzila Nur Laili
(17610092)
2
Pengertian
Apa itu Distribusi Normal?
Distribusi Normal merupakan distribusi yang simetris dan berbentuk genta atau lonceng
serta distribusi yang paling banyak digunakan dalam statistika untuk menaksir dan
meramalkan peristiwa-peristiwa yang lebih luas.
Distribusi ini juga dikenal sebagai “Distribusi Gauss“ untuk menghormati penemu
persamaannya yaitu Carl Gauss.
Dalam hal apa Distribusi Normal biasanya diterapkan?
Distribusi normal diterapkan dalam berbagai permasalahan seperti menerangkan fenomena
alam, industri, perdagangan, tingkat pendapatan masyarakat, dan sebagainya. Dua
parameter yang menentukan distribusi normal adalah rataan / ekspektasi (𝜇) dan standar
deviasi (𝜎).
3
Karakteristik Distribusi Normal



Kurva berbentuk genta atau lonceng dan memiliki satu puncak
yang terletak di tengah
Nilai rata-rata = median = modus yang memberikan pola simetris
Distribusi probabilitas dan kurva normal berbentuk kurva simetris
dengan rata-rata hitungnya (𝜇)
Karakteristik Distribusi Normal



Kurva ini menurun di kedua arah yaitu ke kanan untuk nilai positif
tak terhingga dan ke kiri untuk nilai negatif tak terhingga
Ujung-ujung sisi kurvanya sejajar dengan sumbu horizontal
(Sumbu X)
Luas daerah yang terletak di bawah kurva normal tetapi di atas
sumbu mendatar sama dengan 1.
Karakteristik Distribusi Normal



1
1
Mempunyai titik tertinggi 0,
dengan
=0,4
2𝜋
2𝜋
Sebagian besar data ada ditengah-tengah dan sebagian kecil ada
pada masing-masing sisi/tepi.
68% data berada dalam jarak ± 1 standar deviasi ,
95% data berada dalam jarak ± 2 standar deviasi,
99% data berada dalam jarak ± 3 standar deviasi.
Fungsi Kepadatan Peluang
Sebuah variabel acak kontinu X dikatakan memiliki distribusi normal dengan
parameter 𝜇 dan 𝜎 bila fungsi kepadatan peluang dari X adalah:
𝑓 𝑥 =
𝑥−𝜇
1
−1/2( 𝜎 )2
𝑒
, untuk −∞ < 𝑥 < ∞; 𝜎 > 0; −∞ < 𝜇 < ∞
𝜎 2𝜋
atau
1
1 𝑥−𝜇
𝑓 𝑥 =
exp −
2
𝜎
𝜎 2𝜋
7
2
Fungsi Kepadatan Kumulatif
Fungsi kepadatan kumulatif didefinisikan sebagai peluang variabel acak normal X bernilai
kurang dari atau sama dengan suatu nilai x tertentu. Maka fungsi kepadatan kumulatif dari
distribusi normal ini dinyatakan sebagai :
𝑥
𝐹 𝑥 =𝑃 𝑋≤𝑥 =
𝑥
𝑓 𝑡 𝑑𝑡 =
−∞
−∞
Keterangan :
>
>
>
>
𝜋 = 3,1416 …
𝑒 = 2,7183 …
𝜇 = rata-rata distribusi
𝜎 = simpangan baku
8
1
𝜎 2𝜋
𝑒 −1/2(
𝑡−𝜇 2
)
𝜎
𝑑𝑡
Parameter
Fungsi Pembangkit Momen
𝑀x(𝑡) =
1
𝜇𝑡+ 𝜎2 𝑡 2
𝑒 2
Nilai Ekspektasi
Jika 𝑋 adalah peubah acak bebas yang terdistribusi normal, maka 𝐸(𝑋)=𝜇.
Variansi
Jika 𝑋 adalah peubah acak bebas yang terdistribusi normal, maka 𝑉𝑎𝑟(𝑋)=𝜎 2 .
9
Contoh Soal 1
Dalam suatu ujian terdapat 300 siswa yang mengikuti ujian tersebut.
Rata-rata dari hasil ujian yaitu 70 serta simpangan baku hasil ujian
tersebut adalah 10. Jika data nilai hasil ujian siswa tersebut berdistribusi
normal, maka berapa persen mahasiswa yang mendapat nilai A jika
syarat untuk mendapatkan nilai A adalah nilai lebih dari 85.
Diket:
µ = 70,
σ = 10,
x = 85
Ditanyakan: Z(X>85)?
10
Contoh Soal 1
Jawab:
Z(X > 85) = 1 – Z(X < 85)
Akan dihitung terlebih dahulu nilai dari Z (X < 85)
Z = (x – µ)/σ = (85 – 70)/10 = 15/10 = 1,5
Nilai Z untuk 1,50 adalah 0,9332
sehingga
Z(X > 85) = 1 – Z(X < 85)
Z(X > 85) = 1 – 0,9332
Z(X > 85) = 0,0668
Z(X > 85) = 6,68%
11
Contoh Soal 2
Variabel X distribusi normal dengan mean 50 dan standard deviasi =10.
Carilah probabilitas untuk menemukan X bernilai antara 45 dan 62?
Diketahui:
μ = 50,
σ=10,
𝑥1 = 45,
𝑥2 =62
𝑧1 = (𝑥1 -μ)/σ  𝑧1 = (45-50)/10 = -0.5
𝑧2 = (𝑥2 -μ)/σ  𝑧2 = (62-50)/10 = 1.2
Ditanya: P(45 <x< 62)?
12
Contoh Soal 2
Jawab:
P(45 <x< 62) = P(45-50/10 < (x – µ)/σ < (62-50)/10
= P(-0.5<z<1.2)
P(-0.5<z<1.2) = P(z<1.2) – P(z<-0.5)
= 0.8849-0.3085
=0.5764
13
- Sekian -
“Bagi yang masih bingung
boleh bertanya. Bagi yang
sudah paham, kami mohon
bantuannya. ”
15
Mohon Maaf dan Terima Kasih

Wassalamu’alaikum
16