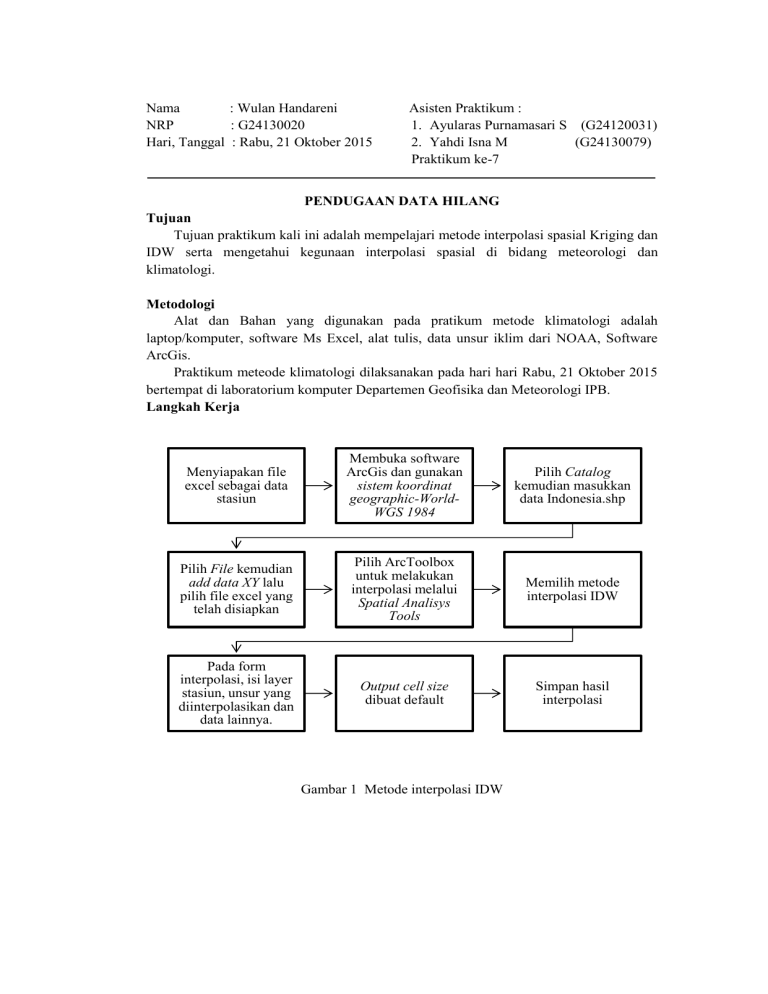
Nama : Wulan Handareni NRP : G24130020 Hari, Tanggal : Rabu, 21 Oktober 2015 Asisten Praktikum : 1. Ayularas Purnamasari S (G24120031) 2. Yahdi Isna M (G24130079) Praktikum ke-7 PENDUGAAN DATA HILANG Tujuan Tujuan praktikum kali ini adalah mempelajari metode interpolasi spasial Kriging dan IDW serta mengetahui kegunaan interpolasi spasial di bidang meteorologi dan klimatologi. Metodologi Alat dan Bahan yang digunakan pada pratikum metode klimatologi adalah laptop/komputer, software Ms Excel, alat tulis, data unsur iklim dari NOAA, Software ArcGis. Praktikum meteode klimatologi dilaksanakan pada hari hari Rabu, 21 Oktober 2015 bertempat di laboratorium komputer Departemen Geofisika dan Meteorologi IPB. Langkah Kerja Menyiapakan file excel sebagai data stasiun Membuka software ArcGis dan gunakan sistem koordinat geographic-WorldWGS 1984 Pilih Catalog kemudian masukkan data Indonesia.shp Pilih File kemudian add data XY lalu pilih file excel yang telah disiapkan Pilih ArcToolbox untuk melakukan interpolasi melalui Spatial Analisys Tools Memilih metode interpolasi IDW Pada form interpolasi, isi layer stasiun, unsur yang diinterpolasikan dan data lainnya. Output cell size dibuat default Simpan hasil interpolasi Gambar 1 Metode interpolasi IDW Menyiapakan file excel sebagai data stasiun Membuka software ArcGis dan gunakan sistem koordinat geographic-WorldWGS 1984 Pilih Catalog kemudian masukkan data Indonesia.shp Pilih File kemudian add data XY lalu pilih file excel yang telah disiapkan Pilih ArcToolbox untuk melakukan interpolasi melalui Spatial Analisys Tools Memilih metode interpolasi Krigging Pada form interpolasi, isi layer stasiun, unsur yang diinterpolasikan dan data lainnya. Output cell size dibuat default Simpan hasil interpolasi Gambar 2 Metode interpolasi Kriging Pembahasan Untuk keperluan penyusunan model suatu fenomena di satu wilayah diperlukan data beberapa komponen data pendukung. Pada kenyataannya, sering kali seorang peneliti dihadapkan pada ketidaklengkapan data yang diperlukan. Pertimbangan kondisi lingkungan, fisiografis, keterbatasan data dari berbagai titik di permukaan bumi ini dapat menghambat penyusunan model. Selanjutnya untuk menyusun suatu model yang baik disiasati dengan melakukan intepolasi. Interpolasi merupakan suatu metode atau fungsi matematika untuk menduga nilai pada lokasi-lokasi yang datanya tidak tersedia. Menurut Burrough and McDonell (1998), interpolasi adalah proses memprediksi nilai pada suatu titik yang bukan merupakan titik sampel, berdasarkan pada nilai-nilai dari titik-titik di sekitarnya yang berkedudukan sebagai sampel. Penentuan nilai baru didasarkan pada data yang ada pada titik-titik sampel. Tanpa adanya langkah interpolasi ini, maka analisis spasial tidak dapat dilakukan secara akurat. Ada beberapa metode yang dapat digunakan untuk melakukan interpolasi spasial. Menurut Demers (2000), interpolasi spasial dapat diklasifikasikan menjadi tiga, yakni global and local interpolation, exact interpolation and inexact interpolation, deterministic and stochastic interpolation. Diantara metode deterministik yang populer adalah Trend, Spline, Inverse Distance Weighted (IDW) dan Kriging. Praktikum kali ini akan dibahas penggunaan metode IDW dan Kriging untuk kajian curah hujan. Metode IDW dapat dikelompokkan ke dalam estimasi determenistik, yakni interpolasi dilakukan berdasarkan perhitungan matematika. Sementara metode Kriging dapat digolongkan ke dalam estimasi stochastik, di mana perhitungan secara statistik digunakan untuk menghasilkan interpolasi (Pramono 2008). Metode IDW merupakan metode interpolasi konvesional yang memperhitungkan jarak sebagai bobot. Jarak yang dimaksud disini adalah jarak (datar) dari titik data (sampel) terhadap blok yang akan diestimasi. Jadi semakin dekat jarak antara titik sampel dan blok yang akan diestimasi maka semakin besar bobotnya, begitu juga sebaliknya. Interpolasi stochastic menawarkan penilaian kesalahan dengan nilai prediksi. Metode ini mengasumsikan kesalahan acak. Contoh model ini yang populer adalah metode Kriging. Metode Kriging merupakan estimasi stochastik yang mirip dengan IDW, menggunakan kombinasi linear dari weights untuk memperkirakan nilai di antara sampel data. Metode ini dikembangkan oleh D.L. Krige untuk memperkirakan nilai dari bahan tambang. Asumsi dari model ini adalah jarak dan orientasi antara sampel data menunjukkan korelasi spasial. Model ini memberikan ukuran error dan confidence. Model ini juga menggunakan semivariogram yang merepresentasikan perbedaan spasial dan nilai diantara semua pasangan sampel data. Semivarogram ini menunjukkan bobot (weights) yang digunakan dalam interpolasi (Hadi 2013). Penentuan hasil pada metode IDW berdasarkan pada asumsi bahwa nilai atribut z (nilai yang diestimasi) pada titik yang tidak didata adalah merupaka fungsi jarak dan nilai rata-rata titik yang berada disekitarnya. Hasil interpolasi tergantung dari seberapa kuat sebuah titik data yang diketahui mempengaruhi daerah di sekitarnya. Selain itu juga jumlah titik di sekitarnya yang digunakan untuk menghitung rata-rata nilai, serta ukuran pixel/raster yang dikehendaki. Sedangkan penentuan hasil pada metode Kriging berdasarkan asumsi bahwa setiap titik di dalam bentang alam saling berhubungan dan mempunyai sebuah trend. Trend (persamaan matematis) yang digunakan untuk memprediksi titik yang tidak memiliki data/informasi. Sumber data yang digunakan praktikum kali ini berasal dari NOAA. Data stasiun yang digunakan untuk interpolasi adalah 41 stasiun cuaca yang tersebar di Indonesia, mulai dari Pulau Sumatera, Jawa, Kalimantan, Sulawesi, Nusa Tenggara, sampai Papua (nama stasiun terlampir). Unsur iklim yang diinterpolasikan adalah curah hujan. Gambar 3 Interpolasi metode IDW Gambar diatas adalah hasil interpolasi data curah hujan menggunakan metode IDW dengan cakupan wilayah Pulau Jawa, Nusa Tenggara, Provinsi Sulawesi Selatan dan Tenggara, Sumatera selatan hingga Lampung, Kalimantan Tengah dan Selatan, Maluku, serta Papua Barat dan Tengah. Dapat dilihat bahwa interpolasi menggunakan metode IDW menghasilkan nilai dengan cakupan wilayah yang lebih luas. Nilai interpolasi akan lebih mirip pada data sampel yang berdekatan lokasinya daripada data yang lokasinya lebih jauh. Karena metode ini menggunakan rata-rata dari data sampel sehingga nilainya tidak bisa lebih kecil dari minimum atau lebih besar dari data sampel. Jadi, puncak bukit atau lembah terdalam tidak dapat ditampilkan dari hasil interpolasi model ini (Watson dan Philip 1985). Untuk mendapatkan hasil yang baik, sampel data yang digunakan harus rapat yang berhubungan dengan variasi lokal. Jika sampelnya agak jarang dan tidak merata, hasilnya kemungkinan besar tidak sesuai dengan yang diinginkan. Gambar 4 Interpolasi metode Kriging Gambar diatas adalah hasil interpolasi data curah hujan menggunakan metode Kriging di wilayah yang sama dengan metode sebelumnya. Hasil interpolasi nampak berbeda dari metode IDW. Pada interpolasi kriging cakupan wilayah interpolasi lebih sempit. Pada jarak yang dekat (sumbu horisontal), semivariance bernilai kecil, tetapi pada jarak yang lebih besar, semivariance bernilai tinggi yang menunjukkan bahwa variasi dari nilai z tidak lagi berhubungan dengan jarak sampel point. Metode lain yang dapat digunakan untuk menginterpolasi data adalah Interpolasi tetangga terdekat (Nearest Neighbor Interpolation). Nearest Neighbor adalah metode paling sederhana dan pada dasarnya membuat piksel lebih besar. Warna pixel dalam gambar yang baru adalah warna dari piksel terdekat dari gambar asli. Pada interpolasi nearest neighbour (tetangga terdekat), nilai keabuan titik hasil diambil dari nilai keabuan pada titik asal yang paling dekat dengan koordinat hasil perhitungan dari transformasi spasial. Untuk citra 2 dimensi, tetangga terdekat dipilih di antara 4 titik asal yang saling berhubungan satu sama lain. Ada pula metode interpolasi Spline. Spline adalah metoda interpolasi yang biasa digunakan untuk mendapatkan nilai melalui kurva minimum antara nilai-nilai input. Metode ini baik digunakan dalam membuat permukaan seperti ketinggian permukaan bumi, ketinggian muka air tanah, ataupun konsentrasi polusi udara. Kurang bagus untuk siatuasi dimana terdapat perbedaan nilai yang signifikan pada jarak yang sangat dekat. Jika dipilih metoda Spline maka ada pilihan tipe Regularized dan Tension. Regularized membuat permukaan halus sedangkan Tension mempertegas bentuk permukaan sesuai dengan fenomena model. ESRI (1996) menyatakan bahwa metode interpolasi spline mengestimasinilai sel berdasarkan nilai rata-rata pada hampiran antara point data masing-masing contoh. Poligon Theissen juga salah satu metode interpolasi lokal. Metode ini disebut juga metode proximal merupakan suatu upaya memberikan bobot data titik-titik di suatu area. Sebagai contoh untuk interpolasi lokal untuk data presipitasi. Langkahnya adalah sejumlah segitiga digambar dengan cara menghubungkan titik-titik kontrol (misalnya, stasiun meteorologi) menggunakan teknik triangulasi Delaunay (juga digunakan untuk TIN). Garis ditarik tegak lurus terhadap sisi segitiga di titik tengah. Poligon didefinisikan oleh persimpangan (interaksi) dari garis-garis. Nilai-nilai untuk titik kontrol ditugaskan untuk merepresentasikan poligon (Hadi 2013). Kesimpulan Interpolasi spasial dibutuhkan dalam bidang meteorologi dan klimatologi untuk mengatasi terbatasnya data, lingkungan, serta kondisi fisiografis lainnya. Sehingga pemodelan unsur iklim tetap dapat dilakukan. Metode interpolasi IDW memberikan hasil interpolasi yang lebih akurat dari metode Kriging. Hal ini dikarenakan semua hasil dengan metode IDW memberikan nilai mendekati nilai minimum dan maksimum dari sampel data. Sedang metode Kriging terkadang memberikan hasil interpolasi dengan kisaran yang rendah. Daftar Pustaka Burrough PA and McDonnell RA. 1998. Principles Of Geographical Information System. London (UK) : Oxford University Press Inc. Demers and Michael N. 2000. Fundamentals of Geographic Information System Second Edition. New York(US) : Jhon Wiley and Sons. ESRI. 1996. Using the ArcView Spatial Analyst. Redlands (US) : Environmental Systems Research Institute, Inc Hadi BS. 2013. Metode Interpolasi Spasial dalam Studi Geografi. J Geomedia. Vol 11(2):231-240. Pramono dan Gatot H. 2008. Akurasi Metode IDW dan Kriging untuk Interpolasi Sebaran Sedimen Tersuspensi. Forum Geografi. Vol. 22(1):97-110. Watson DF & Philip GM. 1985. A Refinement of Inverse Distance Weighted Interpolation. J Geo Processing. Vol 2: 315-327. LAMPIRAN Tabel 1 Data curah hujan dari berbagai stasiun yang digunakan LONGITUDE LATITUDE STATION_NAME TPCP STATION 120,333 -9,667 WAINGAPU MAU HAU ID 50 GHCND:ID000097340 116,267 -8,75 MATARAM LOMBOK INTERNATIONAL AIRPORT ID 1191 GHCND:IDM00097240 115,167 -8,749 DENPASAR NGURAH RAI ID 790 GHCND:IDM00097230 122,237 -8,641 WAI OTI ID 434 GHCND:IDM00097300 118,687 -8,54 MUHAMMAD SALAHUDDIN ID 660 GHCND:IDM00097270 117,412 -8,489 SUMBAWA BESAR ID 521 GHCND:IDM00097260 114,383 -8,217 BANYUWANGI ID 717 GHCND:IDM00096987 124,567 -8,217 ALOR MALI KALABAHI ID 127 GHCND:IDM00097320 131,3 -7,983 SAUMLAKI OLILIT ID 578 GHCND:ID000097900 109,017 -7,733 CILACAP ID 360 GHCND:ID000096805 112,787 -7,38 SURABAYA JUANDA ID 2077 GHCND:IDM00096935 112,717 -7,217 SURABAYA PERAK ID 607 GHCND:IDM00096933 113,967 -7,05 KALIANGET MADURA IS 414 GHCND:IDM00096973 110,375 -6,973 ACHMAD YANI ID 1531 GHCND:IDM00096839 110,417 -6,967 SEMARANG ID 20 GHCND:IDM00096837 109,15 -6,85 TEGAL ID 2392 GHCND:IDM00096797 108,267 -6,75 CIREBON JATIWANGI ID 241 GHCND:IDM00096791 106,933 -6,7 BOGOR CITEKO ID 658 GHCND:IDM00096751 106,57 -6,293 BUDIARTO ID 114 GHCND:IDM00096739 106,833 -6,183 JAKARTA OBSERVATORY ID 3 GHCND:ID000096745 106,656 -6,126 SOEKARNO HATTA INTERNATIONAL ID 725 GHCND:IDM00096749 106,133 -6,117 SERANG ID 524 GHCND:IDM00096737 106,867 -6,1 JAKARTA TANJUNG PRIOK 361 GHCND:IDM00096741 112,633 -5,85 SANGKAPURA BAWEAN ID 2792 GHCND:ID000096925 132,75 -5,683 TUAL DUMATUBUN 361 GHCND:IDM00097810 122,617 -5,467 BAU BAU BETO AMBIRI ID 142 GHCND:IDM00097192 119,55 -5,067 UJANG PANDANG PAOTERE ID 2440 GHCND:IDM00097182 119,554 -5,062 HASANUDDIN ID 1967 GHCND:IDM00097180 138,95 -4,067 WAMENA ID 351 GHCND:ID000097686 102,339 -3,864 FATMAWATI SOEKARNO ID 531 GHCND:IDM00096253 128,083 -3,7 AMBON PATTIMURA ID 124 GHCND:ID000097724 114,763 -3,442 SYAMSUDIN NOOR ID 1075 GHCND:IDM00096685 104,701 -2,898 SULTAN MAHMUD BADARUDDIN II ID 1333 GHCND:IDM00096221 132,25 -2,883 FAK FAK TOREA ID 41 GHCND:IDM00097630 107,755 -2,746 H AS HANANDJOEDDIN ID 91 GHCND:IDM00096249 111,673 -2,705 ISKANDAR ID 635 GHCND:IDM00096645 120,367 -2,55 MASAMBA ANDI JEMMA ID 1201 GHCND:IDM00097126 119 -2,5 MAJENE 121 GHCND:IDM00097120 113,943 -2,225 TJILIK RIWUT ID 1047 GHCND:IDM00096655 106,13 -2,17 PANGKALPINANG ID 147 GHCND:IDM00096237