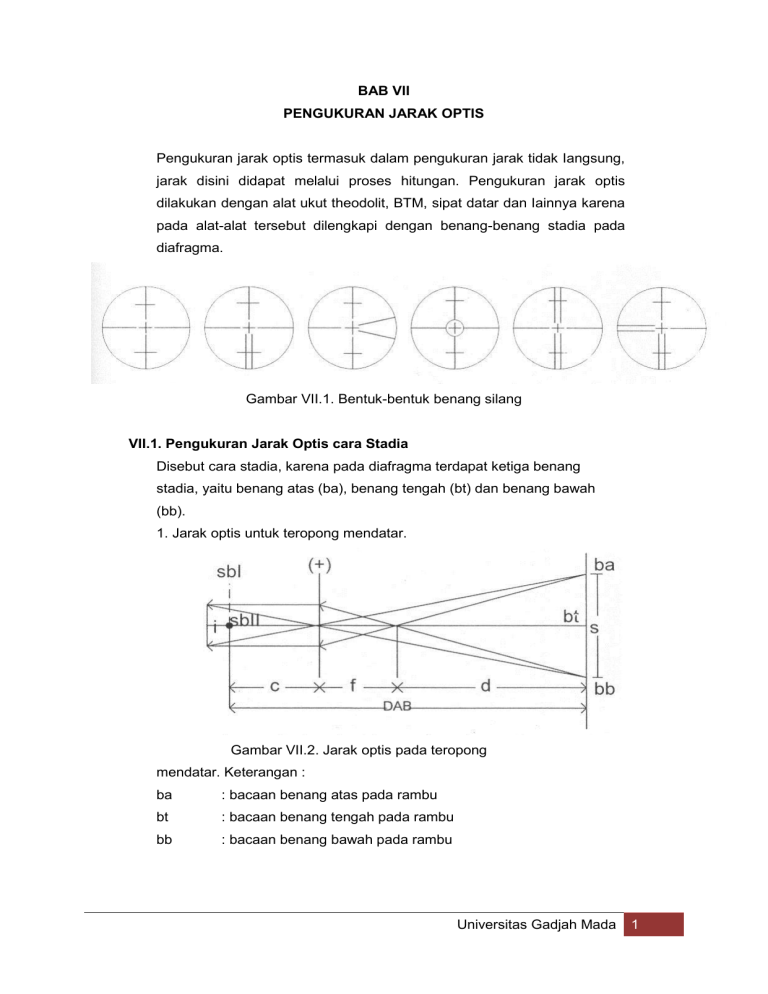
BAB VII PENGUKURAN JARAK OPTIS Pengukuran jarak optis termasuk dalam pengukuran jarak tidak Iangsung, jarak disini didapat melalui proses hitungan. Pengukuran jarak optis dilakukan dengan alat ukut theodolit, BTM, sipat datar dan Iainnya karena pada alat-alat tersebut dilengkapi dengan benang-benang stadia pada diafragma. Gambar VII.1. Bentuk-bentuk benang silang VII.1. Pengukuran Jarak Optis cara Stadia Disebut cara stadia, karena pada diafragma terdapat ketiga benang stadia, yaitu benang atas (ba), benang tengah (bt) dan benang bawah (bb). 1. Jarak optis untuk teropong mendatar. Gambar VII.2. Jarak optis pada teropong mendatar. Keterangan : ba : bacaan benang atas pada rambu bt : bacaan benang tengah pada rambu bb : bacaan benang bawah pada rambu Universitas Gadjah Mada 1 c : jarak sumbu II — lensa obyektif f : jarak fokus lensa obyektif : jarak ba — bb pada diafragma s : jarak ba — bb pada rambu d : jarak dari fokus rambu DAB : jarak datar dari A — B Dari gambar diatas didapat hubungan : DAB=c+f+d Jika d:s = f:i DAB=c+f+ Jika = = A = konstante pengali teropong harganya 100 C + f = B = konstante penambah DAB =A.S+B Maka didapat rumus jarak optis pada teropong mendatar/ garis bidik mendatar : DAB=A.S+B .................................... (1) 2.Jarak optis untuk teropong miring. Kemiringan teropong atau garis bidik sebesar sudut miring a, dapat digambarkan : Gambar VII.3. Jarak optis pada teropong miring. Dari gambar diatas, didapat hubungan : DAB = TM cos a TM=A.S1+B DAB = (A. S1 + B) cos a S1 = S cos a Universitas Gadjah Mada 2 DAB = A. S cos2 a + B cos a (2) Catatan : Harga koustante B karena mendekati nol, maka rumus tersebut dapat Iebih sederhana. Sudut miring a dicari dari a = 90° — Z .......................................... (3) Z adalah sudut zenith yang dibaca pada piringan vertikal theodolit. Contoh : Dad gambar diatas, didapat data bacaan bt = 1000; ba = 1527; bb = 0473; sudut zenith Z = 88°30'25" Hitung jarak AB Hitungan : a = 90° — 88° 3025" = 1°29'35" dari rumus (2) D = AS Cos2 a = 100(1527-0473)cos2 1° 29'35" = 105.328 m pada pengukuran jarak optis, dikenal pengukuran takhimetri atau tachymetry, yaitu pengukuran jarak datar dan beda tinggi dengan pembacaan benang stadia pada rambu serta sudut miring teropong. Gambar VII.4 takhimetri Dari gambar VII.4. didapat hubungan : DAB = A.S Cos2 .................................... (2) V = DAB tg ........................................... (4) HAB=V + ti - bt ........................................ (5) Rumus (5) adalah rumus untuk menghitung beda tinggi antara titik A dan B. Universitas Gadjah Mada 3 VII.2. Pengukuran Jarak cara Tangensial Pada pengukuran tangensial, tidak dibaca benang-benang ba dan bb, tetapi hanya benang tengah (bt) saja. Gambar VII.5 pengukuran jarak secara tangensial Dari gambar didapat hubungan persamaan : DE = DAB tg CE = DAB tg h DE-CE = DAB (tg -tg h) S = DAB tg (a - h) DAB = ............................ (6) Rumus (6) adalah rumus jarak optis cara tangensial VII.3 Pengukuran Jarak Optis dengan Subtense bar Subtanse bar/ batang ukur jarak adalah rambu khusus terbuat dari invar, panjang 2m dan dilengkapi dengan alat pengincar. Gambar VII.6. batang ukur jarak dari kern Universitas Gadjah Mada 4 Dengan mengukur sudut horisontal antara ujung batang theodolit dan ujung batang dapat ditentukan jarak mendatarnya. Gambar VII.7. Geometri pengukuran Subtanse bar. DAB = DAB = ........................................ (7) Universitas Gadjah Mada 5 BAB VIII PENGUKURAN SUDUT HORISONTAL Sudut horisontal adalah sudut yang diperoleh dengan mengurangkan bacaan arah horisontal piringan mendatar suatu theodolit. Ada tiga syarat dasar menentukan sudut, yaitu : 1. garis awal/ acuan 2. Arah putaran 3. Jarak sudut/ besar sudut Pengukuran sudut horisontal dapat dilakukan dengan : 1. cara reiterasi 2. cara repetisi VIII.1. Alat ukur sudut Sudut horisontal dapat diukur dengan alat ukur sudut/ arah, seperti : a. theodolit b. kompas c. theodolit kompas ketiga alat tersebut dapat dipakai untuk mengukur sudut, karena adanya piringan horisontal yang berpembagian skala/ skala cara pengukuran sangat terkait dengan konstruksi sumbu I theodolit, yaitu theodolit reiterasi dari theodolit repetisi. VIII. 2. Pengukuran Sudut cara reiterasi Gambar VIII.1. cara reiterasi Universitas Gadjah Mada 6 Pada pengukuran sudut cara reiterasi ini, pengukuran dimuka dengan kedudukan teropong BIASA, diarahkan ke titik 1 dibaca arahnya selanjutnya diputar terhadap sumbu I diarahkan ke titik 2, dibaca arahnya. Setelah arah ke 2, dilanjutkan ke titik 3 dan titik 4. Dari arah ketitik 4, Kemudian teropong diputar balik menjadi kedudukan teropong LUAR BIASA. Pengukuran dimulai diarahkan ke titik 4, titik 3 sampai berakhir di titik 1. pengukuran sudut dari 1 ke titik 4 dengan teropong BIASA dan kembali dari titik 4 kembali ke titik 1 dengan teropong LUAR BIASA disebut pengukuran satu seri. Bila akan diukur n seri, maka ada pergeseran arah sebesar 180° : n pada tiap seri. Misal akan diukur sudut tersebut diatas sebanyak 3 seri; ini berarti ada pergeseran arah sebesar 180° : 3 = 60° Maka pada : Seri I dimulai dengan 0° Seri II dimulai dengan 60° Seri III dimulai dengan 120° Sudut-sudut pada gambar diatas dihitung dari selisih dua arah yang berurutan. Cara reiterasi disebut sebagai cara pengukuran jurusan. VIII.3. Pengukuran sudut cara repetisi Gambar VIII.2. cara repetisi Pengukuran sudut cara repetisi ini pada dasarnya adalah pengukuran sudut yang berulang ditentukan besarnya kelipatan n sudut, sehingga besar sudut ada 1/n hasil pengukuran kelipatan sudut itu. Dengan n dinamakan repetisi. Pada cara ini, yang dicatat pembacaan arah pertama (1), pembacaan arah Universitas Gadjah Mada 7 kedua (2) dan pembacaan arah terakhir (n+1). Besar sudut dihitug dari persamaan : pendekatan = arah (2) — arah (1) ( ) ( ) Dengan P = berapa kali pembacaan arah melewati 360° atau ( ) Contoh : hasil pengukuran sudut cara repetisi Titik arah 1 1X2 Pembacaan arah Arah (2) Arah (n+1) 0 Keterangan Skala 360° 12 15' 05" 780 20' 25" dilewati 480 47' 10" 6X2 satukali VIII.4. Pengukuran sudut banyak cara Bessel dan cara Schreiber 1. Cara schreiber atau cara kombinasi Gambar VIII.3. Cara Schreiber Universitas Gadjah Mada 8 Pada cara screiber, dari r arah, akan diukur sudut sebanyak : 1/2r (r-1), dari gambar r = 4 maka jumlah sudut yang diukur = 1/2.4 (3) = 6 sudut. Sudut dapat diukur dengan cara repetisi atau cara reiterasi. 2. cara bassel Gambar VIII.4. cara Bessel Pengukuran sudut banyak cara bessel, dilakukan dengan cara reiterasi (metode arah). a. Pengukuran dari A menjadi B, C dan akhirnya ke A lagi (dengan kedudukan teropong BIASA) b. Selanjutnya teropong diputar balik menjadi kedudukan LUAR BIASA, pengukuran lebih di mulai dari A menuju E, D dan selanjutnya berakhir di A lagi. Universitas Gadjah Mada 9 BAB IX PERALATAN UKUR KETINGGIAN Beda tinggi antara dua titik dapat ditentukan dengan tiga cara: 1. Cara Barometris 2. Cara trigonametris 3. Cara menyipat datar Ketiga cara tersebut beda dalam peralatan dan tingkat ketelitian yang dicapai. IX.1. Alat Ukur Penyipat datar Alat ukur penyipat datar dapat diklasifikasi dari alat penyipat datar sederhana tanpa teropong : a. Alat penyipat datar sederhana, terdiri atas dua tabung gelas berdiri dan dihubungkan dengan pipa dari logam. b. Dua tabung gelas berskala yang dihubungkan dengan slang karet. c. Batang ukur A yang diberi nivo tabung dibuat mendatar dan mistar B yang berskala sampai dm. Alat penyipat datar optis yang dilengkapi teropong yang disebut sipat datar atau waterpas. Alat ukur sipat datar hanya dapat diputar pada sumbu I: Gambar IX.1. alat ukur penyipat datar sederhana. Universitas Gadjah Mada 10 IX.2. macam alat ukur sipat datar. 1. Alat Sipat datar tipe semua tetap terdiri dari : a. Tanpa skrup ungkit b. Dengan srup ungkit Alat-alat ini dilengkapi dengan dua macam nivo, yaitu nivo tabung dan nivo kotak adanya skrup pengungkit, dimungkinkan untuk menggerakkan teropong sedikit ke atas-bawah secara terbatas. Gambar IX.2. alat sipat datar tipe semua tetap tanpa dan dengan skrup pengungkit. 2. Alat sipat datar otomatis Disebut otomatis, karena apabila sumbu I telah vertikal maka garis bidik teropong akan mendatar. Hal tersebut karena pada alat tipe otomatis dilengkapi dengan peridukan atau kompensator, yang menggantikan fungsi nivo tabung. Alat sipat datar otomatis menjadi populer dalam pemakaiannya, karena kemudahan dan kecepatan operasinya. 3. Alat sipat datar dengan sinar laser 4. Alat sipat datar elektronik Universitas Gadjah Mada 11 Gambar IX.3. Beberapa sipat datar otomatis IX.3. syarat pemakaian alat ukur sipat data Sebelum alat dipakai untuk pengukuran dilapangan, maka diperlukan syarat pemakaian yang harus dipenuhi : 1. Syarat utama 2. Syarat kedu 3. Syarat ketiga : garis bidik teropong sejajar dengan garis arah nivo : garis arah nivo tegak lurus sumbu I : garis mendatar diafragma tegak lurus sumbu I Syarat kedua : garis arah nivo tegak lurus sumbu I, pada prinsipnya sama dengan mengatur sumbu I menjadi vertikal pada sebuah theodolit. Universitas Gadjah Mada 12 Syarat ketiga garis mendatar diafragma tegak lurus sumbu I, oleh pembidik pembuatannya telah dibuat tegak lurus sumbu I Syarat utama : garis bidik teropong sejajar dengan garis nivo Untuk syarat utama ini dilakukan percobaan sebagai berikut: Gambar IX.4. cek syarat utama Keterangan ao, bo, a2 b2 = bacaan bt dengan garis bidik mendatar a, b, a3,b3 = bacaan bt dengan garis bidik miring a = kemiringan garis bidik 1. Ditentukan titik A, I, B dan II dengan jarak antara sebesar Lm. 2. Dari kedudukan I, dibaca pada rambu A dan B harga bt. Masingmasing a, dan b1 3. Alat ukur sipat datar dipindah ke II dan dibaca bt pada rambu A, a3 dan rambu Bb3 4. Dari kedudukan I, beda tinggi AB Dad kedudukan II, beda tinggi AC 5. = H1 = al — b1 = H11 = a3 — b3 Jika H1= H11 berarti syarat utama balk A H1 # A H1I berarti syarat utama masih ada kemiringan sebesar kesalahan a3 a2 = C karena kemiringan garis bidik sebesar dihitung dengan persamaan C = ( HII- H1) Cara pemberian/ pelaksanaan koreksi Dari kedudukan II, teropong diarahkan ke pembacaan a3 — c dengan cara memutar skrup koreksi diafragma vertikal naik/turun. Ulangi angkah 2 s/d 5 sampai dicapai H1= H1I. Universitas Gadjah Mada 13 BAB X PEMETAAN PLANIMETRIS DENGAN PITA UKUR Xi. Pengantar Peta planimetris adalah peta yang menggambarkan posisi planimetris dari obyek yang diketahui. Umumnya peta ini digunakan untuk keperluan kadastral. Peta planimetris dibuat dengan skala besar 1 : 500 sampai 1 : 2500 Jika alat yang dipakai hanya pita ukur saja, termasuk pengadaan kerangka petanya maka luasan yang dipetakan hanya terbatas. X.2. Prosedur Pemetaan Planimetris Secara garis besar prosedur pemetaan planimetris adalah : 1. Pengadaan kerangka peta 2. Pengukuran detail dan pencatatannya 3. Penggambaran Pengadaan kerangka peta dan pengukuran detail sebetulnya dapat dilakukan secara bersamaan. X.3. bentuk-bentuk kerangka peta dan kontrolnya. 1. Rangkaian segitiga Gambar X.1. kerangka peta bentuk rangkaian segitiga. Universitas Gadjah Mada 14 2. Garis Baris Gambar X.2. Kerangka peta bentuk garis besar. 4. Garis pangkal Gambar X.3. Kerangka Peta bentuk garis pangkal. X.4. Pengukuran detail 1. Cara penyikuan Gambar X.4. pengukuran detail cara penyikuan Universitas Gadjah Mada 15 Pojok-pojok bangunan B diproyeksikan ke garis ukur 1 2 di titik-titik a1 dan b1 2. Cara pengikatan Gambar X.5. pengukuran detail cara pengikatan Pojok bangunan B, diikat dari titik-titik bantu a, b dan titik 2. Titik-titik bantu bisa ditentukan dulu pada garis ukur 1 2. 3. Cara interpolasi Gambar X.6. Pengukuran detail cara interpolasi Pada pengukuran detail cara interpolasi, sisi-sisi bangunan B diluruskan sampai di garis-garis ukur. Titik-titik potong yang terjadi 11, 31, 21, dan 41. Pengal-pengal garis yang terjadi diukur, agar dapat dipakai untuk menggambar posisi detail. Pada pengukuran detail pada umumnya dipakai cara kombinasi/ gabungan dari ketiga cara tersebut. X.5. Pencatatan data ukur. Pencatatan data ukur ditulis langsung pada sket yang dibuat dilapangan oleh karena itu skets dibuat dengan memakai skala besar dan dibuat secara rapi dan benar. Skets yang balk dan rapi akan sangat membantu dalam proses pengambaran. Penulisan data ukur, ditulis search jalanya pengukuran. Ketentuan penulisan jarak terukur ada tanda (-) atau ( ) yang berarti jarak Universitas Gadjah Mada 16 masih berlanjut. Tanda (=) berarti berhenti, disamping tanda (<>) untuk kontrol ukuran. Contoh 1: Jarak 1 ke 2 = 30.0+21.0 m 1 ke a = 16.1 m 1 ke b = 30.0 m contoh 2. Gambar X.8. penulisan angka diangsul Jarak diagonal 4-1 = 25.16 m, didalam tanda < > X.6. Pengambaran Pengambaran data-data ukur, dimulai dengan tahapan : 1. penggambaran kerangka peta dilanjutkan dengan ceking dengan kontrol ukuran. 2. Setelah penggambaran kerangka peta selesai, dilanjutkan dengan penggambran detail. 3. Pada penggambaran detail prinsipnya adalah merekontruksi kembali seperti saat pengukuran di lapangan. Peta yang dihasilkan di perhalus dan dilengakapi dengan legenda dan keterangan secukupnya. Universitas Gadjah Mada 17