silabus - Kuliah Online UNIKOM

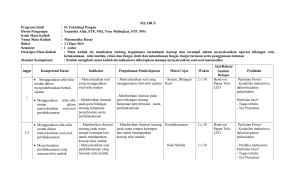
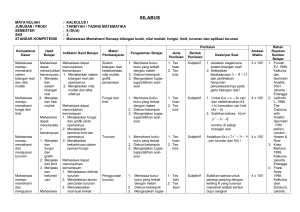
DESKRIPSI MATA KULIAH
Nama Mata Kuliah
:
Kalkulus I
Kode Mata Kuliah
:
IF31201
Kredit
:
3 SKS (3X45 menit)
Semester
:
I
Tingkat
:
I
Program Studi
:
Strata Satu
Jurusan
:
Teknik Informatika
Dosen
:
Inne Novita Sari, M.Si
Deskripsi :
Membahas mengenai sistem bilangan real, persamaan dan pertidaksamaan, limit dan
fungsi, turunan, integral tak tentu, dan teknik pengintegralan.
Referensi :
1. Martono, Koko. 1999. Kalkulus. Erlangga: Jakarta
2. Purcell & Vanberg. 1999. Kalkulus dan Geometri Analitik , edisi kelima, Erlangga:
Jakarta.
3. Spiegel, MR.2002. Kalkulus Lanjut, edisi kedua. Erlangga: Jakarta
Aturan Perkuliahan :
1. Kehadiran minimal perkuliahan adalah 80 % dari total pertemuan di kelas, kecuali sakit
atau ijin tertulis.
2. Tidak ada ujian perbaikan. Ujian susulan hanya diijinkan jika ada ijin autentik yang bisa
ditunjukkan setelah ujian.
3. Semua tugas harus dikerjakan dan diserahkan tepat pada waktu yang ditentukan. Semua
alasan keterlambatan yang tidak logis, tidak diterima dan nilai nol (0) bagi yang tidak
maupun terlambat menyerahkan.
4. Mahasiswa yang terlambat lebih dari 15 menit sebanyak 3 kali tidak diperkenankan
masuk ke kelas.
SILABUS
I. Identitas Mata Kuliah
1. Nama Mata Kuliah
: Kalkulus 1
2. Kode Mata Kuliah
: IF31201
3. Jurusan
: Teknik Informatika
4. Semester
: I
5. Bobot SKS
: 3 SKS
6. Dosen
: Inne Novita Sari, M.Si
II. Deskripsi Singkat Mata Kuliah
Mata Kuliah Kalkulus 1 ini membahas mengenai sistem bilangan real, persamaan dan
pertidaksamaan, limit dan fungsi, turunan, dan integral tak tentu.
III. Tujuan Instruksional Umum
Setelah menyelesaikan mata kuliah Kalkulus 1, mahasiswa akan dapat menyelesaikan
masalah-masalah fungsi, limit, menentukan turunan fungsi menggunakan limit,
mengaproksimasi suatu nilai dan mengintegralkan suatu fungsi.
IV. Metode Perkuliahan
1. Ceramah
2. Latihan
3. Tugas
4. Quiz
V. Nilai Akhir
NA = 10% Absen + 20%  Tugas / Quiz + 30%  UTS + 40%  UAS
NILAI
INDEKS
PREDIKAT
80  NA  100
A
LULUS, SANGAT BAIK
68  NA  79
B
LULUS, BAIK
56  NA  67
C
LULUS, CUKUP BAIK
45  NA  55
D
LULUS, KURANG
0  NA  44
E
TIDAK LULUS
VI. Materi Kuliah
PERTEMUAN
MATERI
KE
METODE
Sistem Bilangan Real
a. Definisi Sistem Bilangan
1
b. Sistem Bilangan Real
Ceramah
c. Hukum dan Teorema
Latihan
d. Angka Penting
e. Soal Latihan
Persamaan dan Pertidaksamaan
a. Definisi Persamaan
2
b. Jenis Persamaan
Ceramah
c. Definisi Pertidaksamaan
Latihan
d. Daerah Penyelesaian Pertidaksamaan
e. Soal Latihan
Fungsi
a. Definisi Relasi
b. Definisi Fungsi
3
c. Daerah Asal dan Daerah Hasil Fungsi
d. Definisi Fungsi Komposisi
Ceramah
Latihan
e. Daerah Asal dan Hasil Fungsi Komposisi
f. Soal Latihan
Fungsi (lanjutan)
a. Penggambaran Grafik Fungsi
4
b. Jenis Fungsi
Ceramah
Latihan
c. Fungsi Trigonometri
d. Soal Latihan
Limit
a. Definisi Limit
5
b. Teorema Limit
Ceramah
c. Limit dengan Substitusi
Latihan
d. Limit Trigonometri
e. Soal Latihan
Limit (lanjutan)
0 ∞
6
a. Limit dengan bentuk 0 , ∞
Ceramah
b. Operasi pada Limit
Latihan
c. Kekontinuan Fungsi
d. Soal Latihan
7
Review (Quiz)
8
UJIAN TENGAH SEMESTER (UTS)
Latihan
Turunan
a. Definisi Turunan
9
b. Notasi Turunan
Ceramah
c. Bentuk yang Setara
Latihan
d. Aturan pencarian turunan
e. Soal latihan
Turunan (lanjutan)
10
a. Turunan Trigonometri
Ceramah
b. Aturan Rantai
Latihan
c. Soal Latihan
Turunan (Lanjutan)
a. Notasi Leibniz
11
b. Turunan Tingkat Tinggi
Ceramah
c. Pendiferensialan Implisit
Latihan
d. Diferensial dan Aproksimasi
e. Soal Latihan
Penggunaan Turunan
a. Nilai Maksimum dan Minimum
b. Kemonotonan (monoton naik dan turun)
12
c. Kecekungan (cekung ke atas dan bawah)
d. Titik stationer
Ceramah
Latihan
e. Penggambaran Grafik canggih
a. Soal Latihan
Integral
a. Definisi Integral Tak Tentu
13
b. Sifat Integral tak tentu
a. Notasi Jumlah dan Sigma
Ceramah
Latihan
c. Soal latihan
Fungsi Transenden
a. Definisi Logaritma Asli
14
b. Fungsi Eksponen Asli
c. Fungsi Eksponen Umum
Ceramah
Latihan
d. Soal Latihan
15
Teknik Pengintegralan
Ceramah
a. Pengintegralan dengan Substitusi
Latihan
b. Integral Trigonometri
c. Substitusi yang Merasionalkan
d. Integral Parsial
e. Integral Fungsi Rasional
16
UJIAN AKHIR SEMESTER (UAS)
VII. DAFTAR PUSTAKA
1. Martono, Koko. 1999. Kalkulus. Erlangga: Jakarta
2. Purcell & Vanberg. 1999. Kalkulus dan Geometri Analitik , edisi kelima, Erlangga:
Jakarta.
3. Spiegel, MR.2002. Kalkulus Lanjut, edisi kedua. Erlangga: Jakarta