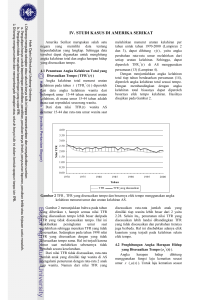
persamaan pertumbuhan von bertalanffy

PERTUMBUHAN
PERTUMBUHAN :
• Peningkatan biomas suatu populasi yang
dihasilkan oleh akumulasi bahan-bahan yang ada
dalam lingkungannya
• Perubahan panjang atau berat ikan selama waktu
tertentu
 Untuk menghitung pertumbuhan diperlukan
data L atau W dan umur atau waktu
• STUDI PERTUMBUHAN : penentuan ukuran
tubuh sebagai fungsi dari umur
 Semua studi pertumbuhan bekerja dengan
data komposisi umur
►Di daerah beriklim sedang, data komposisi umur
dapat diperoleh dari pengitungan lingkaran
tahunan.
► Di daerah tropis, tidak mungkin menggunakan
lingkaran tahunan untuk penentuan umur 
digunakan metode numerik ~ konversi dari
frekuensi panjang ke dalam komposisi umur.
1. POLA PERTUMBUHAN
Weatherley ’72 : pola pertumbuhan dibagi 4 :
1) Pertumbuhan larva (perubahan bentuk dan ukuran badan berubah
dengan cepat)
2) Fase Juvenile
3) Fase Linier (perubahan panjang dan berat terjadi secara linier, energi
dimanfaatkan untuk pertumbuhan dan perkembangan gonad)
4) Fase dewasa (energi dimanfaatkan untuk pemeliharaan)
2. ANALISIS PERTUMBUHAN
Tujuan analisis pertumbuhan dalam Dinpop adalah :
- Mengetahui pengaruh pertumbuhan terhadap waktu atau kapan
pertama kali bertelur
- Pengaruh laju pertumbuhan terhadap stok
- Pengaruh laju pertumbuhan terhadap potensi hasil suatu stok
↔
Dalam manajemen perikanan : memprediksi ukuran ikan
rata-rata pada beberapa titik waktu
3. KURVA PERTUMBUHAN
Pertumbuhan ikan sering digambarkan dengan bentuk
perubahan L atau W berdasarkan waktu yang dinyatakan
dengan matematika.
Von Bertalanffy = pertumbuhan panjang dan berat terhadap
waktu adalah berbeda.
- Jika L diplotkan terhadap waktu  kurva dengan sudut yang
semakin kecil dengan bertambahnya umur  garis kurva tersebut
mendekati asymptote atas yang sejajar dengan sumbu-x.
- Jika W diplotkan dengan umur  kurva berbentuk sigmoid —
peningkatan atau perubahan W pada tahap awal rendah atau lambat,
kemudian cepat dan menurun setelah mencapai titik infleksi.
Pertumbuhan terdiri dari 2 macam :
1) Pertumbuhan absolut (ukuran rata-rata ikan pada umur tertentu)
2) Pertumbuhan relatif (L/W dalam suatu periode dibandingkan dengan
L/W pada awal periode tersebut)
4. MODEL PERTUMBUHAN
Didesain untuk menerangkan dan menduga perubahanperubahan yang terjadi di dalam suatu populasi ikan dari
waktu ke waktu  sehingga berguna untuk mengambil
keputusan dalam pengelolaan sumber daya perikanan.
Terdapat 2 macam :
A. Model yang berhubungan dengan berat
B. Model yang berhubungan dengan panjang
 Model pertumbuhan yang berhubungan dengan panjang :
1) Model linier
 Lt = a + bt
2) Model logaritmik
 Lt = a + b log t
3) Model eksponensial
 Lt = a.bt
4) Model geometrik
 Lt = a.tb
5) Model Gompertz
 Lt = a.ebt
6) Model von Bertalanffy
 Lt = L ∞ (1-e-k (t-to))
PERSAMAAN PERTUMBUHAN
VON BERTALANFFY
 Merupakan dasar dalam bioper
 Digunakan sebagai suatu submodel dalam sejumlah model yang lebih
rumit dalam menjelaskan berbagai dinamika dari populasi ikan
 Gulland ’69 : terdapat hubungan linier antara kecepatan pertumbuhan
dan panjang ikan.
dL
dT
dL
dT
k (L∞ – L)..................................... (1)
L
L∞
k L∞ – k L
t
a
b
Lη = -a/b
Jika L= L∞
 dL
=0
dT
atau dalam bentuk persamaan differensial :
dL
= k dt
PENDEKATAN
LAIN VBGF
L  L
Dalam bentuk logaritma
dL
L' =- JL)– =K.ktL+ constanta
 Merupakan hubungan linier antara L' dan L
-Log=(L∞
dTatau, L∞ - L = e-kt x constanta
L
x - constanta x e-kt …………………………(2)
atau, y aL =b L∞
Dengan memasukkan to sebagai umur teoritis pada saat L=o maka didapat nilai
J
dL/dt
konstanta
sebagai
berikut
:
Solusi analitis persamaan diatas adalah sebagai berikut :
0 = L∞ - constanta x e-kto
atau, constanta = L∞ ekto
J
=
-K
(L
J/K
Selanjutnya :
K
L = L∞ - constanta x e-kt
dL
kto) x e-kt
L
=
L∞
(L∞
e
= -K dt
J
Maka : Lt = L∞*[1 – ek(t-to)] ↔ Persamaan Pertumbuhan von Bertalanffy
L
Wt = W∞[1 – e-k(t-to)]3
K
t
Bagaimana mengkonversi panjang ke umur?
dL
dT
Sehingga,

1
J
L
K
dL
=
  Kdt
  Kdt

1
L
J
K
dL
= -K.t + c
= In
+ c'
Ingat rumus :
dx
 x  a  = In (x+a) + konstanta
Sehingga,

1
J
L
K
dL
=
  Kdt
  Kdt

1
L
J
K
dL
= -K.t + c
= In
J 

L

K 

+ c'
Ingat rumus :
dx
 x  a  = In (x+a) + konstanta
Maka :
Ln  L 

J 

K 
+ C'= -k.t + C
Ln
J 

L

K 

= -k.t + C – C'
Ln
J 

L

K 

= -k.t + C''
L(t) = J
+ C '''.exp (-k.t) ; dimana C''' = exp (C'')
K
Diketahui bahwa Linf = J/K , maka
L(t) = Linf + C '''.exp (-k.t)…………………………………………………. (1)
Kondisi awal L=0 pada saat t=to, maka
L(to) = 0 = Linf + C '''.exp (-k.to)
Linf = C '''exp (-k.to)
C ''' = - Linf
C ''' = -Linf.exp (k.to) …………………… (2)
Exp (-k.to)
Memasukkan persamaan (2) ke dalam persamaan (1).
L(t) = Linf – Linf.exp (k-to).exp (-k.t)
L(t) = Linf [ 1 – exp (-K (t – to) ) ] ↔ Persamaan Pertumbuhan von
Bertalanffy
MODEL YANG BERHUBUNGAN DENGAN BERAT.
Massa = Densitas . Volume
M= (M/L3)(L3)
Pertumbuhan isometrik : W = a L3
Mengkombinasikan persamaan pertumbuhan isometrik dengan VBGF.
W = a L3 dan L(t) = Linf [ 1 – exp (-k (t – to) ) ]
Wt = a [ Linf [ 1 – exp ( -k (t-to))] ]3
Wt = Winf [ 1 – exp ( -k (t-to)) ] ↔ dimana Winf = a (Linf)3
Estimasi Parameter-Parameter Pertumbuhan Von Bertalanffy
1. FORD-WALFORD PLOT
Untuk mengkaji parameter pertumbuhan von Bertalanffy dari data yang
menggambarkan rentang waktu yang sama.
Didasarkan pada persamaan :
Lt = L∞ (1 – e-kt ) ………………………………………………………… (5)
Lt = L∞ - L∞ . e-kt
L∞ - Lt = L∞ . e-kt ………………………………………………………… (6)
Mengganti Lt dengan Lt+1 , maka
Lt+1 = L∞ ( 1 – e-k (t+1) ) …………………………………………………… (7)
Selisih persamaan (7) dengan persamaan (5) adalah :
Lt+1 – Lt = L∞ ( 1 – e-k(t+1) ) - L∞ ( 1 – e-kt )
= -L∞ . e-k(t+1) + L∞ . e-kt
Lt+1 – Lt = -L∞ . e-kt ( 1 – e-kt ) …………………………………………… (8)
Memasukkan persamaan (6) ke dalam persamaan (8), maka
Lt+1 – Lt = ( L∞ - Lt ) ( 1 – e-kt )
Lt+1 – Lt = L∞ ( 1 – e-k ) – ( Lt + Lt . e-k )
Lt+1 = L∞ ( 1 – e-k ) + ( Lt . e-k ) …………………………………………… (9)
y
a
b
Sehingga :
K = -In (b) …………………………………………………………………... (10)
L∞ =
a
…………………………………………………………….... (11)
1 b
to = t + 1
K
In
L  Lt
L
……………………………………………….. (12)
2. PLOT VON BERTALANFFY
Jika data tidak dikumpulkan dengan interval waktu yang sama.
Disebut juga Modal Progression Analysis.
Lt = L∞ ( 1 – ek(t-to) )
Lt
L
= 1 – e-k (t-to)
1  Lt
= e-k (t-to)
L
 Ln
1  Lt
L
= -kto + kt …………………………………………………………. (13)
Maka to =
y
a
b
a

b
3. PLOT GULLAND DAN HOLT
Untuk data panjang dengan interval waktu yang tidak sama. Asumsi bahwa laju
pertumbuhan dalam panjang (dL/dt) merupakan fungsi linier dari panjang (L).
dL
dT
= k ( L∞ - I ) …………………………………………………………(14)
dimana L∞ adalah nilai panjang untuk dL/dt = 0
L2 – L1
t 2 – t1
Y
= k L∞ - k I
a
bX
k = -b
L∞ = -a/b
Thank You
• ESTIMASI PERTUMBUHAN BERDASARKAN
DATA FREKWENSI PANJANG
Hasil perhitungan dengan metode Battacharya :
Kohort N1 : nilai rata-rata panjang 17,35 cm
simpangan baku 1,78 cm
Kohort N2 : nilai rata-rata panjang 27,77 cm
simpangan baku 2,66 cm
t2 – t1 = 0,5 tahun
Rumus : K 
1
L  Lt1 
ln
t 2  t1 L  Lt 2 
1
50  17.35
ln
 0.77
0.5 50  27.77
1 
Lt1  

t0  t1  ln 1 
K 
L 
1
 17.35 
 0.5 
ln 1 
  0.05
0.77 
50 

Model pertumbuha n Von Burtalanff y :
Lt  L1  exp  K t  t0 
Lt  501  exp  0.77t  0.05
 Estimasi ukuran rata - rata ikan berumur 1.5 tahun :
L1.5   501  exp  0.771.5  0.05
 34.8 cm