Bab 2 Medan Listrik Baru

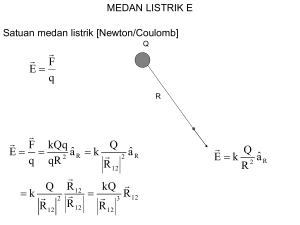
BAB 2 MEDAN LISTRIK
 PENGERTIAN MEDAN
 DEFINISI MEDAN LISTRIK
 GARIS-GARIS MEDAN LISTRIK
 MEDAN LISTRIK DARI MUATAN TITIK
 MEDAN LISTRIK DARI DIPOL LISTRIK
 MEDAN LISTRIK DARI MUATAN GARIS
 MEDAN LISTRIK DARI MUATAN BIDANG
 PENGERTIAN MEDAN
• Misalkan sebuah muatan titik q1 (positip) diletakkan di suatu tempat
di dalam ruang
• Bila terdapat muatan lain q2 (positip) di sekitarnya, maka muatan q1
memberikan suatu gaya tolak kepada muatan q2 yang besarnya dapat
tergantung pada besar kedua muatan dan jaraknya antar keduanya
• Pertanyaannya : bagaimana q1 mengetahui bahwa disekitarnya ada
muatan q2 ?
• Bagaimana menjelaskan fenomena ‘action at distance’ ini.?
• Fenomena ini dapat diterangkan dengan konsep/pengertian medan
dimana muatan q1 menghasilkan atau menyebarkan (set-up) suatu
medan di sekitarnya.
• Pada setiap titik P dalam ruang medan ini mempunyai besar dan arah.
• Besarnya tergantung pada besar q1 dan jarak titik P dari q1 sedangkan
arahnya tergantung dari posisi titik P terhadap q1.
• Medan skalar (temperatur, tekanan udara) = distribusi di dalam ruang
• Medan listrik = medan vektor
 DEFINISI MEDAN LISTRIK
• Misalkan di sekitar obyek bermuatan diletakkan suatu muatan uji qo
• Kemudian gaya yang bekerja padanya diukur, misalkan F
• Medan listrik didefinisikan sebagai :
F
E
qo
N
 C 
• Medan listrik = gaya Coulomb pada muatan sebesar 1 C
• Di ruang sekitar obyek bermuatan terdapat distribusi medan listrik
 GARIS-GARIS MEDAN LISTRIK
• Michael Faraday memperkenalkan konsep garis-garis medan listrik
• Dalam ruang di sekitar benda bermuatan digambarkan dipenuhi oleh
garis-garis gaya (lines of force).
• Arah medan listrik di suatu titik searah dengan garis singgung di
titik tersebut
• Besar medan listrik ditentukan oleh rapat garis gaya persatuan luas
 MEDAN LISTRIK DARI MUATAN TITIK

 F
E
q
Q
R

 F kQq
Q
E 
â R  k  2 â R
2
q qR
R 12

Q R 12
kQ 
 k  2    3 R 12
R 12 R 12
R 12

Q
E  k 2 â R
R
Contoh Soal 2.1
Dua buah muatan titik, + 8 q dan -2 q, dipegang tetap pada pada titik
A(0,0) dan B(L,0). Di titik mana medan listrik akibat kedua muatan ini
nol ?
Jawab :
Hanya mungkin di titik sebelah
kanan muatan negatip (yang lebih
kecil)
E1  E 2
k (8q )
k ( 2q )

2
x
( x  L) 2
( x  L) 2 2 1
 
2
x
8 4
xL 1

 2 x  2L  x
x
2
x  2L
x
Contoh Soal 2.2
Muatan Q1 berada di titik A(0,5) sedangkan muatan Q2 di titik B(12,0),
kedua muatan tersebut besarnya masing-masing adalah Q1 = 30 C dan
Q2 = - 10 C. Hitung medan listrik di titik C(2,-2)
A(0,5)
B(12,0)
C(2,-2)
Jawab :
A(0,5)
R31
B(12,0)
R32
C(2,-2)





R31  (2  0)i  (2  5) j  2i  7 j 

R31  2 2  7 2  7,28




kQ1 
9 x109 (30 x10 6 ) 
3
E31   3 R31 
(
2
i

7
j
)

(
1
,
399
i

4
,
898
j
)
x
10
N /C
3
7,28
R31





R32  (12  2)i  (0  (2)) j  10  2 j  R32  10 2  2 2  10,198




kQ2 
9 x109 (10 x10 6 ) 
3
E23   3 R32 
(
10
i

2
j
)

(
8
.
654
i

1
,
731
j
)
x
10
N /C
3
10,198
R32









3
3
E3  E31  E32  (1,399i  4,898 j ) x10  (8,654i  1,731 j ) x10  (10,053i  3,167 j ) x103 N / C
 MEDAN LISTRIK DARI MOMEN DIPOL LISTRIK p
1
q
1
q
E

2
2
4o 
4

d
d
o 
z 
z 
2
2


1
q
1
q


2
2
2
2
4o z 
d  4o z 
d 
1  
1  
 2z 
 2z 
2
2
q 
d 
d

 

1    1   
2 
4o z  2 z 
 2 z  
d
z  d 
 1 :
2z
q  d
  d

E
1




1



 

2 
4o z 
z
z
 

q
2d
1 qd
1 p



3
3
4o z
2o z
2o z 3
Contoh Soal 2.3
Sebuah molekul uap air menyebabkan medan listrik di sekitarnya. Bila
momen dipol listriknya adalah 6.2x10-30 Cm, hitung medan listrik yang
terjadi pada jarak z = 1.1 nm (z>> d = jarak antar muatan)
Jawab :
1 p
E
2o z 3
30
6
.
2
x
10
9
7 N
 18x10
 8.4x10
9 3
(1.1x10 )
m
 MEDAN LISTRIK DARI MUATAN GARIS
dq dianggap sebagai muatan titik yang menghasilkan medan
listrik sebesar :
1 dq
dE 
4o r 2
dq  dz r 2  z 2  d 2
dq
1
dz
dE 
4o z 2  d 2
r
z


d
dEsin 
dEcos 
Hanya ada komponen horisontal :
1
dz
d
dE cos  
4o z 2  d 2 z 2  d 2
1
d dz

4o (z 2  d 2 ) 3 / 2
dE

1
d dz
E 
2
2 3/ 2
4

(
z

d
)
o
z  
z      

2
z
 tg z  d tg  dz  d sec 2 d
d
z 2  d 2  d 2 tg 2  d 2  d 2 (tg 2  1)  d 2 sec 2 
( z 2  d 2 ) 3 / 2  d 2 sec 2  
dq
3/ 2
 d 3 sec 3 
r
z

d

dE
1
d dz
d
E 

2
2 3/ 2
4

(
z

d
)
4o
o
z  

2
d sec 2 d
  d 3 sec 3 
 
2
/ 2


cos d

4o d   / 2


/ 2

sin    / 2 
[1  (1)]
4o d
4o d

E
2o d
Contoh Soal 2.4
Sebuah batang tipis sepanjang L bermuatan sebesar q ditunjukkan pada
gambar di bawah ini. Buktikan bahwa medan listrik di titik P adalah :
q
1
E
2o y L2  4 y 2
Jawab :
dE
dE cos 
Medan listrik dari
muatan garis dengan
panjang terbatas
L
L
2
sin   2 
2
r
L
 
2

y
 
2
dE sin 


r
- L/2
L/2
dx




E
sin   
sin( )  sin( ) 
sin 
4o y
4o y
2o y
L
2

L


2o y  L  2
2o y
2
  y
2
L
2
1
 4y2

Contoh Soal 2.5
Sebuah batang plastik berbentuk busur lingkaran dengan sudut 120o dan
bermuatan – Q ditunjukkan pada gambar di bawah ini. Tentukan medan
listrik di titik P. Muatan tersebut terdistribusi merata sepanjang busur
lingkaran
Jawab :
ds  r d  dq  ds   rd
Medan listrik dE dalam arah y saling
menghilangkan :
1 rd
dE x  dE cos  
cos 
2
4o r
1 

cos d
4o r
60o
E

  60o
1 
cos d
4o r
1 
60

sin  60
2
4o r
1 
1.734 

2(0.867) 
4o r
4o r
1.734 
E
4o r
Q
0.477Q


2r
r
3
1.734  0.477Q 0.83Q
E

4o r
r
4o r 2
 MEDAN LISTRIK DARI MUATAN CINCIN
z
dq  ds cos   
r
1 dq
dE cos  
4o r 2
z
R 2  z2
z
R 2  z2
1
ds
z

4o R 2  z 2 R 2  z 2

1
z ds
4o ( R 2  z 2 ) 3 / 2
z
E   dE cos  
4o (R 2  z 2 ) 3 / 2
2 R
 ds
s 0
( 2R ) z
qz


2
2 3/ 2
4o (R  z )
4o ( R 2  z 2 ) 3 / 2
z  R
1 q
 E
4o z 2
 muatan titik
 MEDAN LISTRIK DARI MUATAN BIDANG
dE 
dq z

4o r  z
2
z 2

r  z2
4 o

z

4 o
 r

2 3/ 2

3 / 2
R
2
z


 2r dr z

4o r 2  z 2

3/ 2
2r dr
2 3 / 2
2r dr
dq   dA
r 0
u  r2  z2
 du  2rdr

1
2
z
z u

3 / 2
E
u du 


1
4 o
4 o 
2 o
2

 
z



1


2 o 
R 2  z2 

R   E 
2 o
  2r dr
z
r2  z2
R
0
Contoh Soal 2.6
Cakram (disk) pada gambar di bawah ini mempunyai jari-jari 2,5 cm dan
rapat muatan sebesar 5,3 µC/m2 pada permukaan atasnya.
a). Hitung medan listrik di sumbunya pada jarak 12 cm dari cakram tsb.
b). HItung medan listrik pada permukaan cakram
Jawab :
 
z 
a ). E 
1  2
2 
2o  z  R 
0.12


3 N
 18x109 (5.3x10 6 )1 

6
.
3
x
10

2
2
C
 0,12  0,025 

N
b). E 
 18x109 (5.3x10 6 )  3,0 x105
2 o
C
Contoh Soal 2.7
Dua buah plat yang luasnya masing-masing adalah A diletakkan
sejajar seperti pada gambar, dengan jarak antar plat adalah d. Muatan
sebesar –Q didistribusikan secara merata pada plat pertama sedangkan
muatan + Q didistribusikan pada plat kedua. Tentukan :
Tentukan medan listrik di setiap tempat.
-Q
I
+Q
II
(1)
III
(2)
Jawab :
-Q
E2
+Q
E2
E1
E1
E1
I
II
(1)
III
(2)


E I  E I1  E I 2 

0
2 o 2 o
E II  E II1  E II 2



Q


 
2 o 2 o
o
o A
E III  E III1  E III 2




0
2 o 2  o
E2
Ink-Jet Printing
• Drop generator mengeluarkan tetesan-tetesan (drops) tinta
• Drop charging unit memberikan muatan negatip) pada tetesan tinta
sesuai dengan besarnya input sinyal dari komputer
• Tetesan tinta yang masuk ke deflecting plate yang di dalamnya terdapat
medan listrik seragam E yang arahnya ke bawah
• Tetesan tinta akan mendapat gaya/percepatan ke atas dan menumbuk
kertas pada tempat yang diinginkan
• Untuk membentuk 1 hurup diperlukan kira-kira 100 tetesan tinta
Contoh Soal 2.8
Sebuah tetesan tinta bermassa 1,3x10-10 kg dan bermuatan sebesar
negatip 1,5x10-13 C masuk ke daerah diantara dua pelat dengan
kecepatan awal 18 m/s. Medan listrik diantara kedua pelat adalah 1,4x106
N/C dengan arah ke bawah dan panjang pelat adalah 1,6 cm. Hitung
defleksi vertikal pada saat keluar dari ujung pelat
Jawab :
ay 
F qE

m m
y
1
ayt 2
2
L
L  vxt  t 
vx
1 qE  L

y
2 m  vx
2

qEL2
 
2
2
mv

x
(1,5 x10 13 )(1,4 x10 6 )(1,6 x10  2 ) 2

2(1,3 x10 10 )(18) 2
 6,4 x10  4 m  0,64 mm
Contoh Soal 2.9
Dua buah pelat konduktor sejajar berjarak d = 2 cm yang bermuatan
negatip (sebelah atas) dan bermuatan positip (sebelah bawah)
menghasilkan medan listrik seragam di dalamnya sebesar 3000 N/C.
Sebuah elektron ditembakkan dari ujung kiri pelat positip dengan sudut
45o dengan kecepatan awal sebesar 6x106 m/s. Jika panjang pelat adalah
10 cm,
a) Apakah elektron tersebut akan menumbuk salah satu pelat ?
b) Bila ya, elektron tersebut menumbuk pelat yang mana dan dimana ?
L
-Q
E
Vo
d

+Q
F
m
s
6
o
6 m
Voy  Vo sin   6 x10 sin 45  4,242 x10
s
F  qE  (1,6 x10 19 )(3000)  4,8x10 16 N
Jawab :
Vox  Vo cos   6 x106 cos 45o  4,242 x10 6
F  ma
F 4,8x10 16
14 m
 a 
 5,275x10 2  9,8
31
m 9,1x10
s
L
E
Vo
d

F
0,1
8
Vox t  x  x o  0,1  t 

2
,
357
x
10
4,242 x106
1 2
Vo t  at  y  y o
2
1
y  (4,242 x10 6 )( 2,357 x10 8 )  (5,275x1014 )( 2,357 x10 8 )
2
 0,1  0,147  0,047
y negatip  menumbuk pelat bawah
L
E
Vo
d

F
Menumbuk pelat bawah  y = 0
2Vo 2(4,242x106 )
1 2
8
Vo t  at  0  t 


1
,
608
x
10
2
a
5,275x1014
x  Vox t  (4,242x106 )(1,608x10 8 )  0,0682m  6,82 cm
L
E
Vo
d

F
 DIPOL LISTRIK DI DALAM MEDAN LISTRIK
Suatu dipol listrik berada dalam medan listrik
Momen dipol listrik p membentuk sudut  dengan medan listrik E.
Kedua muatan mendapat gaya yang sama besar tetapi berlawanan arah
Dipol listrik akan mengalami torka (momen gaya) 
d
d
  F sin   F sin 
2
2
 Fd sin   pE sin 
  
  pE
Energi potensial rotasi :
U  W   d   pE sin d
 
 pE cos   p  E
Contoh Soal 2.10
Sebuah molekul uap air (H2O) mempunyai momen dipol listrik sebesar
6,2x10-30 Cm.
a). Berapa jarak antar pusat-pusat muatannya ?
b). Bila molekul tersebut ditempatkan dalam medan listrik sebesar
1,5x104 N/C, berapa momen gaya maksimum yang diterimanya ?
c). Berapa kerja yang harus dilakukan untuk memutarnya dari  = 0
sampai  = 180 o.
Jawab :
a ). p  qd  10ed  10(1,6x10 19 )d  6,2x10 30
6,2x10 30
12
d

3
,
9
x
10
m
19
10(1,6x10 )
b).   pE sin    maks  (6,2x10 30 )(1,5x10 4 ) sin 90o  9,3x10  20 Nm
c). W  U(0o )  U(180o )  pE cos(0o )  pE cos(180o )
 2pE  2(6,2x10 30 )(1,5x10 4 )  1,9x10  25 J
Soal Latihan 2.1
Dua buah muatan masing-masing sebesar + 20 C (sebelah kiri)
dan - 8 C (sebelah kanan) terletak pada satu garis lurus dengan
jarak 2 meter. Tentukan letak titik P dimana medan listriknya nol.
Jawab : 3,44 m
Soal Latihan 2.2
Dua buah muatan yang sama sebesar + q diletakkan pada kedua
sudut dari segitiga sama kaki yang bersisi d. Pada sudut puncak
yang besarnya 90o diletakkan muatan ketiga sebesar + 2q.
Tentukan besarnya medan listrik di titik P yang terletak di tengahtengah kedua muatan + q.
Jawab :
4 kq
d2
Soal Latihan 2.3
Dua buah pelat konduktor sejajar berjarak 2 cm sepanjang 10 cm
diberi muatan negatip (sebelah bawah) dan bermuatan positip
(sebelah atas) sehingga terdapat medan listrik seragam sebesar
2000 N/C. Sebuah proton
ditembakkan dari dari sebelah kiri
pelat bawah dengan kecepatan awal Vo pada sudut 30o terhadap
horisontal. Berapa kecepatan awal maksimum agar proton
tersebut tidak menumbuk pelat atas ? Proton : q=1,6x10-19C
m=1,67x10-27kg
Jawab : 0,184 x 106 m/s