Dinamika Dan Interaksi Soliton DNA Model Peyrard

1.3 Perumusan Masalah
Pada penelitian sebelumnya, telah
diperoleh solusi analitik untuk dinamika
DNA model PBD hingga orde ke-4.12 Lalu
ada penelitian ini akan ditinjau pemecahan
solusi numerik persamaan soliton DNA
model PBD dengan memberikan efek
gangguan menggunakan metode beda
hingga untuk dinamika DNA model PBD
hingga orde ke-3.
1.4 Hipotesis
Solusi numerik yang akan diperoleh
dari dinamika dan interaksi DNA model
PBD yang diberikan efek gangguan akan
menunjukkan hasil yang berbeda dengan
solusi eksak tanpa gangguan.
BAB 2
TINJAUAN PUSTAKA
2.1 Deoxyribose Nucleic Acid (DNA)
DNA atau Deoxyribo Nucleic Acid
merupakan substansi penurunan sifat yang
erat kaitannya dengan hampir semua
aktivitas biologi. DNA adalah asam
nukleotida, biasanya dalam bentuk heliks
ganda yang mengandung instruksi genetik
yang menentukan perkembangan biologis
dari seluruh bentuk kehidupan sel. DNA
berbentuk polimer panjang nukleotida,
mengkode barisan residu asam amino
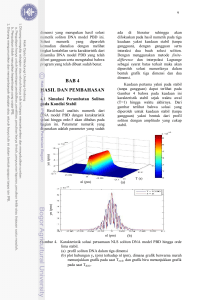
(a)
Gambar 1.
13
dalam protein dengan menggunakan kode
genetik, sebuah kode nukleotida triplet.13
DNA pada pengertian sempit adalah suatu
cetakan untuk membuat protein.14 DNA
membawa informasi genetik sel dan terdiri
dari ribuan gen. Setiap gen berfungsi
sebagai cetakan untuk membangun sebuah
molekul protein. Protein melakukan tugastugas penting untuk fungsi sel atau
berfungsi sebagai blok bangunan. Aliran
informasi dari gen ini menentukan
komposisi protein dan fungsi dari sel itu
sendiri.15
DNA
tersusun
sebagai
untai
komplementer dengan ikatan hidrogen di
antara mereka. Masing-masing untai DNA
adalah rantai kimia „batu bata penyusun‟,
yakni nukleotida, yang terdiri dari empat
tipe: Adenine (A), Cytosine (C), Guanine
(G) dan Thymine (T).13 DNA mengandung
informasi genetika yang diwariskan oleh
keturunan dari suatu organisme; informasi
ini ditentukan oleh barisan pasangan basa.
Sebuah untai DNA mengandung gen,
sebagai „cetak biru‟ organisme. Rantai
DNA memiliki lebar 22-24 Å, sementara
panjang satu unit nukleotida 3,3 Å.13
Struktur komplementer dan molekul DNA
ditunjukkan oleh Gambar 1.
Replikasi DNA adalah proses
penggandaan rantai ganda DNA. Proses
replikasi DNA ini ditunjukkan oleh
Gambar 2.
(b)
(a) Struktur untai komplementer DNA yang membentuk DNA beruntai
ganda.
(b) Struktur molekul DNA. Atom karbon berwarna hitam, oksigen merah,
nitrogen biru, fosfor hijau, dan hidrogen putih.
3
Replikasi DNA
DNA
Induk
Tahap 1
Pembukaan rantai
DNA
Tahap 2
Melengkapi pasangan
basa
Dua molekul DNA
semikonservatif
baru
Tahap 3
Pembentukan gula fosfat yang
menghubungkan nukleotidanukleotida pada dua rantai baru
Gambar 2. Proses Replikasi DNA.16
Satu pengamatan penting yang
menuntun Watson dan Crick ke penemuan
terkenal dari struktur heliks ganda DNA
adalah basa cenderung berpasangan
melalui ikatan hidrogen dan pasangan
yang terbentuk oleh purin dan pirimidin
memiliki ukuran yang hampir sama
sehingga pasangan-pasangan demikian
membentuk struktur dua rantai nukleotida
berikatan hidrogen yang sangat teratur.
Barisan pasangan basa dalam DNA
mengkode informasi untuk mensintesa
protein, adalah polimer yang terdiri dari
20 asam amino berbeda. Ikatan hidrogen
pada pasangan basa dalam DNA ini pada
suatu saat dapat mengalami pemutusan
yang disebut dengan proses denaturasi.
Selama replikasi DNA, yang terjadi
selama pembelahan sel, misalnya molekul
disalin dengan cara membukanya seperti
ritsleting.Transkripsi
DNA
adalah
pembacaan gen tunggal untuk mensintesa
protein.5
Pada sel, replikasi DNA terjadi
sebelum pembelahan sel. Sel prokariot
terus-menerus
melakukan
replikasi
DNA, sedangkan sel eukariot waktu
terjadinya replikasi DNA sangat teratur,
yaitu pada fase S daur sel, sebelum
mitosis atau meiosis I. Penggandaan
tersebut memanfaatkan enzim DNA
polimerase
yang
membantu
pembentukan ikatan antara nukleotidanukleotida
penyusun polimer DNA.
Proses replikasi DNA dapat pula
dilakukan in vitro dalam proses yang
disebut reaksi berantai polimerase (PCR).
Replikasi DNA dikatakan semikonservatif
jika masing-masing strand DNA berlaku
sebagai template untuk sintesa rantai baru,
dua molekul DNA baru akan dihasilkan,
masing-masing dengan satu rantai baru
dan satu rantai lama. Proses ini disebut
replikasi semikonservatif. 17
2.2 Solusi Soliton DNA Model PBD
Teraproksimasi
Untuk
mendeskripsikan
gerak
internal DNA dimulai dengan memilih
model aproksimasi yang bersesuaian.
Biasanya pilihan model bergantung pada
masalah yang ditinjau dan akurasi
deskripsi yang diperlukan.18 Dalam hal ini
untuk gejala denaturasi DNA digunakan
model PBD. Sedang untuk mempelajari
dinamika model nonlinier DNA model
PBD tersebut, diperlukan suatu algoritma
yang mencakup beberapa unsur, yaitu
memilih
gerakan
yang
dominan,
mengkonstruksikan persamaan diferensial
parsial terkait dan mencari solusi untuk
persamaan, serta menginterpretasikan
solusi yang diperoleh.8
Gejala denaturasi pada dinamika
DNA ditunjukkan oleh adanya solusi
soliton. Representasi grafis dari solusi
persamaan gerak yang memiliki solusi
soliton ditunjukkan oleh Gambar 3 yang
ditafsirkan sebagai keadaan peregangan
untai ganda DNA. Dalam dinamika
replikasi DNA, DNA diasumsikan
mengalami tiga gerakan, yaitu gerak
longitudinal (searah sumbu x), gerak
bending (searah sumbu y), dan gerak
memutar (torsional).
4
un
un-1
s1
m
k
yn (pm)
un+1
Morse
Potensial
k
s2
Bentuk B-DNA dalam model
Watson-Crick merupakan heliks ganda,
terdiri atas dua alur s1 dan s2 (Gambar 4)
yang dihubungkan oleh interaksi secara
harmonik dengan tetangga terdekat di
sepanjang rantai. Untai dipasangkan satu
sama lain oleh suatu ikatan hidrogen, yang
bersesuaian untuk perpindahan transversal
nukleotida.5
Berdasarkan Gambar 4, diasumsikan
bahwa massa nukleotida pada DNA
sebagai m dan kopling k konstan di
sepanjang untai yang sama.5 Struktur
helikoid dari untai DNA menunjukkan
bahwa nukleotida dari untai yang berbeda
menjadi
cukup
dekat,
sehingga
nukleotida-nukleotida
tersebut
dapat
berinteraksi melalui filamen air, artinya
bahwa nukleotida n salah satu rantai
berinteraksi dengan (n+h) dan (n-h)
nukleotida lainya. Nukleotida selanjutnya
mengalami perpindahan gerak transversal
un dan vn dari posisi kesetimbangannya di
4
sepanjang
arah
ikatan
hidrogen,
Hamiltonian
untuk
rantai
DNA
menjadi 9,10
𝑚
𝐻=
2
𝑢2 + 𝑣 2 +
𝑘
2
2
𝐷 𝑒 −𝑎
𝑢 𝑛 −𝑣𝑛
−1
2
Gambar 4. Representasi grafis model pegas
sederhana untuk rantai DNA.5
Dengan membuat transformasi ke
koordinat pusat massa yang mewakili
gerak tranversal ke dalam dan keluar,
maka akan lebih mudah menggambarkan
gerakan dua alur, yaitu
𝑥𝑛 =
𝑢 𝑛 +𝑣𝑛
, 𝑦𝑛 =
2
𝑢 𝑛 −𝑣𝑛
2
................ (2)
Bentuk Persamaan (1) setelah di
transformasi ke koordinat pusat massa
Persamaan (2) :
𝑚
𝐻 𝑥𝑛 =
2
𝐾
𝑥𝑛2 +
𝑘
2
2 𝑥𝑛 − 𝑥𝑛−1
2 −𝑥𝑛 + 𝑥𝑛+ℎ
2
2 −𝑥𝑛 + 𝑥𝑛−ℎ
𝑚
𝐻 𝑦𝑛 =
𝐾
2
2
𝑦𝑛2 +
𝑘
2
𝑦𝑛 + 𝑦𝑛+ℎ
𝐷 𝑒 −𝑎
2𝑦𝑛
2
2
............. (3)
−1
2
+ 𝑦𝑛 + 𝑦𝑛−ℎ
2
+
+
2 𝑦𝑛 − 𝑦𝑛−1
2
2
+
2
+
..................... (4)
dari hubungan Persamaan (3) dan (4) akan
diperoleh persamaan dinamika DNA yang
menggambarkan gelombang linear dan
non linear
𝑚𝑥𝑛 = 𝑘 𝑥𝑛+1 + 𝑥𝑛 −1 − 2𝑥𝑛 +
𝐾 𝑥𝑛 +ℎ + 𝑥𝑛−ℎ − 2𝑥𝑛
....... (5)
𝑢𝑛 −
𝑢𝑛−1 2 + 𝑣𝑛 − 𝑣𝑛−1 2 +
𝐾
𝑢𝑛 − 𝑣𝑛+ℎ 2 + 𝑢𝑛 − 𝑣𝑛−ℎ
vn+1
vn
vn-1
nl (pm)
Gambar 3. Solusi soliton pada DNA model
PBD
m
2
+
................... (1)
dimana k adalah konstanta harmonik
helicoid untuk untai yang sama; K adalah
konstanta harmonik helicoid untuk untai
yang berbeda; H adalah Hamiltonian
potensial morse yang mendekati potensial
ikatan hidrogen. D adalah kedalaman
potensial morse; dan a adalah jarak antar
nukleotida pada rantai yang berbeda.
dan
𝑚𝑦 = 𝑘 𝑦𝑛 +1 + 𝑦𝑛 −1 −2𝑦𝑛 −
𝐾 𝑦𝑛 +ℎ +𝑦𝑛 −ℎ + 2𝑦𝑛
2 2𝑎𝐷 𝑒 −𝑎 2𝑦𝑛 − 1 𝑒 −𝑎
2𝑦𝑛
(6)
Seperti dijelaskan dengan asumsi DNA
bergerak dengan amplitudo sangat kecil
dalam beberapa artikel dapat menerapkan
transformasi
𝑦 = 𝜀Φn atau Φ𝑛 =
𝑦𝑛
𝜺
; (𝜀 ≪ 1)...... (7)
5
Substitusi
Persamaan
(6)
ke
Persamaan (7) (yang artinya diasumsikan
bahwa osilasi nukleotida cukup besar
untuk anharmonik, tetapi masih cukup
kecil sehingga partikel berosilasi di sekitar
bagian bawah potensial Morse) menjadi
Φ𝑛 =
𝑘
𝑚
𝐾
𝑚
Φ𝑛+1 + Φ𝑛−1 −2Φ𝑛 −
Φ𝑛+ℎ + Φ𝑛−ℎ + 2Φ𝑛 −
𝜔𝑔2 (Φ𝑛
dimana: 𝜔𝑔2 =
2
2
,𝛼=−
3𝑎
3
+ 𝜀𝛼Φ𝑛 + 𝜀 𝛽Φ𝑛 ) ... (8)
4𝑎 2 𝐷
𝑚
2
,𝛽=
7𝑎 2
3
(9)
agar Persamaan (8) dapat dipecahkan,
harus diterapkan pendekatan semi-diskrit
yang artinya bahwa mencari solusi dalam
bentuk gelombang soliton DNA model
PBD.
Φ𝑛 𝑡 = 𝐹1 𝜀𝑛𝑙, 𝜀𝑡 𝑒 𝑖𝜃 𝑛 +
𝜀 𝐹0 𝜀𝑛𝑙, 𝜀𝑡
+ 𝐹2 𝜀𝑛𝑙, 𝜀𝑡 𝑒 𝑖2𝜃𝑛 𝑒 𝑖3𝜃𝑛
+𝑐. 𝑐 + 𝑂 𝜀 3 ................... (10)
Dari Persamaan (10) - (14) diperoleh
keadaan untuk semua persamaan dalam
Persamaan (8). Kasus kontinu dari
Persamaan (8) adalah menyamakan
koefisien untuk berbagai keadaan. Sebagai
contoh, dengan menyamakan koefisien
untuk 𝑒 𝑖𝜃 𝑛 kemudian diperoleh hubungan
dispersi
𝜔2 =
2𝑘
2𝐾
1 − cos 𝑞𝑙 +
cos 𝑞ℎ𝑙 +
𝑚
1+𝜔𝑔2 .................................... (15)
𝑚
Selanjutnya,
dengan
menurunkan
Persamaan (15) secara implisit terhadap q
𝜕𝜔
( ) maka akan diperoleh kecepatan grup
𝜕𝑞
𝑉𝑔 =
𝑙
𝑘 sin(𝑞𝑙) − 𝐾 sin(𝑞ℎ𝑙) ... (16)
𝜔𝑚
Dengan
cara
yang
sama
yaitu
menyamakan koefisien untuk 𝑒 𝑖0 = 1
yang artinya cos 𝑞𝑙 = cos 𝑞ℎ𝑙 = 1,
diperoleh
𝐹0 =
dengan 𝜃 ≡ 𝜃𝑛 = 𝑛𝑞𝑙 − 𝜔𝑡, .............. (11)
dimana l adalah jarak antara dua
nukleotida tetangga pada untai yang sama;
ω adalah frekuensi optik dari getaran
pendekatan linier; q adalah bilangan
gelombang soliton DNA; dan c.c adalah
istilah conjugate-complex dari fungsi F0.5
Untuk memecahkan Persamaan (10),
fungsi Fi akan ubah ke bentuk kontinu.
dengan mengambil batas 𝑛𝑙 → 𝑧 dan
menerapkan transformasi
𝑍 = 𝜀𝑧, 𝑇 = 𝜀𝑡 .............. (12)
sehingga
menghasilkan
kontinu berikut
pendekatan
−2𝛼
𝐹1
4𝐾
2
𝑚𝜔𝑔
1+
dengan 𝜇 = −2𝛼 1 +
4𝐾
2
.......... (17)
−1
𝑚 𝜔 𝑔2
maka diperoleh hubungan
𝐹0 = 𝜇 𝐹1
Asumsikan 𝑒
𝐹2 =
𝑖2𝜃𝑛
2
............... (18)
untuk koefisien 𝐹2
𝜔 𝑔2 𝛼
2𝑘
𝑚
cos 2𝑞𝑙 −1
2𝐾
−
𝑚
cos 2𝑞ℎ𝑙 +1 +4𝜔 2
𝐹12
............................................................ (19)
dengan
𝛿 =
𝜔 𝑔2 𝛼
2𝑘
𝑚
2𝐾
𝑚
cos 2𝑞𝑙 −1 −
cos 2𝑞ℎ𝑙 +1 +4𝜔 2
𝐹 𝜀 𝑛 ± ℎ 𝑙 → 𝐹 𝑍, 𝑇 ± 𝐹𝑍 𝑍, 𝑇 𝜀𝑙ℎ +
1
𝐹𝑍𝑍 (𝑍, 𝑇)𝜀 2 𝑙 2 ℎ2 ... (13)
hubungannya menjadi
dimana FZ dan FZZ berarti turunan
5
terhadap Z. Hal ini memungkinkan untuk
mendapatkan ekspresi baru untuk fungsi
Φ𝑛 (𝑡) :
Fungsi F0 dan F2 kemudian dapat
dinyatakan ke dalam bentuk fungsi F1
dengan
menggunakan
transformasi
koordinat yang baru lagi
Φ𝑛 𝑡 = 𝐹1 𝑍, 𝑇 𝑒 𝑖𝜃 𝑛 + 𝜀 𝐹0 𝑍, 𝑇 +
𝐹2 𝑍, 𝑇 𝑒 𝑖2𝜃𝑛 + 𝑐. 𝑐
= 𝐹1 𝑒 𝑖𝜃 𝑛 + 𝜀 𝐹0 + 𝐹2 𝑒 𝑖2𝜃𝑛 +
𝐹1∗ 𝑒 −𝑖𝜃 𝑛 + 𝜀𝐹2∗ 𝑒 −𝑖2𝜃𝑛 .......... (14)
𝑆 = 𝑍 − 𝑉𝑔 𝑇 atau 𝑍 = 𝑉𝑔 𝑇 + 𝑆, 𝜏 = 𝜀𝑇
............................................................ (21)
2
𝐹2 = 𝛿𝐹1 2 ................. (20)
Untuk koefisien 𝑒 𝑖𝜃 𝑛 kasus kontinu
6
𝜀 2 𝐹1𝑇𝑇 − 2𝑖𝜔𝜀𝐹1𝑇 − 𝜔2 𝐹1 =
𝑘
{2𝐹1 cos 𝑞𝑙 − 1 + 2𝑖𝜀𝑙𝐹1𝑍 sin 𝑞𝑙 +
𝐾
𝜀 2 𝑙 2 𝐹1𝑍𝑍 cos 𝑞𝑙 }𝑒 𝑖𝜃 𝑛 − {2𝐹1 cos 𝑞ℎ𝑙 + 1 +
𝑚
2𝑖𝜀𝑙ℎ 𝐹1𝑍 sin 𝑞ℎ𝑙 + 𝜀 2 𝑙 2 ℎ2 𝐹1𝑍𝑍 cos(𝑞ℎ𝑙)}𝑒 𝑖𝜃𝑛 −
𝜔𝑔2 𝐹1 + 𝜀 2 2𝛼 𝜇 + 𝛿 + 3𝛽 𝐹1 1 𝐹1 𝑒 𝑖𝜃 𝑛 ................ (22)
𝑚
Berdasarkan Persamaan (22)
persamaan NLS dapat ditulis
𝑖𝐹1𝜏 +
𝑙2
1
maka
1 𝑑
𝑘 cos 𝑞𝑙 − 𝐾 ℎ2 cos(𝑞ℎ𝑙) −
2𝜔 𝑚
𝑙2
2𝜔 𝑚
𝑉𝑔2
.......... (25)
2𝜔
𝑑𝑢 2
𝑑𝑆
𝑖𝐹1𝜏 + 𝑃𝐹1𝑆𝑆 + 𝑄 𝐹1 2 𝐹1 = 0 ............ (26)
−𝜎𝑢 + 𝑃
𝜕𝑆 2
Misalkan
𝑑𝑠
+𝑃
𝑑 2 𝑢 𝑑𝑢
......... (27)
𝑑𝑆 2 𝑑𝑠
𝑑𝑠
𝑄
𝑑𝑆
=
2𝑃/𝑄
2𝜎
𝑢=
𝑄
......... (32b)
dan
𝑠𝑖𝑛 𝜓
𝑐𝑜𝑠 𝜓 𝑑𝜓 , maka ruas kanan
𝑑𝑢
𝑢
2𝜎
−𝑢 2
𝑄
𝑑𝜓
→
2𝜎
𝑄
......... (33)
𝑠𝑖𝑛 𝜓
Integrasikan ruas kanan Persamaan (33)
terhadap variable ψ, diperoleh
+ 𝑄𝑢 = 0 ..... (28)
𝑑𝑢
2
Persamaan (32b) dalam variable ψ dapat
ditulis menjadi
3
+ 𝑄𝑢3
2𝜎
𝑑𝑢 =
𝑑𝜓
2𝜎
𝑄
𝑑𝑠
𝑑𝑢
𝑄
𝜎𝑢2 − 𝑢4 ... (32a)
2𝜎
−𝑢 2
𝑄
𝑢
Selanjutnya Persamaan (28) dikali dengan
𝑑𝑢
, diperoleh
−𝜎𝑢
1
𝑃
𝑑𝑢
dengan σ merupakan frekuensi gelombang
soliton DNA yang berperan sebagai
variabel bebas dan 𝑢(𝑆) merupakan fungsi
real.
Kemudian
Persamaan
(27)
disubstitusikan ke Persamaan (26)
𝜕2𝑢
=
atau
Untuk menyelesaikan Persamaan (26)
harus menggunakan ansatz (tebakan),
sehingga dapat diperoleh solusi eksak
soliton DNA. Persamaan ansatz dari
persamaan NLS tersebut diberikan
𝐹1 𝑆, 𝜏 = 𝑢(𝑆)𝑒
2
Dari hasil ini dapat ditulis kembali
Persamaan (31) menjadi
Maka persamaan NLS pada Persamaan
(23) dapat ditulis menjadi5
𝑖𝜎𝜏
𝑄
+ 𝑢4 = 𝑐 ... (31)
𝑑𝑆
dimana c merupakan sebuah konstanta.
Selanjutnya kembali akan diberikan
batasan pada solusi yang memiliki kondisi
𝑑𝑢
→ 0 dan u → 0 pada S → ± ∞ dan
𝑑𝑆
mengimplikasikan c = 0.
𝑘 cos 𝑞𝑙 − 𝐾 ℎ2 cos(𝑞ℎ𝑙) −
.............................................
(24) 𝜔 2
𝑔
𝑄=−
2𝛼 𝜇 + 𝛿 + 3𝛽
2
𝑑𝑢 2
−𝜎𝑢2 + 𝑃
............................................................ (23)
dengan koefisien dispersi
1
𝑄
+ 𝑢4 = 0 ... (30)
𝑑𝑆
yang mengindikasikan bahwa
𝑉𝑔2𝐹1𝑆𝑆−𝜔𝑔22𝜔2𝛼𝜇+𝛿+3𝛽𝐹11𝐹1=0
𝑃=
𝑑𝑢 2
−𝜎𝑢2 + 𝑃
2 𝑑𝑆
𝑠𝑖𝑛 𝜓
=
1
2𝜎
𝑄
𝑙𝑛
1
𝑠𝑖𝑛𝜓
−
𝑐𝑜𝑠 𝜓
𝑠𝑖𝑛 𝜓
Ruas kanan Persamaan (34)
variabel u dapat dinyatakan
= 0 ...... (29)
..... (34)
dalam
Persamaan (29) dapat dituliskan kembali
dalam bentuk
1
2𝜎
𝑄
𝑙𝑛
1
𝑠𝑖𝑛𝜓
−
𝑐𝑜𝑠 𝜓
𝑠𝑖𝑛 𝜓
=
1
2𝜎
𝑄
𝑙𝑛
2𝜎
𝑄
𝑢 2𝑄
2𝜎
1− 1−
𝑢
........................ (35)