Slide 1 - WordPress.com

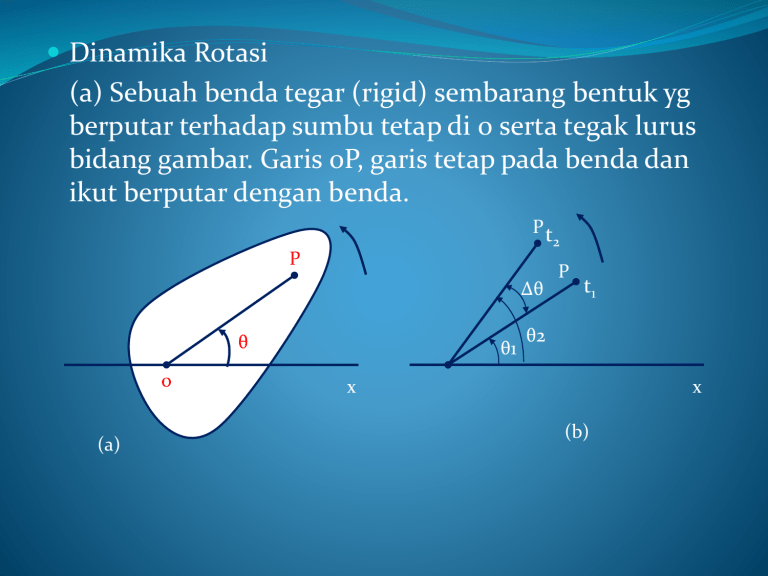
 Dinamika Rotasi
(a) Sebuah benda tegar (rigid) sembarang bentuk yg
berputar terhadap sumbu tetap di 0 serta tegak lurus
bidang gambar. Garis 0P, garis tetap pada benda dan
ikut berputar dengan benda.
Pt
P
Δθ
θ
0
(a)
θ1
2
P
t1
θ2
x
x
(b)
(b) Perubahan sudut Δθ suatu benda berputar

 Kecepatan sudut rata-rata  :

(rad / s )
t
 Kecepatan sudut sesaat (ω):
 d

t 0 t
dt
  lim
 Percepatan sudut rata-rata  :

 
t
 Percepatan sudut sesaat (α):
 d d d d 2
  lim


 2
t 0 t
dt dt dt
dt
d d
d

 .
d dt
d
(rad / s 2 )
 Rotasi dengan percepatan sudut konstan :
   0  t
  0 t  12  t 2
 2  02  2
 Hubungan Kecepatan Sudut dan Kecepatan Linier
dengan Percepatan
Jika θ dalam radian : S = r θ
didiferensiasi terhadap waktu :
V
P
r
s
θ
x
ds
d
r
dt
dt
V  r  (5.1)
 Dengan mendiferensiasi pers. 5.1 terhadap waktu :
dV
d
r
dt
dt
aT  r 
aT = r α
a
Komponen radial percepatan
di titik P :
P
aR = ω2 r
V2
aR 
  2 r  V
r
r
θ
0
x
 Gaya Putar dan Percepatan Sudut
Dinamika rotasi terhadap sumbu tetap yaitu relasi
antara gaya-gaya terhadap suatu benda yang berputar
dan percepatan sudutnya.
Fi
θi
mi
fi
φi
ri
0
Sebuah benda tegar yg berputar terhadap
sebuah sumbu tetap melalui titik 0 yang
tegak lurus bidang gambar.
merupakan salah satu partikel benda yg
massanya mi. Partikel itu mengalami gaya
luar Fi dan juga gaya dakhil fi , yaitu resultan
gaya-gaya yg dilakukan terhadapnya oleh
semua partikel lain benda itu.
Tinjau gaya Fi dan fi yg terletak pada bidang
yg tegak lurus pada sumbu. Dari hukum
Newton II :
Fi + fi = mi ai
 Diuraikan ke komponen radial dan komponen
singgung. Maka:
Fi cos i  f i cos i  mi aiR  mi ri 2
Fi sin i  f i sin i  mi aiT  mi ri
 Apabila kedua ruas persamaan kedua dikalikan
dengan jarak ri dari partikel ke sumbu, diperoleh:
Fi ri sin  i  f i ri sin   mi ri 2 (5.2)
 Suku pertama di ruas kiri adalah momen Гi gaya luar
terhadap sumbu dan suku kedua ialah momen gaya
dakhil. Apabila persamaan (5.2) dijumlahkan maka
momen-momen gaya dakhil akan saling meniadakan ,
karena momen resultan setiap pasangan aksi-reaksi
sama dengan nol. Sehingga:
   i   Fi ri sin i
 Karena benda itu tegar,maka semua partikel memiliki
percepatan sudut α yg sama dan oleh karena itu:
  (m1r12  m2r22  ....)  ( mi ri2 ) (5.3)
 Jumlah Σmiri2 disebut momen kelembaman benda
terhadap sumbu yg melalui titik O dan dilambangkan
dengan I :
2
I   mi ri
 Maka persamaan 5.3 menjadi :
d
  I  I
dt
Artinya apabila seuah benda tegar diputar terhadap suatu
sumbu tetap, maka resultan gaya putar (Torsi) luar
terhadap sumbu itu sama dengan hasil kali momen
kelembaman benda itu terhadap sumbu dengan
percepatan sudut.
 Sebuah roda berjari-jari
R massa m2 dan momen
kelembaman I terpasang
pada sebuah poros yg
bertopang pd gandar yg
tidak bergerak. Seutas
tali lemas dan ringan
dililitkan keliling roda
itu. Pada tali ini
bergantung sebuah
benda bermassa m1.
Gesekan di dalam
gandar(bearing)
diabaikan. Tentukan
percepatan benda
tergantung.
 Gambar
P
R

w2
T
T

w1
m1
 Solusi:
Gaya resultan benda yg tergantung w1 – T, dari Hukum
Newton II:
w1 – T = m1 a (1)
 Gaya P dan w2 tidak punya momen terhadap sumbu roda.
Gaya putar resultan pada roda terhadap sumbu ialah TR,
dan berdasarkan hukum Newton II untuk rotasi:
TR = Rα
(2)
 Karena percepatan linier benda yg tergantung sama dengan
percepatan singgung tepi roda, maka:
a=Rα
(3)
 Penyelesaian sekaligus persamaan 1, 2,3 diatas :
1
a  g.
1  ( I / m1 R 2 )
 Menghitung Momen Inersia (I)
B
10 g
5 cm
A
30 g
4 cm
3 cm
Hitung momen Inersia:
a. Terhadap sumbu melalui A tegak lurus
bidang gambar
b. Terhadap sumbu yg berhimpitan dengan
batang BC
C
20 g
 Solusi:
a. I = Σmiri2 = 10 x 52 + 20x 42 = 570 g cm2
b.I = Σmiri2 = 30 x 42 = 480 g cm2
 Untuk suatu benda yg bukan terdiri atas massa titik
melainkan atas materi yg terdistribusi secara tidak
terputus-putus maka:
I  lim
m0
2
2
r

m

r

 dm
 Jika dV ialah volume dan dm adalah massa sebuah
elemen, maka kerapatan (rapat massa) ρ didefinisikan
berdasarkan hubungan: dm = ρ dV , sehingga:
I   r 2  dV
 Kalau rapat massa sebuah benda sama di semua titik,
maka benda itu dikatakan uniform, maka:
I    r 2 dV
 Momen Inersia dari beberapa bentuk sederhana dan
homogen
A. Batang Langsing
y
l
L l
I
l
L-l
L l
dm
0
x
2
x
  dx
dx
L
Dengan memasukkan dm = λ dx dengan
λ adalah massa persatuan panjang =m/L
dan batas integrasi dari x = -1 samapai x
= L – l diperoleh :
1 3
 x
3
l


1
  ( L  l )3  (l )3
3
1
  ( L3  3L2l  3Ll 2 )
3
1m 3
I
( L  3L2l  3Ll 2 )
3L
1
I  m( L2  3Ll  3l 2 ) (5.4)
3
 Piringan Tipis
dr
I   r 2 dm
R
r
0
dm = δ dA
dA = 2π r dr
  r 2 2r dr
R
0
R
  r 3 2 dr
0
Piringan tipis berjari-jari R
mempunyai massa persatuan luas = δ
= m/A. Piringan diputar dengan
sumbu putar pada titik 0 tegak lurus
bidang gambar
2 R 4  mR 4
I

4
2A
karena A  R 2 , maka :
I  12 mR 2
 Silinder Berongga Konsentris
dm = ρ dV
= ρ .2π r dr. L
dr
I   r 2 dm
  r 2  .2r dr L
r
R2
I  2L   r 3 dr
R1
L
Bila benda homogen , ρ sama disetiap titik:
R2
I  2 L  r dr 
3
R1
L
2
R
4
2
 R14

I  12 m( R12  R22 )  m  L( R22  R12 )
untuk silinder pejal R1  0 dan R2  R
R1
R2
I  12 mR 2
untuk silinder tipis R1  R2  R
I  mR 2
 Gerak Menggelinding
merupakan gerak campuran yaitu gerakan translasi
pusat massa dan gerak rotasi.
ω
Q
O
ωR
P
Vo
Vo
Suatu silinder menggelinding dengan
jari-jari R dan massa M. Titik-titik P, O,
dan Q masing-masing adalah titik-titik
dasar yaitu titik singgung antara tanah
dengan silinder, pusat massa dan
puncak silinder.
Kecepatan pusat massa O adalah Vo,
ini sama dengan V T = ω R jadi Vo = ωR
 Energi kinetik yg dipunyai oleh silinder yang
menggelinding adalah:
Ek  12 MVo2  12 I 2
 Untuk silinder menggelinding pada bidang miring
R
I
S
Pada kedudukan I energi yang
dipunyai adalah energi
potensial :
Ep = M g (h + R)atau
Ep = M.g (h + R cos θ )
θ
h
II
θ
 Berdasarkan hukum kekekalan Energi:
Mg (h  R)  12 MV 2  12 I 2  MgR
 Dengan memasukkan I = ½ MR2 dan V = ωR, maka:
V 
Mgh  12 MV  12 ( 12 MR ) 
R
 34 MV 2
2
V
4
3
gh
2
2
Terlihat bahwa kecepatan benda
menggelinding lebih kecil dari pd benda
meluncur tanpa gesekan yg
kecepatannya:
V  2 gh
 Energi Kinetik, Usaha dan Daya
Bila sebuah benda tegar berputar terhadap suatu
sumbu tetap, kecepatan Vi sebuah partikel pada jarak
tegak lurus ri dari sumbu itu sama dengan riω ,
dimana ω adalah kecepatan sudut. Maka energi
kinetik partikel itu adalah:
1
2
miVi 2  12 mi ri 2 2
dan energi kinetik total benda itu :
Ek   12 mi ri 2 2 
1
2
 m r 
2
2
i i
I   mi ri 2  momen kelembaman, sehingga :
Ek  12 I 2
 Contoh: gaya luar F dilakukan di titik P sebuah benda tegar yg berputar
terhadap sumu tetap melalui O , tegak lurus bidang gambar. Ketika
benda itu berputar melalui sudut kecil dθ titik P bergerak sejauh ds = r
dθ dan usaha yg dilakukan oleh gaya F ialah:
W   Fs ds   Fs r d
F
Fs
karena Fs r ialah momen gaya 
terhadap sumbu, maka :
2
W    d
φ
1
  I  I
ds
dθ
O
P
d
d
d  I d
2
2
1
1
W    d   I d  12 I22  12 I12
Artinya usaha momen rsultan sama dengan
pertambahan energi kinetik
 Jika V kecepatan titik tangkapnya, maka daya yg
ditimbulkan oleh gaya Г adalah:
P  Fs V  Fs r 
P   ana log dengan P  Fs V
 Contoh : sebuah pabrik mobil membuat ketentuan
bahwa mesinnya memberikan 345 Hp dan gaya putar
475 Lb ft. Berapa kecepatan sudut yg bersesuaian ?
solusi:
P 345 x 550
 
 400 rad / s

475
 Momentum Sudut
d d ( I )
  I    I

dt
dt
L  I  momentum sudut
 Sehingga:
dL

dt
atau gaya putar resultan sama dengan kecepatan
perubahan momentum sudut, tepat seperti gaya luar
resultan sama dengan kecepatan perubahan momentum
linier.
kalikan dengan dt dan integrasikan, didapat:
t
 dt 
L  L0
0


Im puls sudut gaya putar
Jadi Impuls sudut resultan gaya putar pada suatu benda
sama dengan perubahan momentum sudut benda.
 Contoh soal: sebuah roda yg diameternya 3 m
mempunyai kecepatan sudut /angular yg berkurang
secara uniform dari 100 rpm pada t = 0 hingga
berhenti pada t = 4 detik
hitung :
a. Percepatan tangensial
b. Percepatan normal sebuah titik di tepi roda pada
t = 2 detik
 Solusi:
kecepatan awal :
0  100 rpm 
2 .100
 10,47 rad / det
60
 Setelah 4 detik ωt = 0
karena berkurang secara uniform, maka α konstan
sehingga:      t
t
0
0  10,47   .4
 
10,47
 2,62 rad / s 2
4
 Percepatan tangensial: aT = R α =1,5 x 2,62 = 3,93 m/s2 .
 Percepatan Normal
Pada t = 2 detik
ω2= 10,47 – 2,62 x 2 = 5,23 rad/s
V2 = R . ω2= 1,5 x 5,23 = 7,85 m/s
maka:
V 2 7,852
aR 
R

1,5
 41,08 m / s 2
 Sebuah roda gila memerlukan waktu 3 detik untuk
berputar melalui 234 rad. Pada akhir waktu ini
kecepatan sudutnya 108 rad/s.
Hitung: Percepatan sudut konstannya
 Solusi:
2
1
  0 t  2  t
234  0 .3  12  32
234  4,5
0 
 78  1,5
3
t   0   t
108  (78  1,5 )   .3
108  78  1,5
108  78

 20 rad / s 2
1,5
 Tentukan momen kelembaman sebuah batang yg
diameternya 4 cm dan panjangnya 2 m, massanya 8 kg.
a. Terhadap suatu sumbu yg tegak lurus pada batang
dan lewat salah satu ujungnya
b. Terhadap sumbu memanjang melalui pusat batang
itu
 Solusi:
a.
d
l=0
L
1
I  m( L2  3Ll  3l 2 )
3
1
 m L2
3
1
I  .8.2 2  10,67 kg.m 2
3
b. Silinder pejal
I  12 m R 2
 12 .8.0,02 2
I  0,0016 kg.m 2
 Hitung percepatan linier balok A dan B dan tegangan
dalam tiap bagian tali massa balok A = 8 gr , B = 4 gr dan
radius roda = 0,5 m. jika tidak ada gesekan pd permukaan
roda itu. Momen kelembaman roda terhadap sumbu 0,125
kg.m2
 R
B
A