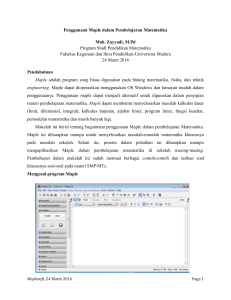
bab ii operasi dasar maple

BAB II OPERASI DASAR MAPLE
7
_____________________________________________________________________
BAB II
OPERASI DASAR MAPLE
2.1. Fungsi
Maple mempunyai library fungsi yang sangat besar. Secara sintak, fungsi
adalah tipe ekspresi. Fungsi-fungsi mempunyai nama dengan nol atau beberapa
argumen, dan mereka menghasilkan suatu nilai sebagai hasil pemanggilan fungsi.
Sebagai contoh:
> a := -5;
a := -5
> abs(a);
5
> a;
-5
Hasil perhitungan nilai mutlak ”a” diberikan sebagai akibat pemangilan fungsi
abs(a). Variabel a sendiri tidak berubah. Jika diinginkan untuk merubah nilai
variabel, gunakan:
> a := abs(a);
a := 5
Berikut ini adalah beberapa fungsi matematika umum :
Fungsi
Keterangan
abs(x)
Harga mutlak atau besarnya biangan kompleks
arccos(x)
Invers Cosinus
ceil(x)
Pembulatan ke arah plus tak hingga
conjugate(x)
Konjugat bilangan kompleks
cos(x)
Cosinus
exp(x)
Pangkat dengan bilangan pokok e
Im(x)
Bagian imaginer dari bilangan kompleks
lcm(x,y)
Kelipatan
persekutuan
terkecil
(KPK)
dari
bilangan bulat x dan y
log(x)
Logaritma natural
sign(x)
Memberikan tanda dari argumen, sign(-0.1) = -1
sqrt(x)
Akar kuadrat
Fungsi lain yang berkaitan/sejenis dapat dilihat pada menu Help.
_____________________________________________________________________
Program Studi Matematika
Jurusan Matematika FMIPA Universitas Brawijaya
BAB II OPERASI DASAR MAPLE
8
_____________________________________________________________________
Latihan:
Cobalah fungsi-fungsi di atas termasuk fungsi-fungsi lain yang sejenis.
2.2. Tipe Dasar dan Konversi
Maple mempunyai sejumlah tipe obyek. Tipe dari nilai numerik di antaranya
adalah integer, float (floating-point atau pseudo-real), fraction, rational, dan boolean.
Beberapa tipe obyek yang lebih kompleks misalnya string, polinom, series, matrix,
vector, set, dan procedure.
Integer diekspresikan seperti string yang terdiri dari satu atau beberapa digit dengan
tanda; seperti ”-9” atau ”2341”. Bilangan Rational adalah rasio antara dua bilangan
integer; seperti ”1/4” atau ”-3/7” dan akan disederhanakan oleh Maple:
> -3/24;
-1/8
Bilangan Floating point memuat titik desimal secara eksplisit; setiap integer atau
ekspresi rasional yang memuat titik desimal akan dievaluasi sebagai floating point:
> 2/3;
2/3
> 2./3.;
0.6666666667
Maple mempunyai variabel global yang disebut ”Digits” yang dapat digunakan untuk
mengkontrol akurasi operasi floating point. Default Digits adalah 10 tetapi dapat
diubah dengan menugaskannya dengan bilangan lain:
> Digits:=4;
Digits := 4
> 1.0/3.0;
.3333
> Digits:=10;
Digits := 10
> 1.0/2.0
.5000000000
Konversi dari suatu tipe data ke tipe data lainnya juga dapat dilakukan oleh Maple.
Sebagai contoh:
> convert(2/3,float);
.6666666667
_____________________________________________________________________
Program Studi Matematika
Jurusan Matematika FMIPA Universitas Brawijaya
BAB II OPERASI DASAR MAPLE
9
_____________________________________________________________________
Cara lainnya adalah dengan menggunakan fungsi evalf.
> evalf(2/3);
.6666666667
> evalf(2/3,5);
.66667
Beberapa kegunaan perintah Convert adalah
> convert(9, binary);
1001
> convert( [1,2,3,4], `+` );
10
> f := seq( x[i]^i, i=1..4 );
2
3
f := x1, x2 , x3 , x4
4
> convert([f], `*`);
2
3
x1 x2 x3 x4
4
> convert( 1.23456, fraction );
3858
3125
> f := (x^3+x)/(x^2-1);
f :=
x3x
x21
> convert(f, parfrac, x);
x
1
1

x1 x1
> s := series(f,x,4);
s := x2 x3O( x5 )
> convert(s, polynom); # Buang bentuk order
x2 x3
_____________________________________________________________________
Program Studi Matematika
Jurusan Matematika FMIPA Universitas Brawijaya
BAB II OPERASI DASAR MAPLE
10
_____________________________________________________________________
> f := sinh(x)+sin(x);
f := sinh( x )sin( x )
> convert(f, exp);
1 x 1 1 1  (x I)
1
e  x  I  e  ( x I ) 

2
2e
2 
e


Laihan: Pelajari command eval dan convert pada menu Help.
2.3. Package dan Libraries
Package
dalam Maple adalah kumpulan beberapa fungsi yang saling
berkaitan; Library adalah kumpulan dari beberapa package. Salah satu contoh
package adalah linalg, yaitu paket tentang aljabar linear. Untuk menggunakan
package, paket tersebut harus terlebih dahulu dipanggil dengan perintah with:
> with(linalg):
Warning, the protected names norm and trace have been redefined and
unprotected
(Jika perintah di atas diakhir dengan semicolon, Maple akan menunjukkan
sekumpulan fungsi yang ada di paket aljabar linear. Ketika Maple memanggil suatu
paket, Maple akan mengecek apakah suatu fugsi baru telah mengganti fungsi yang
sudah ada. Jika ya, maka Maple akan memberikan peringatan. Contohnya, karena
linalg mempunyai fungsi untuk menghitung trace suatu matriks, yang disebut trace,
tetapi trace juga merupakan fungsi untuk debugging; maka suatu peringatan akan
diberikan. Fungsi yang baru (yang ada di paket) siap digunakan tetapi fungsi yang
lama dengan nama yang sama tidak dapat diakses lagi. Untuk mengembalikan kondisi
semula, gunakan perintah restart, tetapi perintah ini akan menghapus seluruh
memori/variabel yang ada di worksheet.
2.4. Penyederhanaan
Hampir seluruh ekspresi yang dihasilkan Maple sesuai dengan input yang
diberikan. Tetapi untuk beberapa kasus sederhana, Maple secara otomatis melakukan
penyederhanaan ekspresi, misalnya 0*2 akan diubah secara langsung oleh Maple
menjadi 0. Maple tidak menyederhanakan sebagian ekspresi karena dua alasan:

Biaya: pemfaktoran suatu ekspresi memerlukan waktu yang cukup lama.

Perbedaan arti ’sederhana’: Suatu ekspresi yang sederhana bagi seorang
pengguna mungkin tidak sederhana bagi pengguna yang lain.
_____________________________________________________________________
Program Studi Matematika
Jurusan Matematika FMIPA Universitas Brawijaya
BAB II OPERASI DASAR MAPLE
11
_____________________________________________________________________
Untuk menyederhanakan ekspresi dapat digunakan perintah simplify:
> 4^(1/2) +3;
4 3
> simplify(%);
5
> simplify(% + sin(x)^2 + cos(x)^2,trig);
6
Perintah expand digunakan untuk menguraikan perkalian atas penjumlahan:
> c:=(x+y)*(x-y);
c := ( xy ) ( xy )
> expand(c);
x2y2
Perhatikan bahwa bentuk x^2+y*x-x*y-y^2 telah disederhanakan menjadi x^2-y^2.
Untuk mengetahui lebih banyak tentang penyederhanaan, lihat ?simplify, ?expand
dan ?factor.
2.5. Penjumlahan (Summation)
Penjumlahan (dalam notasi  ) di Maple dapat dilakukan baik untuk
jumlahan tentu maupun tak tentu (secara simbolik), yaitu dengan menggunakan
perintah sum. Dalam hal ini, indeks jumlahan harus merupakan variabel
matematika. Contoh:
> x; # untuk meyakinkan bahwa x adalah variabel matematika
x
> sum(x^i,i);
# jumlahan tak tentu
xi
x1
> sum(x^i,i=1..5); sum(i,i=0..10);
xx2x3x4x5
55
2.6. Menyelesaikan (Sistem) Persamaan
Maple mempunyai banyak fungsi untuk menyelesaikan berbagai (sistem)
persamaan. Yang paling sederhana dan paling sering digunakan adalah solve.
> solve( f=m*a, a );
f
m
_____________________________________________________________________
Program Studi Matematika
Jurusan Matematika FMIPA Universitas Brawijaya
BAB II OPERASI DASAR MAPLE
12
_____________________________________________________________________
> solve( {f=m*a}, {a} );
{ a
f
}
m
> eq := x^4-5*x^2+6*x=2;
eq := x45 x26 x2
> solve(eq,x);
1, 1, 3 1, 1 3
> sols := [solve(eq,x)];
sols := [ 1, 1, 3 1, 1 3 ]
> sols[1];
1
Catatan: Periksa ?solve.
2.7. Penugasan dan Substitusi
Fungsi assign digunakan untuk mengambil penyelesaian yang dihasilkan oleh
solve. Untuk menlihat hal ini, perhatikan contoh berikut:
> # x dan y adalah variable matematika
> x,y;
x, y
> sols:=solve({x+2*y=3,y+1/x=1},{x,y});
1
sols := { y2, x-1 }, { y , x2 }
2
> assign(sols[1]); x; y;
-1
2
> sols[2];
1
{ 2 , -12 }
2
> assign(sols[2]); x; y;
Error, (in assign) invalid arguments
-1
2
_____________________________________________________________________
Program Studi Matematika
Jurusan Matematika FMIPA Universitas Brawijaya
BAB II OPERASI DASAR MAPLE
13
_____________________________________________________________________
Penugasan sementara ke variabel matematika dapat dilakukan dengan fungsi subs.
Fungsi ini memungkinkan
untuk mengevaluasi suatu ekspresi tanpa merubah
variabel matematika ke variabel program:
> z; #z adalah variabel matematika
z
> f:=cos(z);
> subs(z=Pi/4,f);
> eval(%);
> z;
f := cos( z )

cos 
4
2
2
#Cek bahwa z masih merupakan variabel matematika
z
_____________________________________________________________________
Program Studi Matematika
Jurusan Matematika FMIPA Universitas Brawijaya