Signal modelling - Universitas Dian Nuswantoro

Signal Models
{Rangkaian Elektrik}
By: Gutama Indra Gandha, M.Eng
Program Studi Teknik Elektro
Fakultas Teknik
Universitas Dian Nuswantoro
Tujuan perkuliahan
• Mahasiswa mampu membuat model matematis sinyal
• Mahasiswa dapat mengetahui bentuk sebuah sinyal berdasarkan model
matematis
• Mahasiswa dapat memanipulasi sebuah sinyal dengan menggunakan model
matematis
TOOL – MATLAB
MATERI PERKULIAHAN
•
•
•
•
Konsep gelombang
Fungsi Gelombang Eksponensial
Fungsi Gelombang Sinus
Gelombang komposit
 Sinus Decaying
 Sinus Growing
Konsep gelombang
• Bentuk gelombang adalah sebuah persamaan yang menyatakan sinyal sebagai
fungsi dari waktu
t
Fungsi Gelombang
𝑓(𝑡)
[0,1,2,3,4,5…]
Fungsi f(t) dapat bervariasi.
Misalkan : fungsi eksponensial, fungsi sinus
atau fungsi komposit
FUNGSI GELOMBANG
EKSPONENSIAL
• Fungsi ekponensial adalah sebuah fungsi yang mempunyai component utama
bilangan Euler (e) berpangkat. Fungsi ini dapat membentuk sebuah fungsi
turun (decay) dan fungsi naik (growth) tergantung dari nilai konstanta
pangkat.
𝑡
𝑦 𝑡 =𝑒
dimana nilai
e ≈ 2.71828...
Terdapat dua jenis fungsi eksponensial yaitu fungsi eksponensial naik (growth) dan fugsi eksponensial
turun (decay)
Growth & Decay
𝑦 𝑡 = 𝑒 −𝑡
𝑦 𝑡 = 𝑒𝑡
Reff : eksponensial_decay.m & eksponensial_growth.m
Manipulasi laju pada sinyal eksponensial
𝑣 𝑡 = 𝑒𝑡
𝑣 𝑡 =
𝑡
𝑒𝜏
Laju konstan atau tidak dapat dimanipulasi
Laju dapat dimanipulasi dengan mengubah nilai 𝜏
PARAMETER
𝑉𝐴
𝜏
𝑡
𝑣 𝑡 =
−𝑡
𝑉𝐴 𝑒 𝜏
𝑣 𝑡 =
−𝑡
5𝑒 2
𝑉𝐴 adalah amplitude maksimal
t adalah waktu
𝜏 adalah kecepatan penurunan sinyal (decay rate)
Reff : eksponensial_singletao_decay.m
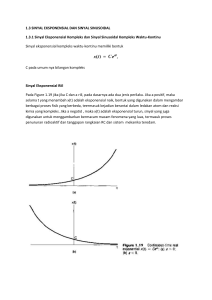
Decaying rate
𝑣 𝑡 =
−𝑡
5𝑒 𝜏
Garis biru adalah 𝑣 𝑡 = 5𝑒
−𝑡
2
Garis m𝐞𝐫𝐚𝐡 adalah 𝑣 𝑡 = 5𝑒
Garis kuning adalah 𝑣 𝑡 = 5𝑒
−𝑡
4
−𝑡
6
Semakin besar nilai 𝝉 maka semakin lambat
laju penurunan sinyalnya.
Reff : eksponensial_multitao_decay.m
Growing rate
𝑣 𝑡 =
𝑡
𝜏
5𝑒
Garis biru adalah 𝑣 𝑡 = 5𝑒
𝑡
2
Garis m𝐞𝐫𝐚𝐡 adalah 𝑣 𝑡 = 5𝑒
Garis kuning adalah 𝑣 𝑡 = 5𝑒
𝑡
4
𝑡
6
Semakin besar nilai 𝝉 maka semakin lambat
laju penurunan sinyalnya.
Reff : eksponensial_multitao_growth.m
FUNGSI GELOMBANG
SINUS
Fungsi sinus adalah sebuah fungsi yang memebntuk perulangan dari suatu osilasi antara dua nilai puncak.
𝑣 𝑡 = 𝑉𝐴 cos(𝜔𝑡) dimana
𝑇0
𝑣 𝑡 = 𝑉𝐴 cos(2𝜋𝑓𝑡) karena
𝜔 = 2𝜋𝑓
𝑓=
1
𝑇0
maka
𝒗 𝒕 = 𝑽𝑨 𝐜𝐨𝐬 𝟐𝝅𝒕/𝑻𝟎
Dimana 𝑇0 adalah waktu yang diperlukan untuk membuat
satu gelombang penuh (periode)
𝑣 𝑡 = 𝑉𝐴 cos 2𝜋𝑡/𝑇0
𝑣 𝑡 = 𝑉𝐴 cos(2𝜋𝑓𝑡)
Ref : sinus_f.m dan sinus_t.m
Pergeseran Fase (t based)
Ref : sinus_t_geserwaktu.m
Pada gelombang sinus pegeseran fasa dapat
dinyatakan dalam waktu (𝑇𝑠 ).
𝑣 𝑡 = 𝑉𝐴 cos 2𝜋(𝑡 − 𝑇𝑠 )/𝑇0
𝑣 𝑡 = 5 cos 2𝜋𝑡/0.5
….. Blue line (no Ts)
2𝜋 𝑡 − 0.1
𝑣 𝑡 = 5 cos
0.5
….. Red line ( Ts)
Pergeseran Fase (∅ based)
Ref : sinus_t_gesersudut.m
Pergeseran fase juga dapat dinyatakan dengan sudut (∅).
𝑣 𝑡 = 𝑉𝐴 cos
Dimana
2𝜋𝑡
−∅
𝑇0
atau
𝑣 𝑡 = 𝑉𝐴 𝑐𝑜𝑠2𝜋𝑓 − ∅
1
𝑓=
𝑇0
𝑣 𝑡 = 𝑉𝐴 cos 2𝜋𝑓
(warna biru)
𝑣 𝑡 = 𝑉𝐴 cos 2𝜋𝑓 + ∅
(warna merah)
Fase juga dapat dinyatakan secara waktu : ∅ = 2π
𝑇𝑠
𝑇0
Gelombang Komposit
Gelombang komposit adalah gelombang yang dibentuk dari beberapa gelombang dasar .
Parameter – parameter yang terdapat pada gelombang komposit merupakan gabungan dari komponen
gelombang penyusunnya.
Sinus – Exponential (growth)
Ref : eksponensial_multitao_growth.m
𝑣𝑎 𝑡 = 𝑉𝑥 sin(2𝜋𝑓𝑡)
𝑣𝑏 𝑡 =
𝑡
𝜏
𝑉𝑦 𝑒
𝑣𝑘 𝑡 = 𝑉𝑥 sin(2𝜋𝑓𝑡) ∗
𝑡
𝜏
𝑉𝑦 𝑒
Contoh : Diketahui dua buah sinyal sinus dan
eksponensial berikut ini:
𝑣𝑎 𝑡 = 1 sin(2𝜋5𝑡)
𝑣𝑏 𝑡 =
𝑡
5𝑒 2
Sehingga jika dua gelombang di kompositkan akan
menjadi seperti berikut ini:
𝑡
2
𝑣𝑘 𝑡 = 5𝑒 . sin(2𝜋5𝑡)
Sinus – Exponential (decay)
eksponensial_multitao_decay.m
𝑣𝑎 𝑡 = 𝑉𝑥 sin(2𝜋𝑓𝑡)
𝑣𝑏 𝑡 =
−𝑡
𝑉𝑦 𝑒 𝜏
𝑣 𝑘 = 𝑉𝑥 sin(2𝜋𝑓𝑡) ∗
−𝑡
𝑉𝑦 𝑒 𝜏
Contoh : Diketahui dua buah sinyal sinus dan
eksponensial berikut ini:
𝑣𝑎 𝑡 = 1 sin(2𝜋5𝑡)
𝑣𝑏 𝑡 =
−𝑡
5𝑒 2
Sehingga jika dua gelombang di kompositkan akan
menjadi seperti berikut ini:
−𝑡
2
𝑣𝑘 𝑡 = 5𝑒 . sin(2𝜋5𝑡)
Parameter gelombang komposit
Parameter gelombang komposit ditentukan oleh parameter gelombang penyusunnya. Masing –
masing parameter gelombang memiliki pengaruh tertentu pada gelombang komposit.
𝑉𝑥
𝑉𝑦
𝜏
𝑣 𝑡 = 𝑉𝑥 sin(2𝜋𝑓𝑡) ∗
𝑓
𝑡
𝑉𝑦 𝑒 𝜏
Perbandingan sinyal output 𝑣𝑥 = 1 dan 𝑣𝑥 = 2
Ref : komposit_sinus_exp_vx.m
Implementasi
Aplikasi embedded signal generator
Model singnal ditanamkan ke embedded system untuk dapat menghasilkan signal sesuai dengan
parameter input
𝑣𝑥
MCU (Microcontroller Unit)
𝑣 𝑡 = 𝑉𝑥 sin(2𝜋𝑓𝑡) ∗
t
𝑡
𝑉𝑦 𝑒 𝜏
DAC
(Digital to
Analog
Converter)