FASOR DAN ELEMEN-ELEMEN DASAR RANGKAIAN LISTRIK

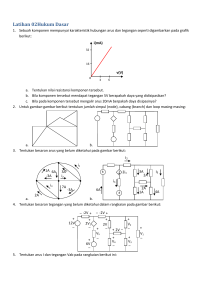
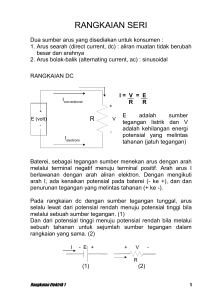
RANGKAIAN SERI
1. Pendahuluan
Dua elemen dikatakan terhubung seri jika :
a. Kedua elemen hanya mempunyai satu terminal bersama.
b. Titik bersama antara elemen tidak terhubung ke elemen yang lain.
Pada Gambar 1 resistor R1 dan R2 adalah seri karena keduanya
mempunyai titik bersama yaitu b. Ujung lain dari resistor dihubungkan ke
titik lain dalam rangkaian. Untuk alasan yang sama, baterei E dan resistor
R1 adalah seri dengan terminal a titik bersama, dan resistor R 2 dan baterei
adalah seri dengan terminal c sebagai titik bersama. Dengan demikian
ketiga elemen tersebut adalah terhubung seri.
Jika rangkaian pada Gambar 1(a) dimodifikasi sedemikian rupa
sehingga resistor R3 ditambahkan pada titik bersama b seperti yang
perlihatkan pada Gambar 1(b) maka R1 dan R2 tidak lagi seri karena tidak
terpenuhi lagi dua definisi di atas sebagai rangkaian seri.
Gambar 1. (a) Rangkaian seri; (b) kondisi dimana R1 dan R2 tidak seri
Rangkaian Listrik I by zaenab muslimin
30
Arus dalam hubungan seri adalah sama
Sebuah cabang dari suatu rangkaian memiliki satu atau lebih
elemen yang terhubung seri. Pada Gambar 1(a) R1 adalah cabang dari
suatu rangkaian, R2 adalah cabang yang lain dan baterei adalah
merupakan cabang ketiga.
Perhatikan bahwa resistansi total dari suatu rangkaian adalah
resistansi dilihat dari sumber ke dalam rangkaian kombinasi seperti yang
ditunjukkan pada Gambar 2.
Gambar 2. Resistansi total dilihat dari sumber
Untuk elemen rangkaian yang terhubung seri arusnya adalah
sama maka tegangan masing-masing resistor dapat dihitung dengan
menggunakan hukum Ohm,
V1 = I. R1 , V2 = I.R2 , ..., VN = I .RN ..........................................(1)
Daya yang dikirim ke masing-masing resistor dapat ditentukan
dengan menggunakan salah satu dari ketiga persamaan berikut, untuk R1
V12
P1  V1 I1  I R 1 
R1
2
1
...............................................................(2)
Daya yang dikirim oleh sumber adalah :
P = E. I ...............................................................................................(3)
Total daya yang di kirim ke rangkaian resistif sama dengan total daya
yang di disipasi untuk elemen-elemen resistif yaitu :
Ptot = P1 + P2 + P3 + ...+ PN
Rangkaian Listrik I by zaenab muslimin
.....................................................(4)
31
2. Sumber Tegangan Hubungan Seri
Sumber tegangan dalam hubungan seri diperlihatkan pada
Gambar 3, dimana pada Gambar 3(a) sumber tegangan saling
memperkuat sehingga tegangan total sbb,
Etot = E1 + E2 + E3 = 10 + 6 + 2 = 18 volt
Sedangkan untuk Gambar 3(b) tegangan total adalah
Etot = E2 + E3 – E1 = 9 + 3 - 4 = 8 volt
Gambar 3. Sumber tegangan total
3. Hukum Kirchhoff Tentang Tegangan Pada Lintasan Tertutup
Hukum Kirchhoff untuk lintasan yang tertutup dapat dinyatakan
sebagai berikut :
Jumlah seluruh jatuh potensial /tegangan /beda potensial
pada suatu jerat/loop sama denga nol.
Secara matematik dapat dituliskan
 (JP) loop  0
............................................................................(5)
JP adalah jatuh potensial, yaitu beda potensial dari satu titik ke titik
lainnya. Positif bila kita berpindah dari titik yang berpotensial lebih tinggi
Rangkaian Listrik I by zaenab muslimin
32
ke titik yang potensialnya lebih rendah dan negatif bila sebaliknya.
Perhatikan Gambar 4 berikut ini.
Gambar 4. Beda potensial pada setiap elemen dan jerat
Menurut hukum Kirchhoff, untuk jerat ABEFA berlaku: VAB + VBE +
VEF + VFA = 0. Karena VAF = V1 , maka VFA = -V1 , sehinga persamaan
menjadi : VAB + VBE + VEF - V1 = 0 atau : VAB + VBE + VEF = V1. Demikian
juga berlaku untuk jerat ABCDGFA berlaku :
VAB + VBC + VCD + VDG + VGF + VFA = 0
Karena VCD = V2, VGF = -V3 dan VFA = -V1 , maka :
VAB + VBC + V2 + VDG – V3 – V1 = 0. atau
VAB + VBC + VDG = V1 + V3 – V2 .
Demikian pula untuk setiap jerat lainnya dapat dituliskan hukum
Kirchhoff yang sesuai untuk masing-masingnya. Sekarang kita ganti
elemen-elemen pasif pada rangkaian Gambar 4 dengan R, L dan C
tertentu seperti pada Gambar 5.
Untuk jerat ABEFA persamaan jerat akan berbentuk :
t
1
R 1 i 1  VC (0)   i C dt  R 4 i 4  V1  0 atau
C0
t
1
R 1 i 1  VC (0)   i C dt  R 4 i 4  V1
C0
Rangkaian Listrik I by zaenab muslimin
33
Untuk jerat BCDEB persamaannya adalah :
R 2 i 2  V2  L
t
di L
1
 VC (0)   i C dt  0 atau
dt
C0
t
di L
1
R2 i2  L
 VC (0)   i C dt   V2
dt
C0
Gambar 5. Jatuh potensial antar simpul dan arus cabang
Untuk jerat DGFED persamaan hukum Kirchhoff mengenai beda
potensial adalah :
R 3 i 3  V3  R 4 i 4  L
R3 i3  R4 i4  L
di L
 0 atau
dt
di L
 V3
dt
Contoh 1
Tentukanlah tegangan yang tidak diketahui pada Gambar 6.
Contoh 2
Tentukanlah tegangan V1 dan V2 untuk rangkaian pada Gambar 7.
Rangkaian Listrik I by zaenab muslimin
34
Gambar 6. Contoh 1
Gambar 7. Contoh 2
4. Aturan Pembagi Tegangan
Metode pembagi tegangan adalah suatu cara untuk menentukan
tegangan tanpa mencari arus terlebih dahulu. Aturannya dapat diturunkan
dari rangkaian pada Gambar 8.
RT = R1 + R2
dan
Rangkaian Listrik I by zaenab muslimin
I = E / RT
35
Gunakan hukum Ohm,
 E
V  IR  
1
1 R
 T

R E
R  1
dan
 1 R
T

 E 
R E
R  2
V  IR  
2
2 R  2 R
T
 T
Bentuk umum aturan pembagi tegangan adalah :
R
V  x .E
x R
T
...........................................................................(6)
Gambar 8. Aturan pembagi tegangan
Contoh 3
Gunakan aturan pembagi tegangan, untuk menentukan V 1 dan V3 untuk
rangkaian seri pada Gambar 9..
Gambar 9. Contoh 3
Rangkaian Listrik I by zaenab muslimin
36
5. Notasi Sumber Tegangan dan Ground
Simbol untuk hubungan dengan ground diperlihatkan pada
Gambar 10 dimana beda potensial adalah 0 volt.
Gambar 10. Potensial ground
Bila Gambar 1 dihubungkan dengan ground maka dapat
digambarkan seperti pada Gambar 11(a), (b), dan (c). Telah diketahui
bahwa terminal negatif dari baterei dan ujung resistor R2 di hubungkan ke
ground. Meskipun Gambar 11(c) menunjukkan tidak ada hubungan antara
dua ground, namun keduanya terhubung sedemikian rupa sehingga
muatan tetap dapat mengalir. Jika E=12 V, maka titik a adalah positif 12 V
terhadap potensial ground dan 12 V adalah seri dengan kombinasi R1 dan
R2.
Gambar 11. Tiga cara menggambar rangkaian dc seri yang sama
Sumber tegangan yang diperlihatkan pada Gambar 12(a) dan
Gambar 13(a) dapat diillustrasikan seperti pada Gambar 12(b) dan
Gambar 13(b).
Rangkaian Listrik I by zaenab muslimin
37
Gambar 12. Penempatan notasi khusus untuk sumber tegangan dc
dengan simbol standar
Gambar 13. Penempatan notasi untuk suplai dc negatif dengan notasi
standar
Notasi Subskrip Ganda
Tegangan dinyatakan antara dua titik, sehingga memiliki notasi
subskrip ganda dimana subskrip pertama sebagai potensial tertinggi.
Perhatikan Gambar 14(a), dua titik a dan b yang didefinisikan sebagai
tegangan pada resistor R. Karena a adalah subskrip pertama untuk Vab,
maka titik a harus mempunyai potensial yang lebih tinggi dari pada titik b,
hal ini memungkinkan bila Vab bernilai positif. Jika ternyata titik b lebih
potensial daripada titik a maka Vab bernilai negatif, sebagaimana
ditunjukkan pada Gambar 14(b).
Rangkaian Listrik I by zaenab muslimin
38
Gambar 14. Definisi tanda untuk notasi subskrip ganda
Notasi Subskrip Tunggal
Jika titik b dari notasi Vab ditentukan sebagai potensial ground (0
volt), maka notasi subskrip tunggal dapat digunakan yaitu tegangan pada
titik a terhadap ground. Pada Gambar 15, Va adalah tegangan dari titik a
terhadap ground, yang bernilai 10 V dan Vb adalah tegangan dari titik b
terhadap ground yang nilainya 4 V pada tahanan 4 ohm.
Gambar 15. Definisi penggunaan notasi subskrip tunggal
6. Resistansi Internal Sumber Tegangan
Setiap sumber tegangan apakah generator dc, baterei, atau
suplai yang digunakan pada laboratorium yang diperlihatkan pada
Gambar 16(a) akan memiliki resistansi internal dan rangkaian ekivalen
ketiga sumber tegangan tersebut digambarkan seperti pada Gambar
16(b).
Rangkaian Listrik I by zaenab muslimin
39
Gambar 16. (a) Sumber tegangan dc; (b) rangkaian ekivalen
Sumber tegangan yang telah dibahas sebelumnya adalah sumber
tegangan ideal (tanpa resistansi internal) seperti yang diperlihatkan pada
Gambar 17(a). Pada Gambar 17(b) diperhitungkan pengaruh dari
resistansi internal, tegangan output akan E volt jika IL=0 (tanpa beban).
Bila sebuah beban dihubungkan ke rangkaian seperti pada Gambar 17(c)
tegangan output dari sumber tegangan akan menurun karena terjadi drop
tegangan pada resistansi internal. Dengan menerapkan hukum Kirchhoff
tentang beda potensial pada Gambar 17(c) maka diperoleh :
E – IL Rint –VL = 0
VNL – IL Rint –VL = 0
karena
E = VNL
maka,
dan VL = VNL – IL Rint .............................(7)
Gambar 17. Sumber tegangan (a) ideal, Rint=0 (b) menentukan VNL (c)
menentukan Rint
Jika nilai Rint tidak diketahui, maka dapat ditentukan dengan
menyederhanakan persamaan (7) yaitu :
R int 
VNL  VL VNL IL R L VNL



 R L .....................................(8)
IL
IL
IL
IL
Rangkaian Listrik I by zaenab muslimin
40
Gambar 18. VL versus IL untuk generator dc dengan Rint = 2 Ω
Grafik tegangan output sebagai fungsi arus tampak pada Gambar
18. Setiap kenaikan beban menyebabkan losses tegangan pada resistansi
internal juga naik dan mengakibatkan tegangan pada terminal menurun.
Arus maksimum yang dinyatakan sebagai IFL menyebabkan tegangan
pada resistansi internal adalah Vint=(10)(2) = 20 V dan tegangan terminal
akan menurun menjadi 100 V, sedangkan idealnya diharapkan bahwa
generator dc tetap memberikan tegangan 120 V dari titik di bawah arus
beban penuh hingga mencapai arus beban penuh. Konsekuensi langsung
dari losses tegangan output adalah losses daya yang di kirim ke beban.
Kalikan kedua sisi pada persamaan (7) dengan IL diperoleh :
IL VL
Daya beban
=
IL VNL
output daya baterei
-
I2L Rint .................................(9)
rugi daya dalam bentuk panas
7. Regulasi Tegangan
Idealnya untuk setiap sumber tegangan diharapkan bahwa untuk
range/daerah permintaan beban (IL), tegangan tetap konstan. Dengan
kata lain, jika sumber tegangan di set 12 V, maka diinginkan tegangan
terminal tetap konstan yaitu sebesar 12 V meskipun arus berubah-ubah.
Untuk mengukur bagaimana kondisi sumber tegangan terhadap kondisi
ideal diberikan oleh karakteristik regulasi tegangan. Regulasi tegangan di
definisikan sebagai suplai antara batas kondisi tanpa beban dan kondisi
beban penuh (Gambar 19) dan dapat dituliskan seperti persamaan
berikut;
Rangkaian Listrik I by zaenab muslimin
41
Voltage regulation (VR) % 
VNL  VFL
x 100% ....................(10)
VFL
Gambar 19. Definisi regulasi tegangan
Untuk kondisi ideal VFL = VNL dan VR (%) =0. Oleh karena itu semakin
kecil regulasi tegangan semakin kecil pula perubahan tegangan terhadap
perubahan beban. Regulasi tegangan dapat dituliskan pula sebagai
berikut :
VR (%) 
R int
x 100%
RL
........................................................(11)
Dengan kata lain semakin kecil resistansi internal untuk beban sama,
semakin kecil regulasi dan lebih mendekati output yang ideal.
8. Teknik Pengukuran
Ammeter ditempatkan seri dengan cabang dimana arus ingin
diukur (lihat Gambar 20)
Gambar 20. Hubungan seri dari sebuah ammeter
Rangkaian Listrik I by zaenab muslimin
42
Jika resistansi meter mendekati atau melebihi 10% dari R
(Gambar 20) maka akan berpengaruh pada pengukuran arus, karena
kenyataannya bahwa resistansi meter betambah dengan turunnya arus.
Umumnya dapat diasumsikan bahwa resistansi internal ammeter adalah
cukup kecil dibandingkan resistansi elemen rangkaian yang lain sehingga
dapat diabaikan.
Untuk memperoleh pembacaan yang positif maka ammeter harus
dihubungkan dengan arus masuk pada terminal + meter dan
meninggalkan terminal – seperti pada Gambar 21.
Gambar 21. Hubungan ammeter untuk memperoleh pembacaan positif
Voltmeter selalu ditempatkan paralel dengan elemen dimana
tegangan akan di ukur.
Pembacaan
positif
pada
voltmeter
diperoleh
dengan
menghubungkan terminal + ke titik yang potensialnya lebih tinggi dan
terminal negatif dihubungkan ke potensial yang lebih rendah, seperti pada
Gambar 22.
Gambar 22. Hubungan voltmeter untuk memperoleh pembacaan positif
Rangkaian Listrik I by zaenab muslimin
43
Untuk notasi subskrip ganda, selalu jamper warna merah
dihubungkan ke subskrip pertama dan jamper warna hitam ke subskrip
kedua. Untuk mengukur tegangan Vab pada Gambar 23, hubungkan
jamper merah ke titik a dan jamper hitam ke titik b. Untuk notasi subskrip
tunggal, jamper merah ke titik subskrip tunggal dan jamper hitam ke
ground seperti pada Gambar 23 untuk Va dan Vb .
Gambar 23. Pengukuran tegangan dengan subskrip ganda dan subskrip
tunggal
Resistansi internal dari suplai tidak dapat di ukur dengan
ohmmeter karena ada voltmeter. Tegangan tanpa beban dapat di ukur
dengan menempatkan voltmeter seperti pada Gambar 24(a). Resistansi
internal voltmeter biasanya cukup tinggi sehingga arus yang dihasilkan
kecil dan dapat diabaikan. Ammeter dapat ditempatkan langsung pada
suplai seperti pada Gambar 24(b) untuk mengukur ISC dan Rint dapat
ditentukan dengan menggunakan hukum Ohm : R int = ENL / ISC. Karena
resistansi internal dari suplai sangat rendah maka hasil pengukuran akan
diperoleh arus yang besar yang dapat merusak meter, suplai dan akan
berbahaya. Oleh sebab itu Gambar 24(b) tidak dianjurkan. Pendekatan
yang baik adalah menggunakan resistansi beban yang akan
menghasilkan arus suplai kira-kira setengah dari nilai nominal maksimum
dan mengukur tegangan terminal kemudian gunakan persamaan (8) untuk
menentukan Rint.
Rangkaian Listrik I by zaenab muslimin
44
Gambar 24.(a) Mengukur tegangan tanpa beban E; (b) mengukur arus
short-circuit
Rangkaian Listrik I by zaenab muslimin
45