Gaya gravitasi memengaruhi gerakan planet

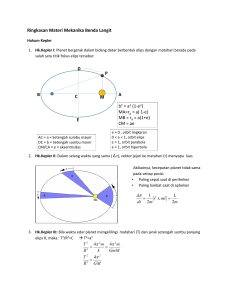
Gaya gravitasi memengaruhi gerakan planet-planet dan benda-benda angkasa
lainnya. Selain itu, gaya gravitasi juga penyebab mengapa semua benda jatuh menuju
permukaan bumi. Keteraturan gerak planet dalam tata surya dijelaskan oleh
Copernicus dan hukum Keppler. Keppler mengungkapkan tiga kaidah mengenai gerak
planet, yang sekarang dikenal sebagai hukum I, II, dan III Kepler. Hukum-hukum
Kepler tersebut adalah :
 Hukum I Kepler
Lintasan setiap planet ketika mengelilingi matahari berbentuk elips, di mana
matahari terletak pada salah satu fokusnya.
Kepler tidak mengetahui alasan mengapa planet bergerak dengan cara
demikian. Pada orbit elips yang dijelaskan pada Hukum I Kepler. Dimensi paling
panjang pada orbit elips disebut sumbu mayor (sumbu utama), dengan setengah
panjang a. Setengah panjang ini disebut sumbu semiutama (semimayor), seperti yang
ditunjukkan pada gambar berikut :
F1 dan F2 adalah titik fokus. Matahari berada pada F1 dan planet berada pada P.
Tidak ada benda langit lainnya pada F2. Total jarak dari F1 ke P dan F2 ke P sama
untuk semua titik dalam kurva elips. Jarak pusat elips (O) dan titik fokus (F1 dan F2)
adalah ea, di mana e merupakan angka tak berdimensi yang besarnya berkisar antara 0
sampai 1, disebut juga eksentrisitas. Jika e = 0 maka elips berubah menjadi lingkaran.
Kenyataanya, orbit planet berbentuk elips alias mendekati lingkaran. Dengan
demikian besar eksentrisitas tidak pernah bernilai nol. Nilai e untuk orbit planet bumi
adalah 0,017. Perihelion merupakan titik yang terdekat dengan matahari, sedangakan
titik terjauh adalah aphelion.
 Hukum II Kepler
Luas daerah yang disapu oleh garis antara matahari dengan planet adalah sama
untuk setiap periode waktu yang sama.
Hal yang paling utama dalam Hukum II Kepler adalah kecepatan sektor mempunyai
harga yang sama pada semua titik sepanjang orbit yang berbentuk elips.
 Hukum III Kepler
Kuadrat waktu yang diperlukan oleh planet untuk menyelesaikan satu kali orbit
sebanding dengan pangkat tiga jarak rata-rata planet-planet tersebut dari matahari.
Jika T1 dan T2 menyatakan periode dua planet, dan r1 dan r2 menyatakan jarak ratarata planet dari matahari, maka :
Newton juga menunjukkan bahwa Hukum III Kepler juga bisa diturunkan secara
matematis dari Hukum Gravitasi Universal dan Hukum Newton tentang gerak dan
gerak melingkar. Sekarang mari kita tinjau Hukum III Kepler menggunakan
pendekatan Newton.
Persamaan Hukum II Newton :
Pada kasus gerak melingkar beraturan, hanya terdapat percepatan sentripetal, yang
besarnya adalah :
Persamaan Hukum Gravitasi Newton :
Sekarang kita masukan persamaan Hukum Gravitasi Newton dan percepatan
sentripetal ke dalam persamaan Hukum II Newton :
m1 adalah massa planet, mM adalah massa matahari, r1 adalah jarak rata-rata planet
dari matahari, v1 merupakan laju rata-rata planet pada orbitnya.
Waktu yang diperlukan sebuah planet untuk menyelesaikan satu orbit adalah T1, di
mana jarak tempuhnya sama dengan keliling lingkaran,2phir1. Dengan demikian,
besar v1 adalah :
Kita masukan persamaan v1 ke dalam persamaan di atas :
Misalnya persamaan 1 diturunkan untuk planet venus (planet 1). Penurunan
persamaan yang sama dapar digunakan untuk planet bumi (planet kedua).
T2 dan r2 adalah periode dan jari-jari orbit planet kedua. Pada persamaan 1 dan
persamaan 2, ruas kanannya memiliki nilai yang sama. Dengan demikian, jika kedua
persamaan ini digabungkan, akan diperoleh :