Pengukuran Besaran Listrik (TC22082) Pertemuan 14

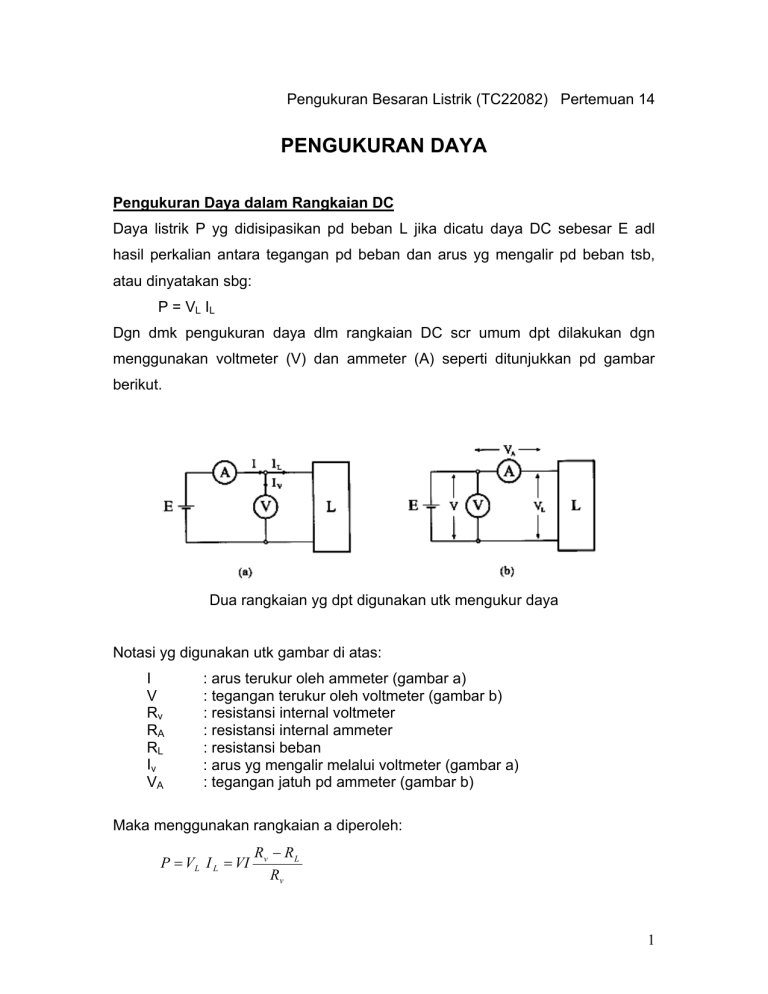
Pengukuran Besaran Listrik (TC22082) Pertemuan 14
PENGUKURAN DAYA
Pengukuran Daya dalam Rangkaian DC
Daya listrik P yg didisipasikan pd beban L jika dicatu daya DC sebesar E adl
hasil perkalian antara tegangan pd beban dan arus yg mengalir pd beban tsb,
atau dinyatakan sbg:
P = VL IL
Dgn dmk pengukuran daya dlm rangkaian DC scr umum dpt dilakukan dgn
menggunakan voltmeter (V) dan ammeter (A) seperti ditunjukkan pd gambar
berikut.
Dua rangkaian yg dpt digunakan utk mengukur daya
Notasi yg digunakan utk gambar di atas:
I
V
Rv
RA
RL
Iv
VA
: arus terukur oleh ammeter (gambar a)
: tegangan terukur oleh voltmeter (gambar b)
: resistansi internal voltmeter
: resistansi internal ammeter
: resistansi beban
: arus yg mengalir melalui voltmeter (gambar a)
: tegangan jatuh pd ammeter (gambar b)
Maka menggunakan rangkaian a diperoleh:
P = VL I L = VI
Rv − RL
Rv
1
Sedangkan menggunakan rangkaian b diperoleh:
P = VL I L = VI
RL − R A
RL
Jika Iv << I dan VA << V, maka
Iv
RL
R
=
≅ L ≅0
I
RV + RL Rv
Dan
VA
RA
R
=
≅ A ≅0
V
R A + RL RL
Sehingga kedua persamaan utk daya menjadi
P = VL I L = VI
Pengukuran Daya dalam Rangkaian AC
Jika rangkaian dicatu sumber listrik AC, maka daya listrik didefinisikan sbg
tegangan jatuh pd beban dikalikan dg arus yg mengalir padanya sbg fungsi:
p(t) = v(t) i(t)
dan biasa disebut dgn daya sesaat. Dlm rangkaian AC biasanya dihitung nilai
rata-rata dari daya sesaat pd suatu selang waktu tertentu. Pd rangkaian yg
dicatu tegangan AC yg periodik, rata-rata daya yg didisipasikan pd satu periode T
didefinisikan sbg:
T
P=
1
p(t ) d (t )
T ∫0
Kasus yg paling sederhana adl catu tegangan sinusoidal dgn beban resistif murni
shg v(t) dan i(t) mempunyai fase yg sama dan p(t) diberikan oleh:
p(t) = V I [1 – cos(2ωt)]
dengan V dan I adl nilai rms v(t) dan i(t) serta ω adl frekuensi sudut sumber
tegangan.
Jika beban adl murni reaktif maka tegangan dan arus pd beban mpy beda fase
sebesar 90° shg daya sesaatnya dinyatakan dgn:
p(t) = V I cos(2ωt)
2
Pada umumnya, impedans beban dinyatakan dalam rangkaian ekivalen AC-nya
(yaitu seri anatar resistansi murni dan reaktansi murni). Dengan demikian maka
daya listrik yang didisipasikan dalam beban ZL dapat dinyatakan sebagai
jumlahan komponen daya yang didisipasikan oleh resistansi REQ dan komponen
daya yang didisipasikan oleh reaktansi XEQ karena ZL = REQ + XEQ. Perhatikan
gambar berikut.
Penurunan tegangan pada beban dan komponen ekivalennya
Dengan menganggap tidak ada daya aktif yang didisipasikan dalam reaktansi
XEQ, maka
P = V REQ I L = V L I L cos ϕ
Suku cos ϕ sering disebut dengan faktor daya. Dalam hal ini hanya sebagian dari
tegangan VL yang berkontribusi pada daya, karena komponen VXEQ (jatuh
tegangan pada reaktansi) tidak menghasilkan daya aktif karena komponen tsb
tegak lurus (ortogonal) terhadap arus yang mengalir pada beban IL.
Bagian atau suku
PA = VL IL
disebut yang tampak (apparent power), sedangkan bagian atau suku
Q = VXEQ IL = VL IL sin ϕ
disebut
daya reaktif karena mrpk kuantitas yg secara dimensional ekivalen
dengan daya. Dari gambar di atas hubungan antara daya aktif, daya reaktif, dan
daya yang tampak dapat dinyatakan sebagai:
PA = P 2 + Q 2
3
Metode Tiga Voltmeter
Untuk frekuensi rendah dan medium, pengukuran daya dapat dilakukan
menggunakan metode tiga voltmeter seperti diperlihatkan pada rangkaian
berikut.
Metode tiga voltmeter
Daya yang didisipasikan pada beban L dapat diukur menggunakan resistor
noninduktif R kemudian mengukur tiga tegangan seperti diperlihatkan pada
gambar. Maka
V AC = VL + R I L
2
V AC
= R 2 I L2 + V L2 + 2 RV L I L
Dan daya yang didisipasikan dalam beban L dinyatakan sbg:
PL =
2
2
2
2
V AC
− R 2 I L2 − V L2 V AC
− V AB
− V BC
=
2R
2R
Thermal Wattmeter
Rangkaian dasar thermal wattmeter ditunjukkan pada gambar berikut. Tanpa
beban maka:
i1 = i2 =
ip
2
=
v
2R + r
Dengan menambahkan beban L maka besarnya i1 dan i2 tidak lagi sama
(imbalance), dan hubungannya mjd:
i1 − i2 =
S iL
2R
4
Voltmeter mengukur tegangan imbalance Δe yang sebanding dengan daya aktif
yang diserap oleh beban yaitu:
[
] [
Δe = k (i1 ) 2 − (i2 ) 2 = k (i p + i L ) 2 − (i p − i L ) 2
]
= k (4 i p i L )
= k1 v(t ) i (t )
= k1 P
(a) Thermal wattmeter (b) Karakteristik operasi pada kondisi ideal
Faktor Daya
Dalam situasi nyata dimana gelombang arus dan/atau tegangan tidak berupa
sinus murni atau beban tidak resistif murni sehingga pernyataan untuk daya tdk
lagi sederhana, atau daya aktifnya biasanya lebih kecil daripada perkalian antara
tegangan rms dan arus rms.
PA ≤ Vrms Irms
Perkalian antara tegangan rms dan arus rms disebut daya yang tampak atau
sering disebut U shg dpt dinyatakan kembali sbg:
U = Vrms Irms
Faktor daya FP digunakan utk menyatakan hubungan antara daya aktif PA dan
daya yang tampak U atau dinyatakan:
FP =
PA
U
Sehingga besarnya faktor daya adalah berada pd jangkauan nol dan satu.
5
Perhatikan gambar berikut.
Diagram phasor untuk arus dan tegangan
Arus I yang mempunyai sudut relatif θ terhadap tegangan E dapat diuraikan
menjadi dua komponen yaitu I cos θ dan I sin θ. Komponen arus yang searah
dengan tegangan E yaitu I cos θ dikalikan dengan tegangan akan menghasilkan
daya rata-rata dalam satuan watt, atau
PA = E I cos θ
PA sering disebut daya aktif atau daya riil atau delivered power.
Komponen arus yang tegak lurus terhadap tegangan E yaitu I sin θ dikalikan
dengan tegangan akan menghasilkan daya reaktif atau sering disebut wattless
component, atau
Q = E I sin θ
Q sering disebut daya reaktif atau daya imajiner atau daya wattless atau daya
magnetisasi. Daya reaktif dinyatakan dalam satuan voltamperes reaktif atau vars.
Jika beban induktif maka arus akan lagging terhadap tegangan dan daya reaktif
mempunyai tanda positif. Jika beban kapasitif maka arus akan leading terhadap
tegangan dan daya reaktif mempunyai tanda negatif.
Diagram phasor untuk daya aktif dan daya reaktif
6
Maka
S = P2 + Q2
Dan
FP =
P
watt
=
= cos θ
S voltampere
Sudut fase gelombang sinus. Dua gelombang yang memotong sumbu mendatar
scr bersamaan adalah sefase. Gelombang sinus yg memotong sumbu mendatar
lebih dulu dibanding gelombang referensi disebut leading. Gelombang sinus yg
memotong sumbu mendatar setelah gelombang referensi disebut lagging.
7