model thomas-fermi relativistik skalar untuk molekul

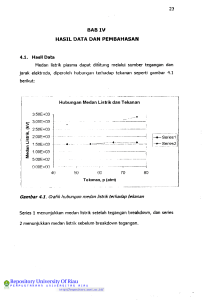
Proseding Seminar Nasional Fisika dan Aplikasinya
Sabtu, 19 November 2016
Bale Sawala Kampus Universitas Padjadjaran, Jatinangor
MODEL THOMAS-FERMI RELATIVISTIK
SKALAR UNTUK MOLEKUL DIATOMIK DALAM
KOORDINAT SFEROIDAL
M. ARIFIN*, A. JAUHARI, D. RUSDIANA
Program Studi Fisika
Fakultas Pendidikan Matematika dan Ilmu Pengetahuan Alam
Universitas Pendidikan Indonesia
Jl. Dr. Setiabudhi No.229 Bandung, Jawa Barat, Indonesia 40154
Abstrak. Kami melaporkan kemajuan penerapan model Thomas-Fermi relativistik
skalar dari teori densitas fungsional untuk mempelajari karakteristik struktur molekuler
dari molekul diatomik. Fungsional energi dasar dari suatu sampel molekul dianalisis
menurut suku-suku fungsional dari fungsi distribusi densitas dari elektron-elektron
dengan mempertimbangkan secara nyata suku-suku energi pertukaran dan korelasi.
Persamaan Kohn-Sham yang dihasilkan dipecahkan secara variasional dalam orbital
molekuler yang diperoleh dari orbital atomik tipe-LCAO (linearized combination of
atomic orbital) yang dinyatakan dalam representasi koordinat sferoidal dengan
menerapkan prosedur metode medan konsisten mandiri (SCF: self-consistent field).
Dengan menggunakan parameter energi terhitung dalam pendekatan densitas lokal
(LDA: local density approximation) dan pendekatan gradien tergeneralisasi (GGA:
generalized gradient approximation) kami mencoba mendeskripsikan secara saksama
data eksperimental dari fungsi-fungsi distribusi densitas dari muatan listrik dan materi
dari material sampel.
Kata kunci: Model Thomas-Fermi relativistik skalar, teori densitas fungsional, molekul
orbital tipe-LCAO, persamaan Kohn-Sham, aproksimasi LDA dan GGA.
Abstract. We report the progress of the application scalar relativistic Thomas-Fermi
(TF) model of the density functional theory (DFT) to study molecular structure
characteristics of diatomic molecules. The ground state energy functional of a sample
molecule is analyzed in terms of functionals of density distribution function of electrons
which taking into account explicitly the exchange and correlation energy terms. The
resulting Kohn-Sham equations are solved variationally using a type of linearized
combination of atomic orbital (LCAO-type) for the molecular orbitals which are
expressed in spheroidal coordinate representations using the procedures applied in the
self-consistent field (SCF) method. Using the calculated energy parameters of local
density approximation (LDA) and generalized gradient approximation (GGA) we
attempt to describe appropriately the experimental data of density distribution functions
of electronic charge and matter of the sample materials.
Keywords: Scalar relativistic Thomas-Fermi model, density functional theory, LCAOtype of molecular orbital, Kohn-Sham equation, LDA and GGA approximations.
1. Pendahuluan
*
email: [email protected]
Kode Artikel: FT-02
ISSN: 2477-0477
M. Arifin, dkk
Model Thomas-Fermi (TF) dalam teori densitas fungsional (TDF) dikembangkan
secara independen oleh Thomas dan Fermi [1, 2] untuk mempelajari gas fermion.
Studi selanjutnya dilakukan oleh Dirac [3] dan von Weizsäcker [4] dengan
menambahkan faktor koreksi masing-masing untuk energi pertukaran dan energi
kinetik. Model TF yang diperluas dalam kerangka kerja non relativistik telah
dikembangkan dan diterapkan dalam fisika benda-banyak, yang mencakup
diantaranya: atom dan molekul [5, 6, 7, 8], inti atom [9, 10, 11, 12], zat padat dan
material elektronik [13]. Model TF relativistik dikembangkan berdasarkan
penerapan kuantisasi persamaan Dirac [14, 15] dan relativistik DFT untuk sistem
benda-banyak yang diperkenalkan oleh Rajagopal dan Callaway [16-20] dengan
menyatakan teorema Hohenberg-Kohn [21-23] dalam kerangka kerja relativistik,
dimana fungsi distribusi densitas elektron diberikan oleh densitas empat-arus (fourcurrent density) dalam formalisme kuantum elektrodinamika (QED). Pembahasan
terstandar dalam DFT relativistik penuh didasarkan pada penerapan formalisme
QED tersebut yang mencakup koreksi secara substansial tentang transvers
elektromagnetik dan radiatif dalam ruang vektor-empat fungsi densitas arus [19,
20]. Model penerapan DFT relativistik tersebut dapat ditemukan dalam sistem
atomik [19, 20] dan molekuler [24-28] yang menerapkan formalisasi energi
fungsional relativistik Kohn-Sham empat-komponen. Seperti disebutkan dalam
literatur [19] masalah umum dari penerapan formalisasi energi fungsional
relativistik QED empat-komponen yang mencakup seluruh koreksi relativistik
substansial di atas dalam permasalahan nyata sistem benda-banyak, khususnya
untuk menghasilkan parameter data eksperimental, masih menemukan banyak
kendala diantaranya menemukan metode pemecahan secara pasti untuk fungsi
gelombang sistem tersebut seperti dikehendaki teorema Hohenberg-Kohn di atas,
khususnya teorema kedua yang menyatakan bahwa: “the functional that delivers the
ground state energy of the system, delivers the lowest energy if and only if the input
density is the true ground state density” [23]. Dalam makalah ini, kami mengajukan
formalisme operasional dari model Thomas-Fermi relativistik skalar untuk molekul
diatomik dimana persamaan Kohn-Sham relativistik dipecahkan dalam pendekatan
longitudinal [19], ekuivalen dengan pendekatan non relativistik Born-Oppenheimer
[29, 30] yang mencakup koreksi relativistik yang berperan dominan dalam atom
atau molekul berat dan atau dalam keadaan energi cukup tinggi. Orbital molekuler
diatomik diperoleh dari orbital atomik tipe-LCAO (linearized combination of
atomic orbital) [30-33] dengan cara memecahkan aproksimasi persamaan Dirac
untuk komponen potensial eksternal skalar dalam koordinat sferoidal [34] dengan
menerapkan prosedur metode medan konsisten mandiri atau self-consistent field
(SCF) [35-41]. Hamiltonian dari sistem tersebut terdiri atas komponen: potensial
Coulomb satu-benda, potensial Hartree-Fock [35-36], pertukaran dan korelasi [3536], dan koreksi relativistik yang mencakup suku koreksi massa-energi, Darwin dan
spin-orbit [36]. Koreksi transvers elektromagnetik dan radiatif dari elektronelektron dalam sistem molekul diatomik dalam ranah relativistik masing-masing
ditentukan secara perturbatif yaitu dengan mendiagonalisasikan Hamiltonian
transvers orde-satu dan dengan cara menguji elemen matrik tereduksi dari transisitransisi multipol listrik dan magnet [40, 41]. Perluasan model tersebut untuk
mencakup molekul kompleks dapat dilakukan dalam kerangka kerja yang sama
baik melalui pendekatan orbital molekuler tipe-LCAO; seperti metode Hückel
dengan cara menyelesaikan persamaan Hartree-Fock-Roothan [30-33], dan
menggunakan representasi teori group dan simetri maupun teori ligand [31-33].
268
Model Thomas Fermi Relativistik Skalar…
2. Model Thomas-Fermi Relativistik Skalar
Sistem molekuler yang ditinjau terdiri atas dua buah atom dimana kedua intinya
sangat lembam sehingga berjarak relatif tetap satu sama lain mengikuti asumsi
pendekatan Born-Oppenheimer [29, 30]. Hamiltonian sistem molekuler diatomik
tersebut dapat dituliskan sebagai
H=
i, A
f i ,elektron
+
A
A, B
f Ainti
,B +
i , j >i
g ijelektron + V XC ( ; ri ) + K relativistik
(1)
dalam satuan atom: e = e 2 = ! = me 1, = 1 / c = 1 / 137.036 , dan 1 Hartree = 2
Rydberg = 27.2116 eV, dengan
konstanta struktur halus; dimana
f Ainti
,B
ZA
i =1 A=1 riA
M M Z Z
2
A B
A +
A=1B > A R
AB
N N 1
=
i =1 j >i rij
1N
2 i =1
1M 1
=
2 A=1M A
f i ,elektron
=
A
g ijelektron
V
XC
[
; r] =
N M
2
i
E XC [
(r )
]
(2)
(3)
(4)
(5)
K relativistik = K massa-energi + K Darwin + K spin -orbit
=
1
(E V )2
2
2mc
!2
dV
2 2
4m c dr
!2
dV 2
(l s )
+
2 2
r 4m c dr r
(6)
dengan indeks i dan j untuk elektron, N jumlah elektron, indeks A dan B untuk inti,
M jumlah inti, V XC ( ; r ) potensial pertukaran dan korelasi, (r ) fungsi densitas
i
elektron, K
relativistik
koreksi relativistik, Z A, B nomor atom inti A, B, RAB jarak inti A
dan B, E XC [ ] energi pertukaran dan korelasi [pers.(5)], E = + m 0 c 2 [41], energi
total elektron,
energi kinetik total elektron, m0 massa diam elektron, c
kecepatan cahaya, V potensial total sistem molekuler, l bilangan kuantum anguler
elektron dan s bilangan kuantum spin elektron. Elemen matrik suku pertukaran
pers.(4) (potensial Hartree [35, 36]), dapat dihitung menggunakan skema orbital
atomik (tipe-LCAO) terlebih dahulu, yaitu [29, 35-36, 42-44]
269
M. Arifin, dkk
1,2
1
1,2 =
rij
=
(i ) 2* ( j )
*
1
*
1
i , j >i
ri
P
rj
(i ) 2* ( j )
*
1
i , j >i
1
1
(i )P 2 ( j )d
i
d
j
(i ) 2 ( j )d
i
d
j
1
ri
(i ) 2* ( j )
1
rj
1
ri
2
rj
(i ) 1 ( j )d
i
d
(7)
j
sebelum ditransformasikan ke koordinat sferoidal. Dalam pers.(7),
1, 2 ,!
(i, j,!)
orbital-orbital atomik, P operator permutasi dan d i , j ,! elemen infinitesimal ruang
fungsi gelombang . Persamaan harga eigen molekuler yang diperoleh dari
Hamiltonian pers.(1) adalah
H
molekul
=E
molekul
(8)
dengan fungsi gelombang molekul berbentuk [34]
molekul
nm
(
, ,
) = Rnm ( )S nm ( )
sin m
cos m
(9)
dimana n bilangan kuantum utama, m bilangan kuantum magnetik dan γ bilangan
kuantum lainnya, seperti: anguler dan spin; yang diperoleh dari pemecahan
persamaan harga eigen pers.(8). Variabel sferoidal
dan
yang dapat
diasosiasikan masing-masing dengan arah radial dan anguler dalam koordinat bola
memenuhi persamaan transformasi [34]
=
r1 + r2
dan
a
=
r1
r2
(10)
a
dimana r1 dan r2 variabel radial dalam koordinat bola masing-masing untuk atom
1 dan 2 dan a jarak antara inti atom 1 dan 2. Dalam koordinat sferoidal, dengan
menggunakan pers.(1)-(7), pers.(8) dapat dituliskan kembali melalui metode
pemisahan variabel masing-masing untuk molekul tegak (prolate) dan terbaring
(oblate) sebagai berikut [34]
dR mn ( )
d
m2
2
(11)
1
k 2 a 2 2 Rmn ( ) = 0
mn +
2
d
d
1
(
d
d
dan
270
(1
)
2
) dSd ( )
mn
(
+
mn
(1
)
m2
2
)
k 2a2
2
S mn (
)= 0
(12)
Model Thomas Fermi Relativistik Skalar…
d
d
(
d
d
(1
2
) dRd ( )
+1
2
mn
)
dS mn (
d
(
mn
)
+
(1
mn
m2
2
+1
k 2a2
)
m2
2
)
+ k 2a2
2
2
Rmn (
)= 0
(13)
S mn (
)= 0
(14)
dimana mn koefisien-koefisien sparasi, telah ditabulasikan [34] dan k 2 adalah
variabel yang diberikan oleh (dalam satuan atomik)
[
]
k 2 = 2 E V (r ) 2
N M Z
N N 1
M M Z Z
E XC [ ]
A
A B
V (r ) =
+
+
+
A=1B > A R
i =1 A=1 riA
i =1 j >i rij
(r )
AB
2
=
2
4
2(E V )
2
dV
dr
r
+
(15)
(16)
dV 2
(l s)
dr r
(17)
yang seluruhnya, [pers.(15)-(17)], dapat ditransformasikan ke koordinat sferoidal
dengan operator spin-orbit memenuhi persamaan eigen
(l s )
molekul
nm
(
, ,
) = 1 [ j ( j + 1) l (l + 1) s(s + 1)]
2
molekul
nm
(
, ,
).
(18)
Energi kinetik kedua inti atom [suku ke-1 ruas kanan pers.(3)] sangat kecil karena
inti sangat masif ( m p 1840me [35]) dan tidak diperhitungkan dalam pers.(11-14)
memenuhi asumsi Born-Oppenheimer [29, 30], namun demikian, dapat dihitung
dengan menerapkan model klaster dan dengan menggunakan fungsi basis yang
tepat untuk molekul dimana seluruh entitas molekul (elektron dan inti) seluruhnya
bergerak relatif terhadap titik pusat massa bersama [33, 40, 44]. Pers.(11-14) dapat
dipecahkan secara serentak dengan menggunakan metode medan konsisten mandiri
(self-consistent field: SCF) [29, 35-36, 42-44] untuk molekul tegak dan terbaring
untuk menghasilkan karakteristik fungsi gelombang molekul yang
direpresentasikan sebagai [35, 36]
(x1 )
1 (x2 )
2
(x1 )
2 (x2 )
!
"
1 (x N )
"
2 (x N )
!
"
!
1
molekul
=
dengan N jumlah atom dan
1
N!
i
(x1 )
N (x2 )
N
"
N (x N )
(19)
(x ) orbital atomik.
j
Secara umum fungsi densitas elektron diberikan oleh (cetak tebal menyatakan
vektor)
271
M. Arifin, dkk
(r ) =
i
i
(r ) 2
(20)
dan jumlah elektron dalam sistem yang ditinjau adalah
(r )d 3r = N .
(21)
Jumlah elektron yang menghuni suatu keadaan kuantum ke-i, bilangan hunian
(number of occupancy), dengan harga eigen yang bersesuaian i memenuhi
persamaan [45]
1
i
N
(22)
fi = 0 fi 1 i = N .
fi = 0
i
>
N
Keadaan kuantum molekuler dengan bilangan kuantum sama: ni = n , li = l , tetapi
mi = m berbeda, maka keadaan kuantum tersebut terdegenerasi, sebagai
f i f nl / (2l + 1)
i = ni li mi = nl dengan demikian maka terdapat sejumlah 0
elektron. Fungsi densitas elektron dalam keadaan tersebut dipenuhi oleh [45]
(r ) = 1
4
n 1
n =1l =0
nl
f nl
(
nl
;r)
r
f nl = 2(2l + 1)
2
dengan 0
f nl
nl
2(2l + 1)
f nl = 0
nl
>
<
N
nl
=
N
.
(20)
N
Energi pertukaran dan korelasi pers.(5) dapat dihitung dengan menggunakan
persamaan sebagai berikut [46]
E XC [
] = 1 (r )V XChole (r )dr + (r )[Vkin (r )
2
dimana
hole
(r1 ) =
V XC
Vkin (r1 ) =
=
272
1
2
1
1
,
1
2
(r1 , r2 )
r1 r2
Vs,kin (r )]dr
(r1 ) (r2 )
dr2
(r1 )
(21)
(22)
(s1 , x 2 ,!, x N | r1 ) 2 ds1dx 2 ! dx N
(r'1 , r1 ) r ' =r
2 (r1 )
1
1
[ (r1 )]2
8 2 (r1 )
(23)
Model Thomas Fermi Relativistik Skalar…
Vs,kin (r1 ) =
1
2
1
1N
=
2 i =1
s
s
(s1 , x 2 ,!, x N | r1 ) 2 ds1dx 2 ! dx N
mol
i
1/ 2
1
(r1 )
(r1 )
(s1 , x 2 ,!, x N
(24)
2
| r1 ) =
s
(x1 ,!, x N )
(r1 ) / N
(25)
untuk masing-masing keadaan koordinat ruang (r1 ,r2 ) spin s. Persamaan KohnSham yang bersesuaian dengan pers.(11)-(18) untuk keadaan kuantum ke-i dalam
notasi fungsi densitas (r ) diberikan oleh [45]
1
2
2
+ V eff [ ; r ]
dimana
V
eff
[
; r] =
(r )
r r'
d r +V
3
i
ext
(r ) = 0
(26)
E XC [ ]
(r ) +
(r )
(27)
i
dengan V ext (r ) potensial Coulomb oleh inti yang dialami elektron. Persamaan
fungsional molekul keadaan energi dasar dapat dituliskan sebagai [45]
E total [
] = T [ ] + E XC [ ] + E Hartree [ ] +
dimana
E Hartree [
dan energi fungsional kinetik T [
Thomas-Fermi adalah [23]
Z
r
] = 1 (r ) (r') dr 3 d 3 r '
2
r r'
(r )d 3 r
(28)
(29)
] untuk gas elektron serba sama dalam model
TTF [ (r )] =
( )
3
3
10
2 2/3
5/3
(r )dr .
(30)
Suku ke-1 dan ke-2 dalam pers.(27) dalam literatur [35, 36] disebut sebagai
potensial Hartree-Fock. Penghitungan terhadap efek-efek relativistik, seperti:
transvers elektromagnetik dan radiatif dari elektron-elektron dalam sistem
molekuler, masing-masing dilakukan secara perturbatif yaitu dengan
mendiagonalisasikan Hamiltonian transvers orde-satu dan dengan cara menguji
elemen matrik tereduksi dari transisi-transisi multipol listrik dan magnet, prosedur
selengkapnya dapat ditemukan dalam literatur [40, 41]. Dengan menggunakan
fungsi gelombang molekuler tipe-LCAO yang dikonstruksikan dari pers.(9), model
ini dapat diperluas untuk membahas molekul kompleks dengan menggunakan
273
M. Arifin, dkk
representasi teori group dan simetri [31-33], terutama untuk memperoleh
karakteristik molekul kompleks yang terbentuk, baik dengan menerapkan prosedur
model klaster, khususnya untuk sistem beberapa benda (few-body system) [44],
maupun menggunakan pendekatan teras beku (frozen core) Hückel [30, 33], dengan
mengasumsikan keberadaan orbital molekuler tipe-π dan tipe-σ, untuk
memecahkan persamaan Hartree-Fock-Roothan untuk molekul kompleks tersebut.
3. Pendekatan Densitas Lokal (LDA) dan Gradien Tergeneralisasi (GGA)
Berdasarkan fungsi densitas orbital molekuler yang diperoleh dari penerapan
prosedur di atas, parameter data eksperimental molekuler seperti: panjang ikatan,
energi ikat, energi ionisasi, energi afinitas dan sebagainya, dapat ditentukan dengan
menggunakan pendekatan semi empirik, misalnya: LDA dan GGA [23, 47].
Fungsional energi pertukaran dan korelasi pers.(21) dalam literatur [45-47], karena
permasalahan dalam sistem benda-banyak, sebagian atau seluruhnya, diperoleh
secara empirik berdasarkan data eksperimen maupun menggunakan simulasi
numerik (monte carlo) [31]. Upaya yang dilakukan akhir-akhir ini (misalnya: [19,
20, 48]) untuk mencari pemecahan permasalahan tersebut adalah dengan
menggunakan representasi fungsional energi dalam densitas arus ruang-empat yaitu
dengan memecahkan persamaan Dirac [49] dalam empat-komponen potensial
secara utuh. Dalam pendekatan LDA [45, 47] energi pertukaran dan korelasi
didefinisikan sebagai
(31)
E XC LDA[ ] = (r ) XC LDA ( (r ))d 3r
dimana [47]
XC LDA
( )=
X LDA
X LDA
( )=
( )+
C LDA
(
)
3
3
4
2
( )
(32)
1
3
(33)
untuk densitas tinggi dan korelasi lemah (dalam [47]):
ˆ cLDA (n(r )) =
ec2
4
0
a0
(c0 ln rs + c1 + c2 rs ln rs + c3 rs + !) ,
rs << 1
(34)
untuk densitas rendah dan korelasi kuat:
ˆ cLDA (n(r )) =
ec2
4
0
a0
d0
d
d
+ 3 1/ 2 + 42 + ! , rs >> 1
rs rs
rs
(35)
dimana c0 , c1 ,! dan d 0 , d1 ,! , masing-masing adalah koefisien bergantung spin
(korelasi spin) dan parameter yang diperoleh dari fitting data. Indeks s menyatakan
gradien fungsi desitas [47, 50]. Dalam pendekatan GGA fungsional energi dapat
dituliskan sebagai [45]
274
Model Thomas Fermi Relativistik Skalar…
E XC
GGA
[ ] = (r )
XC GGA
( (r ), (r ) )d
3
r
(36)
sedangkan potensial yang bersesuaian untuk fungsional harga energi eigen
XC GGA
( (r ), (r ) ) adalah
V XC
GGA
[
; r] =
3
i =1
(r )
i
XC GGA
( (r ),
(r ) ).
(37)
i
Jika didefinisikan hubungan untuk fungsional energi korelasi dengan spin
terpolarisasi atas ( ) dan bawah ( ) sebagai [50]
E CGGA (n , n
)=
d 3 rn[ec (rs ,
) + H (rs ,
, t )]
(38)
dengan seluruh fungsional kuantitas fisis: n[ec (rs , ) + H (rs , , t )] , ec (rs , ) dan
H (rs , , t ) terdefinisi atau diberikan di dalam referensi [50], maka melalui
hubungan hibrid fungsional energy
(
hyb
E XC
= E Xexact + (1 a ) E XGGA
)
E Xexact + ECGGA
(39)
dengan a parameter data fitting atau sebuah koefisien akselerator konvergensi,
hyb
dapat diperoleh dari
E Xexact misalnya, diperoleh dari data eksperimen dan EXC
pemecahan persamaan (36) dan (37), maka harga EXGGA dapat diperoleh secara
numerik melalui proses iterasi [37-41]. Pendekatan semi empirik lainnya, baik
lokal, semi lokal dan non lokal [50] seperti pendekatan spin densitas lokal (LSD:
local spin density) memiliki karakteristik yang ekuivalen dengan dua pendekatan di
atas, LDA dan GGA, yang dapat ditemukan dalam literatur [47, 50].
4. Kesimpulan
Model Thomas-Fermi relativistik skalar untuk molekul diatomik yang
dikonstruksikan dari aproksimasi persamaan Dirac untuk potensial skalar telah
berhasil diformulasikan secara operasional dalam sistem koordinat sferoidal.
Hamiltonian dari sistem tersebut terdiri atas: potensial Coulomb satu-benda,
potensial Hartree-Fock, fungsional pertukaran dan korelasi, dan koreksi relativistik
yang mencakup suku: massa-energi, Darwin dan spin-orbit. Dengan menggunakan
Hamiltonian tersebut persamaan harga eigen sistem molekuler diatomik yang
direpresentasikan dalam orbital atomik tipe-LCAO (linearized combination of
atomic orbital) dipecahkan dalam koordinat sferoidal untuk memperoleh fungsi
gelombang dan energi eigen sistem molekul tersebut dengan menerapkan metode
medan konsisten mandiri (self-consistent field: SCF). Parameter data eksperimental
dari berbagai jenis karakteristik fisis sistem molekuler dapat ditentukan berdasarkan
fungsi densitas elektron yang diperoleh dengan menggunakan pendekatan baik
lokal, semi lokal atau non lokal, seperti LDA (local density approximation) dan
GGA (generalized gradient approximation) dan jenis pendekatan semi empirik
275
M. Arifin, dkk
lainnya. Perluasan model untuk mencakup molekul kompleks dapat dilakukan
dengan menyatakan fungsi gelombang sistem molekuler yang diperoleh tersebut
dalam representasi group dan simetri baik menggunakan model klaster, terutama
untuk molekul yang terbentuk dari beberapa atom, maupun menggunakan
pendekatan dalam metode teras beku Hückel untuk memecahkan persamaan
Hartree-Fock-Roothan untuk molekul kompleks tersebut.
Ucapan Terima Kasih
Kami mengucapkan terima kasih kepada Direktorat Riset dan Pengabdian
Masyarakat, Direktorat Jenderal Penguatan Riset dan Pengembangan, Kementrian
Riset, Teknologi, dan Pendidikan Tinggi Nomor: 048/SP2H/LT/DPRM/II/2016,
tanggal 17 Februari 2016; atas bantuan pembiayaan yang telah diberikan untuk
menyelesaikan kegiatan penelitian dalam skema Hibah Bersaing tahun anggaran
2016/2017.
Daftar Pustaka
[1]
Thomas, L. H., The calculation of atomic fields, Proc. Camb. Philos. Soc. 23
(1927) 542-548.
[2] Fermi, E., Un metodo statistico per la determinazione di alcune priorieta
dell’atome, Rend. Accad. Naz. Lincei 6 (1927) 602-607.
[3] Dirac, P. A. M., Note on exchange phenomena in the Thomas-Fermi atom,
Proc. Cambridge Philos. Soc. 26 (1930) 376-385.
[4] von Weizsäcker, C. F., Zur Theorie der Kernmassen, Z. Phys. 96 (1935) 431458.
[5] Lieb, Elliott H. and Simon, Barry, The Thomas-Fermi Theory of Atoms,
Molecules and Solids, Advances in Mathematics 23 (1977) 22-116.
[6] Lieb, Elliott H., Thomas-fermi and related theories of atoms and molecules,
Reviews of Modern Physics Vol. 53 No. 4 Part I October 1981.
[7] Benguria, Rafael, Brezis, Haim and Lieb, Elliott, The Thomas-Fermi-von
Weizsäcker Theory of Atoms and Molecules, Commun. Math. Phys. 79 (1981)
167-180.
[8] Parr, R. G. and Yang, W., Density-functional theory of atoms and molecules,
Oxford, Clarendon Press (1989).
[9] Petkov, I. Zh. and Stoitsov, M. V., Nuclear Density Functional Theory,
Oxford, Clarendon Press (1991).
[10] Erler, J., Birge, N., Kortelainen, M., Nazarewicz, W., Olsen, E., Perhac, A.
M. and Stoitsov, M., The limits of the nuclear landscape Nature (London)
486 (2012) 509-512.
[11] Centelles, M., Viñas, X., Barranco, M., Ohtsuka, N., Faessler, Amand, Khoa,
Dao T. and Müther, H., Relativistic extended Thomas-Fermi calculations of
finite nuclei with realistic nucleon-nucleon interactions, Physical Review C
Vol. 47 No. 3 (1993) 1091-1102.
276
Model Thomas Fermi Relativistik Skalar…
[12] Ring, Peter, Covariant density functional theory: applications in exotic nuclei,
(2017) Tersedia: http://nuclear.fis.ucm.es/PDFN/documentos/
P.Ring.Complutense-Dec.pdf
[13] Jones, R. O., Density functional theory: Its origins, rise to prominence, and
future, Reviews of Modern Physics Vol. 87 July-September 2015.
[14] Vallarta, M. S. and Rosen, N., Phys. Rev. 41 (1932) 708.
[15] Jensen, H., Z. Phys. 82 (1993) 794.
[16] Rajagopal, A. K. and Callaway, J., Phys. Rev. B 7 (1973) 1912.
[17] Rajagopal, A. K., J. Phys. C 11 (1978) L943.
[18] MacDonald, A. H. and Vosko, S. H., J. Phys. C, Solid State Phys. 12 (1979)
2977.
[19] Engel, E. and Dreizler, R. M., Relativistic Density Functional Theory,
Tersedia: http://th.physik.uni-frankfurt.de/~engel/papers/ed96.pdf
[20] Engel, E., Müller, H., Speicher, C., Dreizler, R. M., In Density Functional
Theory, NATO Series Series B: Physics Vol. 337 Gross E K U Dreizler R M
Eds., New York, Plenum (1995).
[21] Hohenberg, H. and Kohn, W., Inhomogeneous electron gas, Phys. Rev. 136
B864 (1964).
[22] Kohn, W. and Sham, L. J., Self consistent equations including exchange and
correlation effects, Phys. Rev. 140 A1133 (1965).
[23] Cuevas, Juan Carlos, Introduction to Density Functional Theory, Institut für
Theoretische Festkörperphysik, Universität Karlsruhe, Germany. Tersedia:
www-tfp.physik.uni-karlsruhe.de/~cuevas
[24] Saue, Trond and Helgaker, Trygve, Four-Component Relativistic Kohn-Sham
Theory, Journal of Computational Chemistry Vol. 23 No. 8 (2002) 814-823.
[25] van Wüllen, C., J. Comp. Chem. 20 (1999) 51.
[26] Liu, W. J., Hong, G. Y., Dai, D. D., Li, L. M., Dolg, M., Theor. Chem. Acc.
96 (1997) 75.
[27] Varga, S., Fricke, B., Nakamatsu, H., Mukoyama, T., Anton, J., Geschke, D.,
Heitmann, A., Engel, E., Bastug, T. J., J. Chem. Phys. 112 (2000) 3499.
[28] Yanai, T., Iikura, H., Nakajima, T., Ishikawa, Y., Hirao, K., J. Chem. Phys.
115 (2001) 8267.
[29] Pauling, Linus and Wilson, E. Bright, Jr., Introduction to Quantum
Mechanics, With Applications to Chemistry, Dover Publications, Inc., 31
East 2nd Street, Mineola, N. Y., 11501 (1935).
[30] Atkins, P.W., Molecular Quantum Mechanics, 2nd Edition, Oxford University
Press, UK (1983).
[31] Grant, Guy H. and Richards, W. Graham, Computational Chemistry, Oxford
Science Publications, Oxford University Press, UK (1995).
[32] Heine, Volker, Group Theory in Quantum Mechanics, An Introduction to Its
Present Usage, Pergamon Press, London, UK (1960).
[33] Bishop, David, M., Group Theory and Chemistry, Dover Publications, Inc.,
New York, USA (1973).
[34] United States Department of Commerce, National Bureau of Standards,
Applied Mathematics Series 55. Handbook of Mathematical Functions with
Formulas, Graphs, and Mathematical Tables. Edited by Milton Abramowitz
277
M. Arifin, dkk
[35]
[36]
[37]
[38]
[39]
[40]
[41]
[42]
[43]
[44]
[45]
[46]
[47]
[48]
[49]
278
and Irene A. Stegun. Washington, USA: National Bureau of Standards
(1968).
Slater, John C., Quantum Theory of Atomic Structure, Vol. I dan II, McGrawHill Book Company, Inc., N.Y., USA (1960).
Cowan, Robert D., The theory of atomic structure and spectra, University of
California Press, USA (1981).
Chernysheva, L. V., Cherepkov, N. A. and Radojević, Self-consistent field
Hartree-Fock program for atoms, Computer Physics Communications 11
(1976) 57-73.
Chernysheva, L. V., Cherepkov, N. A. and Radojević, Frozen core HartreeFock program for atomic discrete and continuous states, Computer Physics
Communications 18 (1979) 87-100.
Fischer, C. Froese, Brage, T. and Jönsson, Computational atomic structure,
An MCHF approach, Institute of Physics Publishing, Bristol and Philadelphia
(1997).
Grant, Ian P. and Quiney, Harry M., Foundations of the Relativistic Theory
of Atomic and Molecular Structure, Academic Press (1988).
Dyall, K. G., Grant, I. P., Johnson, C. T. , Parpia, F. A. and Plummer, E. P.,
GRASP: A general-purpose relativistic atomic structure program, Computer
Physics Communications 55 (1989) 425-456.
Edmonds, A. R., Angular Momentum in Quantum Mechanics, Princeton
Landmarks in Physics, Princeton University Press, Third Printing, New
Jersey, USA (1974).
Varshalovich, D. A., Moskalev, A. N., and Khersonskii, V. K., Quantum
Theory of Angular Momentum, World Scientific, Singapore (1988).
Arifin, M., Katō, K. and Myo, T., Notes on 3-Body System, Nuclear Theory
Group, Division of Physics, Graduate School of Science, Hokkaido
University, Sapporo, Japan; (2005).
Fuchs, Martin and Scheffler, Matthias, Ab initio pseudopotentials for
electronic structure calculations of poly-atomic systems using densityfunctional theory, Computer Physics Communications 119 (1999) 67-98.
Gritsenko, Oleg V., van Leeuwen, Robert dan Baerends, Evert Jan, J. Chem.
Phys. 104 (21) (1996) 8535.
Armiento, Rickard, The many-electron energy in density functional theory:
From exchange-correlation functional design to applied electronic structure
calculations, Doctoral Thesis, KTH School of Engineering Sciences,
Stockholm, Sweden (2005).
Tersedia: https://www.ifm.liu.se/theomod/theophys/people/ricar/
ArmientoThesis.pdf
Furnstahl, Dick, Covariant Density Functional Theory, Dept. of Phys. Ohio
State University, September 2004.
Tersedia: http://www.int.washington.edu/talks/WorkShops/
Relative_density_wkshp/People/Furnstahl_R/intcovariant.pdf
Dirac, P. A. M., The principles of quantum mechanics, Fourth edition, The
international series of monographs on physics · 27, Clarendon Press, Oxford,
UK (1958).
Model Thomas Fermi Relativistik Skalar…
[50] Fiolhais, C., Nogueira, F., Marques, M., A Primer in Density Functional
Theory, Springer-Verlag, Berlin, Heidelberg (2003)
Tersedia: http://www.if.pwr.wroc.pl/~scharoch/Abinitio/PrimerDFT.pdf
279