RENCANA PROGRAM DAN KEGIATAN PEMBELAJARAN

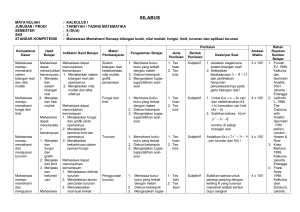
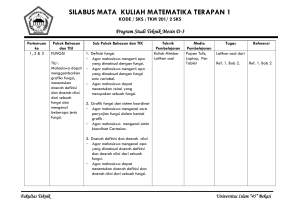
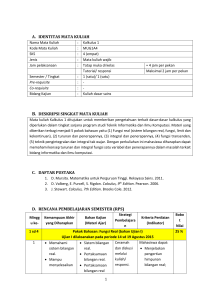
RENCANA PROGRAM DAN KEGIATAN
PEMBELAJARAN SEMESTER (RPKPS)
Mata Kuliah
KALKULUS 1
IF 1106
Oleh :
Dwi Septi Haryani, ST
SEKOLAH TINGGI TEKNOLOGI INDONESIA
TANJUNG PINANG
2010
RENCANA PROGRAM DAN KEGIATAN PEMBELAJARAN SEMESTER (RPKPS)
1. Nama Matakuliah
: KALKULUS 1
2. Kode/SKS
: IF 1106 / 3 sks
3. Semester
: Ganjil
4. Dosen Pembina
: Dwi Septi Haryani, ST
5. Tujuan pembelajaran (kompetensi hardskill):
a. Kompetensi Utama
 Setelah mengikuti perkuliahan , mahasiswa akan dapat menyelesaikan soal-soal
kalkulus yang berhubungan dengan fungsi, limit fungsi, turunan dan integral.

Dapat menyelesaikan masalah terkait dengan turunan, menentukan karakteristik
fungsi berdasarkan turunannya, menentukan nilai ekstrem fungsi kontinyu pada
interval tertutup.

Memahami kaitan dua konsep dasar kalkulus (turunan dan intergral tertentu)
secara tepat.
b. Komptensi Khusus (Hardskill / Softskill)
Setelah mengikuti matakuliah ini mahasiswa diharapkan memiliki
kompetensi secara hardskill dan softskill berikut :
Hardskill
1.
Mahasiswa mampu memahami definisi fungsi, grafik fungsi, daerah definisi,
daerah nilai, bentuk-bentuk fungsi riil, dan beberapa definisi fungsi yang lain.
2.
Mahasiswa dapat memahami fungsi
dalam bentuk
parameter dan bentuk
fungsi dalam koordinat polar
3.
Mahasiswa dapat memahami barisan bilangan, limit barisan, limit tak benarnya,
sifat-sifat limit barisan dan barisan yang istimewa.
4.
Mahasiswa dapat memahami limit fungsi baik limit kiri maupun limit kanan,
sifat-sifat limit fungsi dan asimtot kurva.
5.
Mahasiswa dapat memahami kontinyuitas fungsi.
6.
Mahasiswa dapat memahami definisi turunan, rumus dasar turunan dan mampu
mencari turunan dari ber bagai bentuk fungsi.
7.
Mahasiswa dpt memahami penggunaan Turunan utk menyelesaikan beberapa
persoalan.
Softskill
1. Mampu bekerja sama dalam tim pada saat kerja kelompok
2. Inovatif
3. Aktif (memberi tanggapan, argumen dan pertanyaan)
4. Mandiri
5. Mampu berfikir kritis (koreksi berdasarkan sumber referensi lain)
6. Jumlah jam:
Kegiatan di dalam kelas (3 SKS x 16 minggu) :
a. Kuliah
= 39 sks (13 pertemuan)
b. Ujian tengah semester
= 3 sks
c. Ujian akhir semester
= 3 sks
c. Overview materi
= 3 sks
Total
= 48 sks (16 pertemuan)
Definisi SKS disini adalah 50 menit jam pelajaran. 1 SKS disini mengandung kegiatan
untuk tugas mandiri yang terencana,maka direncanakan pula kegiatan berikut :
Tugas rencana dilar kelas, yaitu dengan rincian sebagai berikut :
1. Tugas mandiri dan kelompok
1 Mencari referensi – referensi dari berbagai sumber
= 3 sks
2 Membuat ringkasan materi berkaitan dengan pokok bahasan
= 3 sks
3 Memecahkan kasus yang diberikan
= 3 sks
4 Tugas individu berupa lembar kerja mahasiswa
= 3 sks
2. Kegiatan Di Kelas
1 Pembahasan Materi
= 21 sks
2 Pembahasan studi kasus
= 12 sks
4 Quis
= 3 sks
Total Jam
= 48 sks
7. Jadwal Kegiatan Mingguan
No
Mg
Kemampuan Akhir
Hard skill
Materi
Soft skill
Model
Pembelajaran
Penugasan
Evaluasi
Indikator
Level
Bobot A
C
P
(%)
1
I
2
II
Mahasiswa dapat :
1. Apresiatif
a. Memahami aturan 2. Responsive
kontrak
perkuliahan
b. Memahami ruang
lingkup mata
kuliah dan
pembagian
waktunya.
c. Dapat
menjelaskan
pengertian dan
aplikasi kalkulus.
Mahasiswa dapat :
1
1. menjelaskan
1.Responsif
pengertian fungsi
2. Aktif
2. menggambarkan
grafik sebuah fungsi
3. menentukan daerah
definisi dan daerah
nilai
4. menjelaskan
pentingnya fungsi
dalam kehidupan
sehari – hari dan
a. Kontrak
perkuliahan,
RPKPS
b. Pengertian dan
aplikasi kalkulus
Fungsi :
a. Definisi (fungsi dan
relasi)
b. Grafik fungsi
c. Daerah definisi dan
daerah nilai
Ceramah
Diskusi
Ceramah
Diskusi
Latihan soal
- Membuat grafik
dari sebuah
fungsi dan
menentukan
daerah hasil dan
daerah
definisnya,
Mampu
mengaplikasikan
teori
kalkulus
dalam
berbagai
ilmu.
5
1,2
1,2
1,2
-Mahasiswa dapat
menyebutkan
definisi fungsi dan
dapat menentukan
relasi yang
merupakan sebuah
fungsi
-Mahasiswa dapat
menggambarkan
sebuah fungsi pada
koordinat cartesian.
-Mahasiswa
dapat
membedakan
dan
10
1,2
2
1,2
matematika.
3
III
Mahasiswa mampu :
a. Menjelaskan jenis –
jenis fungsi, contoh
dan menggambarkan
grafik fungsinya.
1. Aktif
2. Responsif
3. Tanggung
jawab
Fungsi :
a. Fungsi Riil
b. Jenis – jenis fungsi
c. Definisi fungsi yang
lain.
Ceramah 
Diskusi
Latihan soal

Tugas kelompok:
mengkalsifikasik
an jenis – jenis
fungsi dan
memberikan
contoh dari
masing – masing
fungsi dan
menggambarkan
grafik fungsinya.
menuliskan daerah
definisi dan daerah
nilai.
- Mahasiswa dapat
mengenali
dan
memberikan contoh
beberapa fungsi riil
yaitu: fungsi polinom
fungsi aljabar, fungsi
transenden , fungsi
trigonometeri, fungsi
siklometri dan fungsi
hiperbolik
-Mahasiswa dapat
menyebutkan dan
menuliskan
beberapa
fungsi
lain, yaitu : fungsi
konstanta, fungsi
identitas,
fungsi
satu-satu, fungsi
pada,
fungsi
eksplisit,
fungsi
implisit,
fungsi
genap dan fungsi
ganjil.
-Mahasiswa dapat
menentukan
penjumlahan
komponenkomponen vektor.
-Mahasiswa dapat
mengenali
dan
menuliskan
bentuk-bentuk dari
fungsi komposisi,
10
1,2
3
1
1
fungsi
invers,
fungsi
periodik,
fungsi terbatas dan
fungsi monoton.
- Mahasiswa dapat
mencari bentuk
invers
dari
sebuah
fungsi.
Ma- Mahasiswa dapat
menggambarkan
grafik
fungsi
diatas
dalam
koordinat
Cartesian.
4
IV
Mahasiswa memahami
dan menjelaskan fungsi
dalam bentuk parameter
dan dalam koordinat polar.
1.Aktif
2.Kerjasama
3. Responsif
a. Fungsi dalam bentuk
parameter
b. Fungsi dalam
koordinat polar
Ceramah
Diskusi
Latihan soal
- Mengubah
fungsi dari
bentuk
umum ke
bentuk
parameter.
- Mengubah
fungsi dalam
koordinat
cartesian ke
fungsidalam
koordinat
polar dan
sebaliknya.
-
-
-
-
Mahasiswa
mampu
mengenali fungsi
dalam
bentuk
parameter.
Mahasiswa dapat
mengubah sebuah
fungsi
dari
bentuk parameter
kedalam
bentuk biasa.
Mahasiswa
mampu
mengubah bentuk
sebuah
fungsi
dari bentuk polar
kedalam
bentuk cartesian
dan sebaliknya.
Mahasiswa
mampu
10
1,2
1,2
1,2
5
V
Mahasiswa mampu :
Menjelaskan tentang
barisan bilangan dan limit
barisan
1. Aktif
2. Kerjasama
3.Responsif
a.
b.
c.
d.
Barisan bilangan
Limit barisan
Limit tak sebenarnya
Sifat – sifat limit
barisan
e. Barisan yang
istimewa
Ceramah
Diskusi
Latihan soal
 Menentukan

suku umum dari

sebuah barisan
bilangan
 Dapat
menentukan
limit sebuah

barisan dan
memeriksa
barisan yang

konvergen.



menggambarkan
sebuah
fungsi
dalam koordinat
polar.
Memahami
barisan bilangan.
Mampu
menentukan suku
umum
dari
sebuah
barisan
bilangan.
Dapat
menentukan limit
sebuah barisan.
Dapat memeriksa
barisan
yang
konvergen
dan
barisan
yang
divergen, dengan
menggunakan
limit.
Mengenal
apa
yang
disebut
dengan limit tak
sebenarnya.
Memahami sifatsifat limit barisan
dan
dapat
memanfaatkan
sifat-sifat tersebut
untuk
menentukan limit
sebuah barisan.
Mengenal
beberapa barisan
istimewa dan
limit dari barisanbarisan tersebut
10
1,2
1,2
2,3
6
7
VI
VII
Mahasiswa mampu :
Menjelaskan tentang limit
fungsi.
Mahasiswa mampu :
a. Menjelaskan tentang
fungsi yang kontinyu
dan diskontinyuitas
1. Aktif
2. Kerjasama
3.Responsif
1. Aktif
2. Kerjasama
3.Responsif
a. Limit fungsi
b. Limit kiri dan limit
kanan
c. Sifat – sifat limit
fungsi
d. Menentukan asimptot
dengan limit
a. Definisi fungsi yang
kontinyu
b. Diskontinyuitas
c. Limit dari fungsi –
fungsi istimewa
Ceramah
Diskusi
Latihan soal
Ceramah
Diskusi
Latihan soal
 Menentukan
limit suatu
fungsi dengan
berbagai
metode.
 Menentukan
limit kiri dan
kanan
 Memahami
dan
dapat menentukan
limit sebuah fungsi
 Memahami
apa
yang
dimaksud
dengan limit kiri
dan limit kanan
sebuah fungsi.
 Mengenal
dan
mengerti sifat limit
fungsi.
 Dapat
menggunakan sifatsifat limit fungsi
untuk menentukan
limit sebuah fungsi.
 Mampu
menentukan limit
sebuah fungsi pada
sebuah titik.
 Mahasiswa dapat
menggunakan limit
untuk
mencari
asimptot
suatu
kurva.
 Mengerti
apa
yang
dimaksud
dengan
kontinyuitas fungsi.
 Dapat
menyelidiki
kontinyuitas
sebuah fungsi.
 Mampu
menentukan titik
diskontinuitas
sebuah fungsi.
 Mengenal
10
1,2
1,2
2,3
5
1,3
1,3
1,3
beberapa
limit
fungsi istimewa.
8
VIII
9
IX
Ujian Tengah Semester
Mahasiswa mampu :
menjelaskan tentang
turunan sebuah fungsi
1. Aktif
2. Kerjasama
3.Responsif
a. Definisi turunan
b. Rumus dasar
turunan
Ceramah
Diskusi
 Mancari
turunan dari
sebuah fungsi
Latihan soal
10
X
Mahasiswa mampu :
menjelaskan aturan rantai
untuk fungsi tersusun dan
turunan dari fungsi invers
1.Responsif
2.Aktif
3.Kerjasama
a. Aturan rantai untuk
fungsi tersusun
b. Turunan dari fungsi
invers
Ceramah
Diskusi
Latihan soal
 Mencari
turunan dari
fungsi invers
 Mengerti
akan
turunan
(derivative).
 Mampu
menggunakan
limit
untuk
mencari turunan
sebuah fungsi.
 Mampu
menyelidiki
apakah sebuah
fungsi
mempunyai
turunan
pada
sebuah titik.
Mengenal
rumus-rumus
dasar
turunan
dan
dapat
memanfaatkanny
a
untuk
menentukan
turunan berbagai
fungsi.
 Mengenal fungsi
tersusun.
 Mampu
menentukan
turunan
dari
sebuah
fungsi
tersusun..
Mampu
menentukan
turunan
dari
fungsi invers
5
1,3
1,3
1,3
10
2,3
1,3
1,3
11
12
13
XI
XII
Mahasiswa mampu :
menjelaskan mencari
turunan dari fungsi
implisit dan dengan batuan
logaritma
1.Aktif
2.Responsif
3 Disiplin
Mahasiswa mampu :
Menjelaskan turunan dari
fungsi dalam persamaan
parameter dan
menjelaskan tentang
turunan kedua dan turunan
yang ebih tinggi
1.responsif
2. Inisiatif
3.Aktif
XIII Mahasiswa mampu :
a. Menggunakan turunan
untuk mencari garis
singgung dan garis
normal, Panjang garis
a. Turunan dari fungsi
implisit
b. Penurunan dengan
batuan logaritma
Ceramah
Diskusi
Latihan soal
1.responsif
2. Inisiatif
3.Aktif
a. Turunan dari fungsi
dalam persamaan
parameter
b. Turunan kedua dan
turunan lebih tinggi
b. Garis singgung dan
garis normal
c. Panjang garis
singgung dan garis
normal
Ceramah
Diskusi
Latihan soal
Ceramah
Diskusi
Latihan soal
 Menentukan
turunan dari
fungsi implisit.
 Menentukan
turunan dengan
bantuan
logaritma
 Mencari
turunan dari
fungsi
persamaan
parameter
 Menentukan
turunan kedua
dan turunan
lebih tinggi dari
sebuah fungsi
 Dapat
menentukan
turunan
dari
sebuah fungsi
implisit
 Dapat mencari
turunan sebuah
fungsi dengan
bantuan
logaritma
 Mampu
menentukan
turunan sebuah
fungsi dalam
persamaan
parameter
 Mengerti cara
menentukan
turunan kedua
dan turunan yang
lebih tinggi dari
sebuah fungsi
Dapat
menentukan
turunan
kedua/lebih
tinggi
dari
sebuah
fungsi
implisit
fungsi
tersusun
dan
fungsi
dalam
persamaan
parameter
Mahasiswa mampu
menggunakan
turunan
untuk
mencari :
 persamaan garis
5
1
2
3
8
1,2
1,2
1,2
3
,3
3
singgung dan garis
normal, Panjang sub
normal dan sub tangen
14
XIV Mahsiswa mampu :
Meenggunakan turunan
untuk mencari sudut
perpotongan antar dua
kurva dan menentukan titik
nilai ekstrem suatu fungsi.
d. Panjang sub normal
dan sub tangen
1.responsif
2. Inisiatif
3.Aktif
a. Sudut perpotongan
antar dua kurva
b. Maksima dan minima
c. Bentuk tak tentu dan
aturan L’Hospital
pada limit.
Ceramah
Diskusi
Latihan soal
singgung
dan
garis normal dari
sebuah
kurva
pada suatu titik
yang diketahui.
 panjang
garis
singgung
dan
garis normal.
Panjang
sub
normal
dan
subtangen
- Mencari sudut
Mahasiswa mampu
perpotongan antar menggunakan
dua kurva.
turunan untuk :
-Mencari
dan
- Mencari nilai
menunjukkan
ekstrem sebuah
besar
sudut
fungsi
perpotongan antara
2 kurva
yang
diketahui.
- Memeriksa sebuah
fungsi apakah
fungsi naik atau
fungsi
turun,
fungsi
cembung
/cekung
-Mencari
dan
menentukan
titik/nilai
Ekstrim
suatu
fungsi.
- mengenali
limit
dengan
bentuk
taktentu
-menggunakan
turunan
untuk
mencari nilai suatu
limit
(aturan
15
16
XV
XVI
Mahasiswa mampu :
Menggunakan turunan
untuk menentukan
kelengkungan kurva dan
mengukur besarnya
kecepatan percepatan
benda.
1.responsif
2. Inisiatif
3.Aktif
a. kelengkungan
b. kecepatan dan
percepatan
Ceramah
Diskusi
Latihan soal
Ujian Akhir Semester
- Mencari
kelengkungan
sebuah kurva
- Mencari
besarnya
kecepatan dan
percepatan
benda dengan
turunan.
L’Hospital)
Mahasiswa mampu
menggunakan
turunan untuk :
- menentukan
kelengkungan
kurva pada suatu
titik.
- menentukan
besarnya
laju
perubahan dari
kelengkungan
suatu kurva, dan
menentukan
lingkaran
kelengkungan
- Mahasiswa
mampu
menggunakan
turunan
untuk
mencari besarnya
kecepatan
dan
percepatan suatu
partikel/benda
yang
bergerak
dalam lintasan
garis lurus.
8. Topik Bahasan
Kegiatan di luar kelas (pengerjaan tugas kelompok dan individu) dilaksanakan
dengan waktu yang lebih bebas, namun tetap dalam jadwal mingguan yang telah
ditetapkan. Materi perkuliahan yang dibahas diwujudkan dalam bentuk presentasi
(microsoft power point) untuk active learning, yang tersusun berdasarkan topik
sebagai berikut:
Materi
1
Fungsi
Topik
2
Fungsi
3
Fungsi
4.
Barisan Bilangan
5
Limit Fungsi
6
Kontiyuitas Fungsi
7
Turunan
8
Turunan
9
Turunan
10
Turunan
11
Aplikasi turunan
a.
b.
c.
a.
b.
c.
a.
b.
a.
b.
c.
d.
e.
a.
b.
c.
d.
a.
b.
c.
a.
b.
a.
b.
a.
b.
a.
b.
Rincian Isi Materi
Definisi fungsi
Grafik fungsi
Daerah definisi dan daerah nilai
Fungsi Riil
Beberapa Jenis Fungsi
Beberapa definisi fungsi yang lain
Fungsi dalam bentuk parameter
Fungsi dalamkoordinat polar
Barisan bilangan
Limit barisan
Limit tak sebenarnya
Sifat – sifat limit barisan
Barisan yang istimewa
Limit fungsi
Limit kiri dan limit kanan
Sifat - sifat limit fungsi
Menentukan asimptot dengan limit
Definisi fungsi yang kontinyu
Diskontinyuitas
Limit dari fungsi – fungsi istimewa
Definisi turunan
Rumus dasar turunan
Aturan rantai untuk fungsi tersusun
Turunan dari fungsi invers
Turunan dari fungsi implisit
Penurunan dengan bantuan logaritma
Turunan fungsi dalam bentuk parameter
Turunan kedua dan turunan yang lebih
tinggi
a. Garis singgung
b. Garis normal
c. Panjang garis singgung
d. Panjang garis normal
e. Panjang sub normal
f. Panjang sub tangen
12
Aplikasi turunan
13
Aplikasi turunan
14
Aplikasi turunan
a.
b.
a.
b.
a.
Sudut perpotongan antara dua kurva
Maksima dan minima
Kelengkungan
Kecepatan dan percepatan
Bentuk tak tentu dan aturan L”Hospital
9. Pemberian Tugas
Deskripsi Tugas
Mahasiswa diminta aktif untuk mencari bahan tambahan sendiri untuk setiap materi
melalui Internet. Tugas terdiri atas tugas individual dan kelompok. Adapun rincian tugas
adalah sebagai berikut:
Tugas kelompok:
Tugas ini adalah yang dikerjakan oleh kelompok yang terdiri dari 4-5 orang yang
membahas materi pelajaran dan mengerjakan soal (study kasus). Tugas ini dimaksudkan
untuk memfasilitasi mahasiswa yang lemah melalui tutor teman sebaya. Penilaian dilihat
dari segi kekompakan, pemerataan tugas, penguasaan materi dan kedisiplinan kelompok,
diberi bobot 20 %.
Tugas individual :
Lembar kerja dirancang secara hati-hati dengan memperhatikan tujuan pemelajaran,
pemelajar, dan metode yang diterapkan. Lembar kerja menjadi bagian terintegrasi dari
pemelajaran, bukan sekedar lembar latihan saja. Lembar kerja dapat berfungsi sebagai
sarana untuk membangkitkan kembali pengetahuan dasar yang diperlukan, orientasi,
latihan, dan umpan balik
Tugas ini dikerjakan secara individu, yaitu berupa :
1. Mengerjakan soal secara manual di lembar kerja mahasiswa yang sudah
disediakan.
2. Membuat rangkuman dari materi yang bersangkutan.
3. Essay
10. Penilaian
Diskripsi Ujian :
Soal pada ujian tengah semester dan akhir semester merupakan soal yang berbentuk
1.
Extended response essay (menentukan, menerapkan, memilih atau menilai
prosedur – prosedur penyelesaian, memberi argumentasi). Jumlah soal 2 dengan
bobot 50%
2. Restricted response essay (menghitung, menginterpretasikan, mengidentifikasi
dan mengklasifikasi). Jumlah soal 2 dengan bobot 30%
3. Pilihan ganda (menganalisa, menilai dan memilih). Jumlah soal 5 dengan bobot
20%.
Penilaian individual 80 %, meliputi:
1. Harian :
10 %:
- Partisipasi
- Kerja keras
- Percaya diri
2. Quiz
: 25 %
3. Semester
: 20 %
4. Tugas
: 25 %
Penilaian kelompok
10 %, meliputi:
- Kekompakan
- Pemerataan tugas
- Penguasaan materi , dan
- Kedisiplinan kelompok
Standar konversi nilai yang direncanakan:
A
B
C
D
E
> 85
70 - 85
60 - 70
45 - 60
< 45
11.
Referensi :
1.
Yusuf Yahya, D. Suryadi H.S., Agus S., Matematika Dasar untuk Perguruan
Tinggi, Ghalia Indonesia, Jakarta, 1995
2.
Edwin J. Purcell, Dale Varberg, Kalkulus dan Geometri Analitis, jilid 1,
terjemahan : I Njoman Susila, Bana Kartasasmita, Rawuh, Erlangga, Jakarta,
1995.
12. Perencanaan Monitoring dan Umpan Balik
Rencana dokumen monitoring dan umpan balik meliputi dan diwujudkan dalam
bentuk form-form yang terdiri atas: rencana dokumen/form kegiatan mingguan,
Rencana dokumen/form, umpan balik dari mahasiswa, dan rencana dokumen/form
perubahan.
No
1
2
3
b. FORMAT KEGIATAN MINGGUAN
Nama
Individual
Kelompok
mahasiswa
Hr/PBM
Mid smstr Tgs kmpk merata penguasaan
Pts Kk Pd
A
B
Dst
Ket
Ds
FORMAT UMPAN BALIK DARI MAHASISWA
Apa yang anda dapatkan dalam perkuliahan hari ini?
Apa kesulitan anda hari ini?
Apa yang anda sukai dalam kuliah hari ini?
Apa yang tidak anda sukai dalam kuliah hari ini?
Masalah yang bersifat umum segera diperbaiki dan langsung diterapkan pada
pertemuan berikutnya, sedangkan yang sifatnya mendasar akan dicatat untuk perbaikan pada
semester berikutnya.Perencanaan Evaluasi adalah sebagai berikut:
c. FORMAT PERUBAHAN
GAP
AKAR MASALAH
ALTERNATIF SOLUSI
Evaluasi meliputi:
1. Hasil pembelajaran
Evaluasi kemampuan mahasiswa dalam memahami konsep dilakukan secara tertulis
sebanyak 2 kali, yaitu ujian tengah semester dan ujian akhir semester. Hasil ini
menggambarkan kemampuan individual mahasiswa dalam mencapai target kompetensi yang
berhubungan dengan kemampuan pemahaman terhadap materi perkuliahan yang diberikan.
Sehingga dapat dianalisis persentase mahasiswa yang berhasil mencapai target kompetensi
tersebut.Evaluasi terhadap kemampuan praktis mahasiswa dilakukan pada setiap kali
pembahasan materi yang berhubungan dengan praktek tersebut.
2. Proses pembelajaran
Proses pembelajaran dievaluasi dengan menganalisis monitoring form dan umpan balik
seperti contoh di atas, untuk melihat keefektifan dari setiap komponen pembelajaran.
Hambatan dan kekurangan
a. Terkadang mahasiswa telat mengisi KRS, sehingga jumlah sks yang dicapai tidak
maksimum
b. Bagi mahasiswa yang sudah bekerja, waktu belajar lebih banyak tersita oleh kerja
c. Terkadang jadwal kerja dinas membuat mahasiswa harus meninggalkan kuliahnya
sementara.
Kemungkinan perbaikan
a. Diberikan tugas tambahan
b. Diberikan ujian perbaikan
c. Diberikan waktu khusus untuk diskusi dengan dosen diluar jam mata kuliah