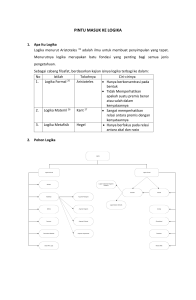
representasi pengetahuan

REPRESENTASI
PENGETAHUAN
Pengertian Representasi Pengetahuan
• Dalam menyelesaikan masalah tentu membutuhkan
pengetahuan-pengetahuan yang cukup. Selain itu,
sistem harus bisa menalar.
• Oleh karena itu, representasi pengetahuan dan
kemampuan untuk melakukan penalaran dalam
kecerdasan buatan adalah hal yang sangat penting.
• Meskipun sistem memiliki banyak pengetahuan tapi tidak
bisa melakukan penalaran, maka hal itu percuma saja.
• Sebaliknya jika sistem memiliki kemampuan untuk
menalar namun pengetahuan yang dimiliki tidak
memadai, maka hasil yang diperoleh menjadi tidak
maksimal.
• Banyak cara untuk menyatakan representasi pengetahuan dan
setiap cara mempunyai kelebihan dan kelemahan masing-masing
• Beberapa cara atau teknik representasi pengetahuan antara lain :
– Logika
– Frame
– Schema
– Jaringan Semantik
– Kaidah produksi (Production rules)
– List, digunakan pada LISP
– Tree, untuk heuristic search
– dan lain-lain
• Karakteristik RP:
– Dapat diprogramkan
– Dapat dimanfaatkan untuk penalaran, menggambarkan
kesimpulan sebagai fungsi kecerdasan
• Dalam representasi pengetahuan, ada dua hal yang
harus diperhatikan, yakni :
1. Fakta
Fakta adalah objek yang direpresentasikan. Ini
menerangkan tentang benda yang ada dalam domain
masalah. Fakta dapat berupa keterangan atau kalimat
dalam bahasa alami, logika atau benda.
2. Formula
yakni bentuk representasi yang dapat dimanipulasi
dalam proses pemecahan soal. Bentuk ini harus dapat
menggambarkan hubungan antar komponen domain
masalah.
PENGETAHUAN
= data/fakta +
mekanisme
penalaran
Fakta, ide, teori,
hubungannya dalam domain
tertentu
Mekanisme
Penalaran
KNOWLEDGE BASE
INFERENCE MECHANISM
Kumpulan prosedur yang
digunakan untuk menguji
(melacak dan mencocokkan)
untuk mencari solusi
Langkah membangun sistem AI
Pengumpulan
pengetahuan dari
berbagai sumber
Otak/pengetahua
n pakar
Buku
Artikel
dll
Di Organisasikan
diKodifikasi
(Skema)
Skema “DEKLARATIF”
Skema “PROSEDURAL”
Cocok untuk menggambarkan faktafakta asersi
-
Cocok untuk menyatakan aksi
dan prosedur
Yang termasuk skema representasi
pengetahuan deklaratif:
-
Yang termasuk skema
representasi pengetahuan
deklaratif:
1. LOGIKA
2. JARINGAN SEMANTIK
1. PROSEDUR / SUBROUTINE
3. FRAME
2. KAIDAH PRODUKSI
4. SCRIPT
Alasan Pemilihan
• Why knowledge representation rather
than information representation?
– Karena pada konvensional database
merepresentasikan data secara sederhana:
string, number, boolean
– Namun KB menganggap pengetahuan lebih
kompleks, seperti proses, prosedur, aksi,
waktu, tujuan dan penalaran
– Knowledge should be collected, codified,
and organized in systematic order
1. LOGIKA
• Logika merupakan suatu pengkajian ilmiah tentang
serangkaian penalaran, sistem kaidah dan prosedur
yang membantu proses penalaran
• Proses Logika : Proses membentuk kesimpulan atau
menarik suatu inferensi berdasarkan fakta yang telah
ada
• Merupakan bentuk representasi pengetahuan yang
paling tua
• Bentuk logika ada 2 macam : Logika Proposisi dan
Logika Predikat
OUTPUT :
INPUT :
Premis atau Fakta
PROSES LOGIKA
Inferensi atau
konklusi
PENALARAN DEDUKTIF
• Penalaran ini bergerak dari penalaran umum menuju ke
konklusi khusus
• Umumnya dimulai dari suatu sylogisme, atau pernyataan
premis dan inferensi
• Umumnya terdiri dari 3 bagian: premis mayor, premis
minor dan konklusi.
• Contoh
Premis mayor : Jika hujan turun saya tidak akan lari pagi
Premis Minor : Pagi ini hujan turun
Konklusi : Oleh karena itu pagi ini saya tidak akan lari
pagi
PENALARAN INDUKTIF
• Dimulai dari masalah khusus menuju ke masalah umum
• Menggunakan sejumlah fakta atau premis untuk menarik
kesimpulan umum.
• Contoh:
Premis : Dioda yang salah menyebabkan peralatan elektronik rusak
Premis : Transistor rusak menyebabkan elektronik rusak
Premis : IC rusak menyebabkan peralatan elektronik tidak berfungsi
Konklusi : Maka, peralatan semi konduktor rusak merupakan penyebab
utama rusaknya peralatan elektronik
• Konklusi tidak selalu mutlak, dapat berubah jika
ditemukan fakta-fakta baru
LOGIKA PROPOSISI
Resolusi dalam Logika Proposisi
• Inferensi pada logika proposisi dapat dilakukan
dengan menggunakan resolusi.
• RESOLUSI adalah suatu aturan untuk melakukan
inferensi yg dapat berjalan secara efisien dalam
suatu bentuk khusus yg disebut
Conjunctive
Normal Form (CNF).
• CNF ini memiliki ciri-ciri sebagai berikut :
– Setiap kalimat merupakan disjungsi literal
– Semua kalimat terkonjungsi secara implisit
LOGIKA PROPOSISI
 Dua atau lebih proposisi dapat digabungkan dengan
menggunakan operator logika :
a. Negasi
b. Konjungsi
c. Disjungsi
d. Implikasi
e. Ekuivalen
:  (NOT)
:  (AND)
:  (OR)
:  (IF-THEN)
:
 Operator NOT
: digunakan untuk memberikan nilai
negasi (lawan) dari pernyataan yang telah ada.
LOGIKA PROPOSISI
Resolusi dalam Logika Proposisi
• Langkah-langkah mengubah kalimat ke dalam bentuk CNF,
sebagai berikut :
> hilangkan implikasi dan ekuivalensi
mis. X  Y menjadi X  Y (hukum implikasi)
X  Y menjadi (X=>Y)  (Y=>X) (hukum bi-implikasi)
(X  Y)(Y  X) (hukum implikasi)
> kurangi lingkup semua negasi menjadi satu negasi saja
mis. ( X) menjadi X (hukum negasi ganda)
(X  Y) menjadi (X  Y) (hukum de’Morgan)
(X  Y) menjadi (X  Y) (hukum de’Morgan)
> gunakan aturan assosiatif dan distributif untuk
mengkonversi menjadi conjunction of disjunction
mis. Assosiatif : (A  B)  C = A  (B  C)
Distributif : (A  B)  C = (A  C)  (B  C)
LOGIKA PROPOSISI
Resolusi dalam Logika Proposisi
• Algoritma Resolusi
Input
: serangkaian clauses yang disebut axioma dan
tujuannya.
Output :uji apakah tujuan diturunkan dari axioma
Begin
1. Kembangkan serangkaian pernyataan axioma termasuk tujuan
yang dinegasikan
2. Representasikan tiap elemen statemen ke dalam Conjunctive
Normal Form (CNF)
berdasarkan langkah-langkah berikut :
- Hilangkan operator “if-then” dengan operasi NEGATION dan OR
berdasarkan hukum logika
LOGIKA PROPOSISI
Resolusi dalam Logika Proposisi
• Algoritma Resolusi
Input : serangkaian clauses yang disebut axioma dan tujuannya.
Output :uji apakah tujuan diturunkan dari axioma
3. Repeat
a. Pilih dua clauses mana saja dari S, sehingga satu clause berisi
literal yang dinegasikan dan clause yang lainnya berisi literal
positif yang berhubungan (literal yang tidak dinegasikan)
b. Pisahkan dua clauses ini dan panggil clause yang dihasilkan
(resolvent). Hapus parent clause dari S.
Until sebuah clause null dihasilkan atau tidak ada progress lebih
lanjut yang bisa dibuat
4. Jika sebuah clause null dihasilkan, maka “tujuan terbukti” atau
Pernyataan “valid”
LOGIKA PROPOSISI
Resolusi dalam Logika Proposisi
Contoh 1 :
Diketahui sejumlah basis pengetahuan berikut ini :
a. Kelembaban tinggi atau langit mendung
b. Jika langit mendung maka hari akan hujan
c. Jika kelembaban tinggi maka hari panas
d. Hari tidak panas
dan tujuannya atau kesimpulannya adalah hari akan hujan.
Buktikanlah berdasarkan teorema resolusi bahwa tujuan
atau kesimpulan adalah diturunkan dari basis pengetahuan.
LOGIKA PROPOSISI
Resolusi dalam Logika Proposisi
Penyelesaian :
1. Pertama-tama buatkan variabel clauses di atas dengan simbol-simbol
p, q, r dan s.
p = kelembaban tinggi
q = langit mendung
r = Hari akan hujan
s = Hari panas
2. Buatkan ekspresi logikanya berdasarkan basis pengetahuan yang
dibangun sebagai berikut :
1. p V q
2. q  r
3. p  s
4. ¬ s
Tujuan yang hendak dibuktikan adalah r
LOGIKA PROPOSISI
Resolusi dalam Logika Proposisi
Penyelesaian :
3. Ubah proposisi yang mengandung implikasi ke dalam bentuk normal
konjungtif (CNF) yang diperoleh dari clauses di atas sebagai berikut :
1. p V q
2. ¬ p V s
3. ¬ q V r
4. ¬ s
dan ditambahkan dengan tujuan yang dinegasikan yakni ¬r. Sehingga
rangkaian S kini menjadi 5 clauses, yakni :
1. p V q
2. ¬ p V s
3. ¬ q V r
4. ¬ s
5. ¬r
LOGIKA PROPOSISI
Resolusi dalam Logika Proposisi
Penyelesaian :
4. Berdasarkan algoritma resolusi, buatkan
pohon resolusi (graf resolusi) untuk
membuktikan tujuan/kesimpulan tersebut
sebagai berikut :
LOGIKA PROPOSISI
pVq
¬q V r
pVr
¬p V s
rVs
¬s
r
¬r
ǿ
Pohon resolusi untuk membuktikan bahwa hari akan hujan.
Kesimpulan : Karena resolusi berakhir dengan clause null, maka
tujuan/kesimpulan adalah terbukti (valid).
LOGIKA PROPOSISI
Contoh 2.
Diketahui sejumlah basis pengetahuan sebagai berikut :
1. Budi anak yang baik
2. Jika budi anak yang baik dan budi senang bantu orang
tua, maka budi akan menjadi orang sukses
3. Jika Budi Badannya sehat atau budi istirahatnya cukup,
maka Budi senang bantu orang tua
4. Budi istirahatnya cukup
Buktikan kebenarannya bahwa “Budi akan menjadi orang
sukses”!
LOGIKA PROPOSISI
Contoh 2.
Penyelesaian :
1. Pertama-tama buatkan variabel clauses di atas dengan simbol-simbol p,
q, r dan s.
p = Budi anak yang baik
q = Budi senang bantu orang tua
r = Budi akan menjadi orang sukses
s = Budi badannya sehat
t = Budi istirahatnya cukup
2. Buatkan ekspresi logikanya berdasarkan basis pengetahuan yang
dibangun sebagai berikut :
1. p
2. (p  q) r
3. (s  t)  q
4. t
Tujuan yang hendak dibuktikan kebenarannya adalah r
LOGIKA PROPOSISI
Resolusi dalam Logika Proposisi
Penyelesaian :
3. Ubah proposisi yang mengandung implikasi ke dalam bentuk normal konjungtif
(CNF) yang diperoleh dari clauses di atas sebagai berikut :
1. p
2. ¬ p V ¬ q V r  Budi anak yang baik atau Budi tak senang bantu ortu
atau Budi akan menjadi orang sukses
3. ¬ s V q
 Budi badannya tak sehat atau Budi senang bantu ortu
4. ¬ t V q
 Budi tidak cukup istirahat atau Budi senang bantu ortu
5. t
dan ditambahkan dengan tujuan yang dinegasikan yakni ¬r. Sehingga
rangkaian proposisi S kini menjadi 6 clauses, yakni :
1. p
2. ¬ p V ¬ q V r
3. ¬ s V q
4. ¬ t V q
5. t
6. ¬r
LOGIKA PROPOSISI
¬ pV¬ qVr
r
p
¬ p V ¬q
¬q
¬ tVq
¬t
t
ǿ
Pohon resolusi untuk membuktikan bahwa Budi akan
menjadi orang sukses
Kesimpulan : Karena resolusi berakhir dengan clause
null, maka tujuan/kesimpulan adalah terbukti (valid).
LOGIKA PROPOSISI
Contoh 2.
Diketahui sejumlah basis pengetahuan sebagai berikut :
1. Jika pejabat melakukan korupsi maka rakyat tak akan
marah atau kejaksaan akan memeriksanya
2. Jika kejaksaan tidak memeriksanya, maka rakyat akan
marah
3. Kejaksaaan memeriksanya
4. Pejabat tidak melakukan korupsi
Buktikan kebenarannya bahwa “pejabat tidak melakukan
korupsi”!