BAB 3 - BLOGdetik

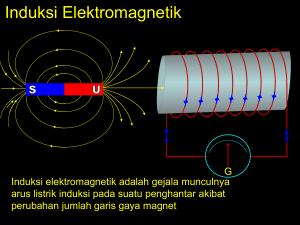
DAFTAR ISI
DAFTAR ISI..............................................................................1
BAB 21. INDUKSI ELEKTROMAGNETIK ................................2
21.1 Hukum Faraday dan Lenz...........................................2
21.2 Generator Listrik .........................................................6
21.3 Transformator .............................................................7
21.4 Indukstansi ..................................................................9
21.5 Energi dalam Medan Magnet ....................................12
21.6 Rangkaian Listrik AC ................................................14
21.7 Osilator......................................................................21
21.8 Quis 21......................................................................21
1
BAB 21. INDUKSI ELEKTROMAGNETIK
21.1 Hukum Faraday dan Lenz
v
Hukum induksi Faraday menyatakan bahwa gaya gerak listrik (ggl) induksi ε di dalam sebuah
rangkaian adalah sama (kecuali tanda negatifnya) dengan kecepatan perubahan fluks yang melalui
rangkaian tersebut, atau dalam bentuk persamaan
v
dΦ
ε =−
dt
v
(1)
Tanda negatif pada hukum induksi Faraday berarti bahwa ggl induksi yang timbul akan
menyebabkan arus yang melawan penyebab timbulnya ggl induksi itu sendiri. Pernyataan ini dikenal
sebagai hukum Lenz. Hukum ini direduksi dari prinsip kekekalan energi oleh H.F. Lenz pada tahun
1834. Sebagai gambaran dari hukum Lenz ini, perhatikan Gambar 1 berikut. Arah arus pada gambar
tersebut dapat kita tentukan dengan menggunakan hukum Lenz
Gambar 1
Bila magnet digerakkan ke bawah, fluks induksi yang menembus simpal kawat berkurang.
Menurut hukum Lenz, arah arus induksi haruslah melawan penyebabnya, yaitu melawan
berkurangnya fluks dengan memperkuat fluks yang sudah ada. Jadi medan magnet yang dihasilkan
kawat harus berarah ke atas sehingga arah arus mengarah ke kanan.
Tinjaulah Gambar 2 yang memperlihatkan sebuah simpal kawat segiempat siku-siku yang
v
lebarnya l, dengan salah satu ujungnya berada dalam medan magnet uniform B . Simpal tersebut
ditarik ke kanan dengan laju konstan v. Anggap bahwa batas medan magnet diberikan oleh garis
putus-putus, di luar garis tersebut medan magnet sama dengan nol.
2
Gambar 2
Fluks Φ yang tercakup oleh simpal adalah
Φ = Blx = BA
(2)
di mana lx adalah luas bagian simpal yang berada di dalam medan magnet. Dari hukum
Faraday, didapatkan ggl induksi
ε =−
dΦ
d
dx
= − ( Blx ) = − Bl
= − Blv
dt
dt
dt
(3)
Dari hukum Lenz, arus tersebut (dengan demikian ε) harus searah dengan arah perputaran
jarum jam. Arah tersebut menentang perubahan (pengurangan) Φ dengan menghasilkan sebuah
medan yang searah dengan medan luar di dalam simpal tersebut. Dengan kata lain harga ε positif jika
arus yang terjadi menghasilkan induksi magnet yang searah dengan induksi magnet luar yang sudah
ada. Jadi karena ε positif maka arus yang timbul adalah
i=
ε
R
=
Blv
R
(4)
dengan R adalah hambatan simpal.
Untuk menghasilkan arus ini, sumber ggl harus menstransfer energi ke dalam rangkaian
sebesar
P = εi =
ε2
R
=
B 2l 2 v 2
R
(5)
v v
v
Arus di dalam simpal menimbulkan gaya-gaya F1 , F2 dan F3 yang bekerja pada ketiga
penghantar tersebut menurut persamaan
v v v
F = il x B
(6)
3
v
v
Karena F2 dan F3 mempunyai besar sama dan arah berlawanan maka kedua gaya tersebut
saling meniadakan. Satu-satunya gaya yang menentang usaha kita untuk menggerakkan simpal
v
adalah F1 yang besarnya
F1 = ilB sin 90° =
B 2l 2 v
R
(7)
Daya yang ditimbulkan oleh gaya tersebut
PF = F1v =
B 2l 2 v 2
R
(8)
yang identik dengan persamaan (5).
Dengan prinsip kekekalan kekekalan energi maka energi termal harus muncul dalam hambatan
dengan kecepatan yang sama. Dengan mengingat persamaan (4) maka kita dapat menyatakan
kecepatan produksi energi termal PT
2
B 2l 2 v 2
⎛ Blv ⎞
PT = i R = ⎜
⎟ R=
R
⎝ R ⎠
2
(9)
yang juga identik dengan persamaan (5).
Kemiripan bentuk dalam persamaan (5), (8) dan (9) menyatakan bahwa daya yang kita berikan
untuk menarik simpal sama dengan daya yang digunakan untuk menghasilkan arus yang pada
akhirnya diubah menjadi energi termal, yang sesuai dengan hukum kekekalan energi. Dengan kata
lain, persamaan di atas merupakan ilustrasi kuantitatif mengenai terjadinya perubahan energi mekanis
menjadi energi listrik yang kemudian diubah menjadi energi termal.
Kita tinjau sekali lagi berlakunya hukum Lenz pada persoalan di atas. Penyebab timbulnya ggl
induksi dapat ditinjau dari dua sisi : pertama, Penyebab ggl induksi karena simpal digerakkan ke
kanan. Arus yang timbul menyebabkan pada simpal bekerja gaya resultan yang berarah ke kiri, yaitu
melawan penyebabnya. Kedua, Penyebab timbulnya ggl induksi karena perubahan fluks induksi,
untuk kasus di atas fluks berkurang. Akibatnya arus yang timbul mempunyai arah memperkuat fluks
induksi, jadi melawan berkurangnya fluks induksi
Contoh 1
Dua buah kumparan dililitkan pada karton. Kumparan 1 dihubungkan dengan sumber tegangan
dan hambatan geser seperti terlihat pada Gambar 3. Jika penggeser pada R1 digeser ke kiri, yang
4
berarti arus bertambah, maka pada kumparan 2 akan terjadi arus induksi. Ke manakah arah arus
pada R2.
Gambar 3
Jawab
v
Dengan bertambahnya arus pada kumparan 1 maka induksi magnet B1 yang berarah ke kanan
akan bertambah. Karena fluks berubah dengan waktu maka pada kumparan 2 akan timbul arus
induksi. Menurut hukum Lenz arah arus harus melawan penyebabnya yaitu bertambahnya fluks. Agar
v
ini terjadi maka arus pada kumparan 2 harus menghasilkan medan magnet arah ke kiri yaitu B2 .
Dengan demikian arah arus pada kumparan 2 adalah dari d ke c.
Contoh 2
Gambar 4 melukiskan sebuah logam PQ sepanjang l = 90 cm yang digerakkan dengan
kecepatan tetap v = 2 m/s sejajar dengan kawat lurus berarus i = 40 A. Batang tersebut berjarak x =
10 cm dari kawat. Hitunglah ggl induksi pada batang serta tentukanlah ujung batang yang
berpotensial tinggi.
Gambar 4
5
Jawab
Jika batang PQ digerakkan, elektron bebas pada batang akan bergerak yang akan
menimbulkan pengumpulan muatan pada kedua ujung batang. Akibatnya pada kedua ujung batang
terjadi perbedaan potensial. Karena tak ada simpal kawat, arus tak dapat mengalir terus. Karena itu
untuk menghitung ggl, kita bayangkan ada kawat berbentuk U seperti dilukiskan dengan garis putusputus pada Gambar 4.
Kita tidak dapat menggunakan persamaan ε = Blv karena fluks tidak homogen. Akan tetapi
untuk elemen dy maka perubahan B dalam dy dapat diabaikan dan persamaan di atas dapat
digunakan.
dε = B(y) v dy
(10)
dengan B(y) dari hukum Ampere adalah
B( y) =
μ0 i
2π y
(11)
Jadi dari persamaan (10) dan (11) diperoleh
ε=
=
1 μ 0 iv ⎛ 1 ⎞
μ0 i
μ iv 1 dy μ 0 iv
vdy = 0 ∫
=
ln y
=
ln⎜ ⎟
0,1 2π ⎝ 0,1 ⎠
2π y
2π 0,1 y
2π
batang
∫
μ 0 iv
(4π x 10 -7 )(40)(2)
ln 10 =
ln 10 = 3,68 x 10 -5 V = 36,8 μV
2π
2π
Arah ε dapat ditentukan dengan menggunakan hukum Lenz. Sebab timbulnya ggl induksi karena
batang PQ didorong ke kanan. Ggl induksi melawan ini dengan menimbulkan arus pada batang PQ
sehingga timbul gaya ke kiri, melawan dorongan kita. Dengan kaidah tangan kanan didapatkan bahwa
arus bergerak dari bawah ke atas. Jadi ujung yang berpotensial tinggi adalah ujung Q.Gauss
21.2 Generator Listrik
Generator mengubah energi mekanik menjadi energi listrik, yang merupakan kebalikan dari
cara kerja motor. Prinsip kerja dari generator adalah kumparan yang berputar dalam medan magnetic
seragam. Ujung kumparan diberi sebuah cincin yang dinamakan cincin selip yang berputar mengikuti
kumparan.
6
Fluks magnatik yang melalui kumparan adalah φm = NBA cos θ , dimana θ adalah sudut yang
dibentuk bidang kumparan dengan medan magnetik seragam B, N merupakan banyaknya lilitan dan
A luas kumparan.
Gambar Pengaruh Medan Magnet pada motor
Gambar Prinsip generator
GGL yang dihasilkan adalah :
ε = ε maks sin(ωt + δ )
ε maks = NBAω
ω adalah frekuensi sudut putar.
21.3 Transformator
Dengan pertimbangan efisiensi maka transmisi daya listrik dilakukan pada tegangan tinggi dan
arus kecil. Sebaliknya faktor keamanan dan alasan keselamatan menganjurkan pemakaian tegangan
yang rendah. Untuk menyatukan dua kepentingan yang berbeda ini maka diperlukan alat yang dapat
menaikkan atau menurunkan tegangan di dalam sebuah rangkaian dengan mempertahankan hasil
7
perkalian iV tetap konstan. Alat tersebut adalah transformator. Lambang untuk transformator dengan
inti besi adalah
Pada dasarnya transformator terdiri dari dua kumparan yang secara elektris tersekat satu sama
lain dan sama-sama terlilit pada satu inti dari besi seperti ditunjukkan oleh Gambar 14. Kumparan
yang menerima daya disebut kumparan primer dan yang mengeluarkan daya disebut kumparan
sekunder. Kumparan yang mana saja dapat dijadikan kumparan primer.
Gambar 14
Gaya gerak listrik imbas yang timbul dalam kumparan primer dan sekunder masing-masing
adalah
ε 1 = − N1
dΦ
dt
dan ε 2 = − N 2
dΦ
dt
(36)
Perbandingan ggl kumparan sekunder dengan primer adalah
ε2 N2
=
ε 1 N1
ε2 =
atau
N2
ε1
N1
(37)
Jika N2 > N1 maka transformator tersebut disebut penaik tegangan(step-up). Jika N2 < N1
disebut penurun tegangan (step-down).
Bila arus yang ditarik dari sumber adalah i1 dan arus yang ditarik dari kumparan sekunder i2,
maka dengan asumsi daya hilang diabaikan didapat
P1 = P2
atau
ε 1 i1 = ε 2 i2
(38)
Tetapi karena ε2/ε2 = N2/N1, maka
i2 =
N1
i1
N2
(39)
Yang dibicarakan di atas adalah transformator ideal, padahal pada prakteknya terjadi
kerugian daya. Daya yang hilang ini disebabkan oleh rugi panas i2R pada kedua kumparan (rugi
8
tembaga) dan rugi akibat histerisis dan arus pusar dalam inti transformator (rugi inti). Perbandingan
daya masukan dengan daya keluaran disebut efisiensi atau daya guna dari transformator, yaitu
Efisiensi =
daya keluaran daya masukan - daya hilang
=
daya masukan
daya masukan
(40)
Contoh 5
Pada sebuah transformator tertulis : tegangan primer 110 V, tegangan sekunder 6 V dan arus
maksimum yang dapat diambil dari transformator 300 mA. Hitunglah (a) perbandingan jumlah lilitan
kumparan sekunder dan primer, (b) arus maksimum yang dapat mengalir pada kumparan primer, dan
(c) daya maksimum yang dapat ditarik oleh beban.
Jawab
N2 ε 2
6
=
=
N1 ε 1 110
i1 =
ε2
6
i2 =
(300) = 18 mA
ε1
110
Bila arus sekunder yang ditarik lebih besar daripada 300 mA maka tegangan sekunder akan turun dari
6 V, karena adanya hambatan dalam atau hambatan keluaran dari transformator. Jika berhubungan
dengan arus yang besar, beban arus yang melebihi rating arus akan menyebabkan kawat lilitan
terbakar.
P2 = ε 2 i2 = (6)(0,3) = 1,8 watt m2
21.4 Indukstansi
Untuk memperlihatkan efek induksi/imbas dapat dilakukan dengan dua cara yaitu efek induksi
yang disebabkan oleh sebuah koil/kumparan yang dialiri arus dan dua buah koil berdekatan di mana
salah satu koil dialiri arus. Untuk membedakan nama kedua efek tersebut maka untuk satu koil
disebut induksi diri (self-induction) dan untuk dua koil disebut mutual induksi (mutual induction).
Induktansi Diri
Tinjau sebuah koil yang terbungkus rapat (close-packed) atau sebuah toroida atau bagian
tengah sebuah solenoida panjang dengan jumlah lilitan N. Di dalam ketiga jenis kumparan itu, fluks Φ
yang ditimbulkan dalam setiap lilitan oleh arus i adalah sama. Dari hukum Faraday, ggl induksinya
adalah
ε =−
d ( NΦ )
dt
(12)
9
dengan NΦ adalah banyaknya tautan fluks (flux linkages) yang merupakan kuantitas
karakteristik yang penting untuk induksi.
Jika tidak ada bahan-bahan magnetik seperti besi di dekatnya, maka kuantitas tersebut
sebanding dengan arus i.
NΦ = Li
(13)
dengan L adalah tetapan penbanding yang dinamakan induktansi (inductance).
Sehingga persamaan (12) menjadi
ε =−
d ( NΦ )
di
= −L
dt
dt
(14)
Atau ditulis
L=−
ε
(15)
di / dt
Satuan induktansi adalah Vs/A = henry (H)
Sebuah rangkaian atau bagian dari rangkaian yang mempunyai induktansi disebut induktor.
Lambang induktor adalah
Contoh 3
Sebuah toroida yang intinya udara mempunyai 100 lilitan. Jika luas penampangnya 10 cm2 dan
kelilingnya 0,5 m, hitunglah induktansi diri dari toroida tersebut.
Jawab
Fluks dalam toroida
Φ = BA =
μ 0 NiA
l
Karena seluruh fluks mencakup tiap lilitan maka induktansi diri
L=
NΦ μ 0 N 2 A (4π x 10 -7 )(100) 2 (10 -3 )
=
=
= 2,5 x 10 -5 H = 25 μH
l
l
0,5
Induktansi Bersama
Perhatikan Gambar 5 yang memperlihatkan dua buah kumparan yang lilitannya sangat rapat.
10
Gambar 5
Arus dalam kumparan 1 menimbulkan medan magnet yang sebagian lewat kumparan 2.
Misalkan fluks yang melewati kumparan 2 yang disebabkan oleh kumparan 1 adalah Φ21, maka
induktansi bersama dari kumparan 2 oleh kumparan 1 adalah
M 21 =
N 2 Φ 21
i1
atau
M21i1 = N2Φ21
(16)
Jika arus i1 berubah dengan waktu maka
M 21
Φ
di1
= N 2 21
dt
dt
(17)
Ruas kanan persamaan (17) adalah harga negatif dari ggl induksi ε2 yang timbul dalam
kumparan 2, sehingga
ε 2 = − M 21
di1
dt
(18)
Sekarang keadaanya kita balik, yaitu mengalirkan arus i2 pada kumparan 2. Dengan cara yang
sama seperti di atas, kita dapatkan
ε 1 = − M 12
di2
dt
(19)
Jadi dapat disimpulkan bahwa ggl induksi yang timbul di dalam kumparan yang manapun
adalah sebanding dengan kecepatan perubahan arus di dalam kumparan yang lainnya. Sehingga
walaupun konstanta M21 dan M12 kelihatan berbeda tapi, tanpa bukti, kita nyatakan konstanta tersebut
sama.
M21 = M12 = M
(20)
Maka persamaan (18) dan (19) dapat ditulis
11
ε 2 = −M
di1
dt
dan
ε 1 = −M
di2
dt
(21)
Contoh 4
Seperti diperlihatkan oleh Gambar 6, sebuah solenoida berarus i1 yang panjangnya 0,5 m terdiri dari
1000 lilitan kawat rapat. Sebuah kumparan kecil dengan 10 lilitan dililitkan di atas solenoida. Berapa
induktansi bersama untuk kedua lilitan tersebut.
Gambar 6
Jawab
Fluksi dalam solenoida
Φ 21 = BA =
μ 0 N1i1 A
l
Fluks Φ21 ini setara dengan Φ, yaitu fluks bersama total di dalam kumparan 1 dan 2, sehingga
M=
N 2 Φ 21 μ 0 AN 1 N 2 (4π x 10 -7 )(10 -3 )(10 3 )(10)
=
=
i1
l
0,5
= 2,5 x 10 -5 H = 25 μH
21.5 Energi dalam Medan Magnet
Tinjau dua buah kawat panjang sejajar yang mengangkut arus dalam arah yang sama. Karena
kedua kawat tersebut akan tarik menarik maka untuk memisahkan kedua kawat tersebut dibutuhkan
kerja. Kita dapat memperoleh kembali kerja yang tersimpan ini dengan membiarkan kedua kawat
tersebut pada kedudukan semula.
Untuk menurunkan pernyataan kuantitatif tentang penyimpanan energi dalam medan magnet,
kita tinjau Gambar 8. Persamaan (21) yang merupakan persamaan untuk rangkaian pada Gambar 8,
didapatkan dari teorema simpal. Sedangkan teorema simpal adalah bentuk lain dari hukum kekekalan
energi. Jika sekarang kita mengalikan kedua ruas pada persamaan (21) dengan i, didapatkan
12
ε i = i 2 R + Li
di
dt
(26)
Tafsiran fisis dari persamaan (26) adalah : Suku pertama menyatakan laju ggl mengantarkan
energi kepada rangkaian tersebut, Suku kedua menyatakan laju perubahan energi listrik menjadi
energi termal dalam hambatan., Suku ketiga, karena energi kekal, haruslah menyatakan penyimpanan
energi dalam medan magnet, yaitu
dU B
di
= Li
dt
dt
atau dU B = Li di
(27)
Dengan mengintegralkan didapat
UB
i
0
0
U B = ∫ dU B = ∫ Li di = 12 Li 2
(28)
yang menyatakan energi magnet total yang tersimpan dalam sebuah induktansi L yang
mengangkut arus i.
Selanjutnya kerapatan energi dapat dituliskan
U B 12 Li 2
=
uB =
Al
Al
(30)
dengan Al menyatakan volume medan magnet yang tercakup.
Dengan mengingat hubungan L = μ0N2A/l dan B = μ0Ni/l maka persamaan (30) dapat
dinyatakan
1 B2
uB =
2 μ0
(31)
Contoh 6
Sebuah koil mempunyai induktansi sebesar 5 H dan hambatan 20 Ω. Jika dipakaikan sebuah sumber
tegangan 100 V, berapakah energi yang tersimpan dalam medan magnet setelah arus mencapai nilai
maksimumnya.
Jawab
Arus maksimum diberikan oleh
i=
ε
R
=
100
=5 A
20
Energi yang tersimpan
13
U B = 12 Li 2 = 12 (5)(5) 2 = 62,5 J
Contoh 7
Bandingkanlah energi yang diperlukan untuk menghasilkan (a) medan listrik uniform sebesar 105 V/m
dan (b) medan magnet uniform sebesar 1 T (= 104 gauss), didalam sebuah volume kubus yang
sisinya 10 cm.
Jawab
a. U E = u E = 12 ε 0 E 2V0 = 12 (8,9 x 10 -12 )(10 5 ) 2 (0,1) 3 = 4,5 x 10 -5 J
b. U B = u BV0 =
(1) 2 (0,1) 3
B2
V0 =
= 400 J
2μ 0
(2)(4π x 10 -7 )
Jadi dapat disimpulkan bahwa jumlah energi yang dapat disimpan dalam sebuah medan magnet jauh
lebih besar daripada dalam medan magnet, dari contoh di atas, sekitar 107. Sebaliknya, energi yang
diperlukan untuk menghasilkan medan magnet jauh lebih besar dibanding medan listrik untuk volume
yang sama.
21.6 Rangkaian Listrik AC
Perhatikan bahwa untuk kondisi di mana R, C dan L dapat dilokalisir pada Gambar 1, maka
arus di dalam bagian simpal adalah sama.
Gambar 1
Sehingga kita dapat menganggap arus diberikan oleh
i = im sin (ωt - φ)
(2)
dengan im adalah amplitudo arus dan φ adalah sudut fasa antara ε dan i.
Untuk menyatakan im dan φ dalam εm, ω, R, C dan L, maka terlebih dahulu kita tinjau masingmasing elemen RLC dalam rangkaian terpisah.
Rangkaian Resistif
Gambar 2 memperlihatkan rangkaian resistor yang dihubungkan dengan sumber AC.
14
Gambar 2
Dari teorema simpal dan definisi hambatan didapatkan
VR = ε m sin ωt
(3)
VR = i R R
(4)
Dari (3) dan (4) didapat
⎛ε ⎞
i R = ⎜ m ⎟ sin ωt
⎝ R⎠
(5)
Persamaan (3) dan (5) memperlihatkan bahwa kuantitas VR dan iR adalah sefasa, yaitu
kuantitas-kuantitas tersebut mencapai nilai maksimumnya dalam waktu yang sama. Secara grafik
diperlihatkan dalam Gambar 3.
Gambar 3
Cara lain memeprlihatkan situasi di atas adalah dengan diagram fasor seperti diperlihatkan
dalam
Gambar 4
15
Fasor yang dinyatakan dengan panah hitam, berotasi berlawanan dengan arah perputaran
jarum jam dengan frekuensi sudut ω mengelilingi titik asal. Bahwa VR dan iR adalah sefasa
disimpulkan dari kenyataan bahwa fasor-fasornya terletak sepanjang garis yang sama.
Fasor-fasor tersebut mempunyai sifat : Panjang fasor sebanding dengan nilai maksimum dari
kuantitas yang terlibat, yaitu kuantitas εm untuk VR (persamaan (3)) dan kuantitas (εm/R) untuk iR
(persamaan (5)). Proyeksi fasor-fasor ke sumbu vertikal memberikan nilai sesaat (instantaneus value)
dari kuantitas-kuantitas yang terlibat.
Rangkaian Kapasitif
Gambar 5 memperlihatkan rangkaian sebuah elemen kapasitif yang dihubungkan dengan
sumber AC.
Gambar 5
Dari teorema simpal dan definisi kapasitansi, didapat
VC = ε m sin ωt
(6)
VC = q / C
(7)
Dari (6) dan (7) didapat
q = ε m C sin ωt
atau
iC =
dq
= ωCε m cos ωt
dt
(8)
Pembandingan persamaan (6) dan (8) memperlihatkan bahwa kuantitas-kuantitas VC dan iC
yang berubah-ubah terhadap waktu adalah berbeda fasa sebesar seperempat siklus. Situasi ini
dilukiskan secara grafik pada Gambar 6 dan secara fasor pada Gambar 7. Kita melihat bahwa VC
ketinggalan seperempat siklus dari iC. Sudut fasa φ dalam hal ini berharga -90°.
16
Gambar 6
Gambar 7
Karena alasan simetri dan notasi maka persamaan (8) kita tuliskan kembali dalam bentuk
iC =
εm
XC
cos ωt
(9)
dengan
XC =
1
ωC
(10)
disebut reaktansi kapasitif yang mempunyai satuan ohm.
Dapat disimpulkan bahwa jika suatu arus bolak balik yang amplitudonya im dan frekuensi
sudutnya ω, terdapat di dalam sebuah kapasitor maka beda potensial maksimum melalui kapasitor
tersebut (tak peduli bagaimanapun kompleksnya rangkaiannya) diberikan oleh
VC , m = i m X C
(11)
Rangkaian Induktif
Gambar 8 memperlihatkan rangkaian sebuah elemen induktif yang dihubungkan dengan
sumber AC.
17
Gambar 8
Dari teorema simpal dan definisi induktansi, didapat
VL = ε m sin ωt
(12)
VL = L (di / dt )
(13)
Dari (12) dan (13) didapat
di = (ε m / L) sin ωt dt
atau
i L = ∫ di = −(ε m / ωL ) cos ωt
(14)
Pembandingan persamaan (12) dan (14) memperlihatkan bahwa kuantitas-kuantitas VL dan iL
yang berubah-ubah terhadap waktu, mempunyai perbedaan fasa sebesar seperempat siklus. Situasi
ini dilukiskan secara grafik pada Gambar 9 dan secara fasor pada Gambar 10. Kita melihat bahwa VL
mendahului iL selama seperempat siklus. Sudut fasa φ antara VL dan iL dalam hal ini berharga +90°.
Gambar 9
Gambar 10
Sekali lagi karena alasan kekompakan notasi maka persamaan (14) kita tuliskan kembali dalam
bentuk
18
iL = −
εm
XL
cos ωt
(15)
dengan
X L = ωL
(16)
disebut reaktansi induktif yang juga mempunyai satuan ohm.
Dapat disimpulkan juga bahwa jika suatu arus bolak balik yang amplitudonya im dan frekuensi
sudutnya ω, terdapat di dalam sebuah induktor maka beda potensial maksimum melalui induktor
tersebut (tak peduli bagaimanapun kompleksnya rangkaiannya) diberikan oleh
V L ,m = im X L
(17)
RANGKAIAN SERI RCL
Sekarang kita perhatikan lagi Gambar 1 yang merupakan rangkaian seri dari R, C dan L. Dari
teorema simpal didapatkan
ε = VR + VC + VL
(18)
dengan harga maksimum
εm = imR + imXC + imXL
(19)
Walaupun persamaan (18) benar pada sebarang waktu, tapi tidak mudah untuk menentukan im
dan φ karena perbedaan-perbedaan fasa yang terdapat dalam suku-suku yang terpisah tersebut.
Karena itu kita gunakan diagram fasor seperti diperlihatkan pada Gambar 11.
Gambar 11
Dari Gambar 11 dapat diperoleh εm
19
ε m = VR2,m + (VL ,m − VC ,m ) 2
= (im R ) 2 + (im X L − im X C ) 2
(20)
= im Z
dengan Z = R 2 + ( X L − X C ) 2 disebut impedansi. Satuan impedansi adalah ohm.
Jadi kita dapat menyatakan im dengan menggunakan εm, ω, R, C, dan L, yaitu
im =
εm
R 2 + (ωL − 1 / ωC ) 2
(21)
Selanjutnya sudut fasa φ didapatkan dari
tg φ =
V L ,m − VC ,m
V R ,m
=
im ( X L − X C ) X L − X C
=
im R
R
(22)
yang tidak tergantung pada εm. Dengan menaikkan εm, maka im akan semakin besar, tetapi
tidak akan mengubah φ. Dengan kata lain, skala operasi berubah tetapi sifat operasinya tetap.
Contoh 1
Di dalam Gambar 1, misalkan R = 4 Ω, C = 150 μF, L= 60 mH, f = 60 Hz, dan εm = 300 V. Carilah (a)
XC, (b) XL, (c) Z, (d) im dan (e) φ.
Jawab
a. X C =
1
1
1
=
=
= 18 Ω
ωC 2πfC (2π )(60)(150 x 10 -6 )
b. XL = ωL = (2π)(60)(60 x 10-3) = 23 Ω
c. Z = R 2 + ( X L − X C ) 2 = (4) 2 + (23 − 18) 2 = 6,4 Ω
Perhatikan bahwa rangkaian tersebut lebih bersifat induktif karena XL > XC.
d. i m =
εm
Z
=
300
= 47 A
6,4
⎛ X − XC ⎞
⎛ 23 − 18 ⎞
e. φ = arctg⎜ L
⎟ = arctg⎜
⎟ = 51°
R
⎝ 4 ⎠
⎝
⎠
Karena XL > XC, maka φ positif dan εm mendahului im seperti yang disarankan Gambar 11, tetapi
seperti yang diharapkan, nilainya kurang dari 90°.
20
21.7 Osilator
Dalam sebuah rangkaian seri RCL, impedansi induktor dan kapasitor tergantung pada frekuensi
f sumber, maka arus pada rangkaian RLC juga tergantung pada frekuensi. Arus akan maksimum pada
suatu frekuensi jika :
2π fl −
1
=0
2π fC
Hasilnya akan didapatkan :
f0 =
1
2π
1
LC
Ini yang disebut dengan frekuensi resonansi rangkaian.
Jika R sangat kecil maka kita seperti mempunyai rangkaian LC, energi di dalam sebuah
rangkaian LC berosilasi, dengan frekuensi f0, antara induktor dan kapasitor, sebagian energi akan
terbuang di R.
Proses pengisian muatan yang berlangsung bolak-balik dari suatu pelat kapasitor ke pelat lain
melalui induktor, berulang terus menerus disebut dengan osilasi LC atau osilasi elektromagnetik.
Tidak hanya muatan yang berosilasi bolak-balik tetapi juga energi yangberosilasi.
21.8 Quis 21
B
1.
Kutub utara sebuah magnet digerakkan
menjauhi sebuah cincin logam, seperti dalam
gambar di samping. Tentukan arah arus di
dalam bagian cincin yang terdekat dengan
pembaca ! Berilah penjelasan singkat jawaban
anda dengan menggunakan Hukum Lenz !
U
50 cm
v
x
2.
Sebuah batang diletakkan di atas rangkaian.
Luas penampang rangkaian tertembus secara tegak lurus oleh medan magnet B = 0,15
T. Jika hambatan rangkaian R = 3 Ω, berapa besar gaya yang dibutuhkan untuk
menggerakkan batang dengan laju tetap v = 2 m/s ke kanan ?
3.
Induktansi sebuah kumparan yang terbungkus rapat yang terdiri 500 lilitan adalah 28
mH. Berapakah fluks magnet yang melalui kumparan tersebut bila arus 2,5 A ?
21