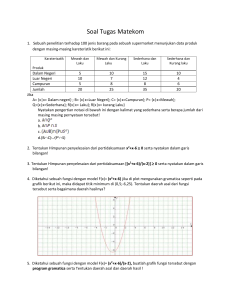
KALKULUS ( LIMIT )

KALKULUS
( LIMIT )
Diusulkan oleh :
Yayan Subagyo
( 07.02.5336 )
Yuventus Deklis BK ( 03.02.5144 )
Indra Gunawan
( 03.04.2149 )
JURUSAN TEKNIK INDUSTRI
FAKULTAS TEKNOLOGI INDUSTRI
INSTITUT SAINS & TEKNOLOGI “AKPRIND”
YOGYAKARTA
2009
KATA PENGANTAR
Terima kasih,mungkin hanya sepatah kata ini yang saya ucapkan kepada tuhan yang
maha esa karena berkat dan rahmat-Nya jualah sehingga saya dapat menyelesaikan penulisan
tugas makalah ini.
Pada sempatan ini, ijikan saya selaku penulis mengucapkan rasa terimakasih saya
kepada teman-teman saya yang telah membantu saya dalam menyelesaikan makalah ini, baik
dari proses penyusunan, pengetikan, sampai akhirnya makalah ini bisa selesai.
Akhirnya saya selaku penulis sangat mengharapkan masukan berupa saran, ataupun
kritikan
yang
bersifat
membangaun,
yang
pada
intinya
sangat
berguna
untuk
menyempurnakan penulisan makalah selanjutnya, dan semoga makalah ini dapat menjadi
sumber pengetahuan baru bagi pembacanya
KONSEP LIMIT
Dalam matematika, konsep Limit digunakan untuk menjelaskan sifat dari suatu fungsi,
saat argumen mendekati ke suatu titik, atau tak hingga; atau sifat dari suatu barisan saat
indeks mendekati tak hingga. Limit dipakai dalam kalkulus (dan cabang lainnya dari analisis
matematika) untuk mencari turunan dan kekontinyuan.
Konsep Limit mempunyai peranan yang sangat penting di dalam kalkulus dan
berbagai bidang matematika. Oleh karena itu, konsep ini sangat perlu untuk dipahami.
Meskipun pada awalnya konsep Limit sukar untuk dipahami, tetapi dengan kita memahami
secara sungguh-sungguh maka materi limit tidaklah begitu sulit.
Definisi Limit
Definisi Limit :
Atau X ≠
c
PENGERTIAN LIMIT
•
Limit fungsi f(x) untuk x mendekati a ditulis
.Nilai Limit fungsi
tersebut adalah harga yang didekati fungsi jika variabel fungsi tersebut
mendekati bilangan a. Proses mendekati ini bisa dari kiri (disebut limit kiri
ditulis
) dan bisa dari kanan (disebut limit kanan ditulis
).
•
Fungsi dikatakan mempunyai limit jika nilai limit kiri dan limit kanannya sama.
•
Untuk fungsi tunggal limit kiri dan kanan selalu sama sehingga tidak perlu kita
cari limit kiri dan kanannya, tetapi untuk fungsi majemuk harus diperiksa limit
kiri dan limit kananya.
LIMIT FUNGSI ALJABAR
1. Limit f ( x ) untuk x→a
Definisi : harga limit dari f (x) bila x mendekati a adalah L . ditulis limx→afx=L
Jika untuk € > 0 hingga berlaku | f (x) –L | < € bila 0 < 1 x – a | < & ( bilangan terkecil
) dan € ( bilangan positif)
Untuk menyelesaikan limx→afx=f (a)
v Jika
maka f(x) harus disederhanakan / diubah dengan cara :
Ø difaktorkan (untuk derajat 3 atau lebih pakai “porogapit”)
Ø jika ada akar dikali sekawan bentuk akarnya kemudian difaktorkan.
Contoh
a. limx→3x2+ 2x + 1(x + 2)
limx→39+ 6 + 15
=
limx→332+ 2.3 + 1(3 + 2)
165
= 315
1. limit f(x) untuk x mendekati
definisi : fungsi f (x) di katakana memiliki limit L bila x mendekati takterhingga di
tulis limx→∞f x=L
jika untuk € > 0 N > 0. Sehingga berlaku | f (x) – L < € bila x > N
untuk menyelesaikan nya yaitu :
Ø
Jika
Ø
Jika
terbesar.
f(x) diubah dahulu dengan cara dibagi x pangkat yang terbesar.
f(x) dikali sekawan dahulu baru dibagi dengan x pangkat yang
Contoh
a. lim→∞2x3-5x+85x3+9
= limx→∞2x3x3 - -5xx3 + 8 x35x3x3 + 9x3
=
limx→∞2-5x2+8x35+9x3
= limx→∞2- 5∞2 + 8∞35 + 9∞3
= limx→∞2-0+05+0
= limx→∞ 25
4. TEOREMA LIMIT
1. limit suatu fungsi konstanta nilainya sama dengan konstanta itu.
2. limit suatu fungsi identitas sama dengan nilai pendekatan peubahnya
3. limit jumlah beberapa fungsi sama dengan jumlah masing-masing limit fungsi. limit
selisih beberapa fungsi sama dengan selisih masing-masing limit fungsi.
4. limit hasil kali konstanta dengan suatu fungsi sama dengan hasil kali konstanta dengan
limit fungsi itu.
5. limit hasil kali beberapa fungsi sama dengan hasil kali masing-masing limit fungsi.
6. limit hasil bagi beberapa fungsi sama dengan hasil bagi masing-masing limitnya
dengan catatan limit penyebut tak boleh sama dengan nol.
7. limit fungsi pangkat n sama dengan pangkat n dari limit fungsi itu.
8. limit akar pangkat n dari suatu fungsi sama dengan akar pangkat n dari limit fungsi itu.
KONTINUITAS
Fungsi f (x) di sebut kontinu di x = x0 jika
i. f ( x0 ) terdefinisi
ii. limx→0fx ada
iii. limx→0fx=f (x0)
Fungsi f (x) disebut kontinu jika x = x0 . namaun jika salah satu atau lebih persyaratan
tidak terpenuhi maka di sebut diskontinu.
Contoh
a. Selidiki kekontinuan fungsi f(x)
X = 1 ( i ) f(X) 2X+3 =5
(ii) limx→1-2x+3=5
limx→1+fx8-3x=5
Limit kiri = limit kanan f(x) 2x+3 =5
F(x) 8-3x = 5
( iii ) limx→1= limx→1-f x= limx→1+f(x)
Karena ke tiga (3) syarat terpenuhi maka kontinu pada x = 1
X = 2 ( i ) f (x) x + 3 = 5
( ii ) limx→2- 8-3x=8-3.2=2
limx→2+ x+3=2+3=5
Limit kiri ≠ limit kanan
( iii ) f ( x) ≠ limx→2 f (x)
Diskontinu karena limit kiri ≠ limit kanan
PENYELESAIAN SOAL LIMIT
1. limx→4(2x-3)
=
limx→4(2.4-3)
= (8-3) = 5
2. limx→2x3-8x2-4
= x-2 x2+2x+4x-2 x+2
( x2+2x+4) (x+2)
( 22+2.2+4) (2+2)
( 4+4+4 ) ( 4 )
( 12 ) ( 4 ) =3
3. limx→∞2x+1x = limx→∞2xx + 1x 1
limx→∞2+ 1x1
limx→∞2+1x
limx→∞2+1∞
limx→∞2+0= 2
4. limx→3x2-5x+6x2-9 = x-3 (x-2)x-3(x+3)
(3-2)(3+3)
5. limx→3x2+ 3X-18x2-3x
=
16
= limx→3x+6(x-3)x(x-3)
3+6(3-3)3(3-3)
93 =3
6. limx→0x(x+30)x3+10x
= limx→0x(x+30)x(x2+10)
limx→00(0+30)0(02+10)
limx→0 3010 =3
7. limx→0x2+15Xx3+5X
=
limx→0X (X+15)X (x2+5)
limx→0(0+15)(02+5)
limx→0 155=3
8. limx→425-x2 = 25-16
9 =3
9. limx→3x3-27x2-9 = limx→3x-3( x2+3x+9)x-3( x+3)
limx→3x2+3x+9x+3
limx→332+3.3+93+3
limx→3276=92
10.limx→∞2x3x2+1
= limx→∞2x3x3x2x3 + 1x3
21x + 1x3
= 20+0= ∞
DAFTAR PUSTAKA
N. Soemartojo, Dra. (1983). Kalkulus ,ERLANGGA, Jakarta pusat.
www. Goggle.com
http://rasyid14.files.wordpress.com/2009/03/limit-fungsi-soal-jawab1.pdf.
http://matematikalc.890m.com/limit.htm