1.6 rules of inference

1.6 RULES OF INFERENCE
1
Argumen
• Argumen dalam logika adalah kumpulan sejumlah proposisi.
Seluruh proposisi dalam suatu argumen, kecuali proposisi
terakhir, disebut premis. Sedangkan proposisi terakhir disebut
kesimpulan.
• Suatu argumen dikatakan valid, apabila kebenaran seluruh
premis mengakibatkan kebenaran dari kesimpulan.
• Untuk mendeduksi proposisi baru dari proposisi yang telah ada
sebelumnya, digunakan aturan inferensi untuk membangun
argumen yang valid.
• Aturan inferensi merupakan alat untuk menentukan kebenaran
suatu argumen. Selain itu, dapat juga digunakan tabel kebenaran
untuk menunjukkan bahwa suatu argumen valid. Namun ini
tidak efisien dilakukan untuk argumen yang memuat banyak
2
proposisi.
Contoh Argumen
“Jika Anda memiliki password terkini, maka Anda dapat
mengakses jaringan.”
“Anda memiliki password terkini.”
Maka,
“Anda dapat mengakses jaringan.”
Argumen ini berbentuk:
p→q
p
∴q
3
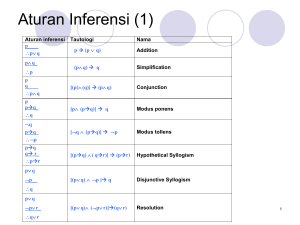
Aturan Inferensi
4
Aturan Inferensi (2)
5
Soal 1
Tunjukkan bahwa premis:
“Matahari tidak bersinar sore ini dan sore ini lebih dingin dari
kemarin,”
“Kita akan berenang hanya jika matahari bersinar,”
“Jika kita tidak berenang, maka kita akan naik perahu,” dan
“Jika kita naik perahu, maka kita akan sampai ke rumah sebelum
matahari terbenam”
akan memberikan kesimpulan:
“Kita akan sampai ke rumah sebelum matahari terbenam.”
6
Soal 2
Tunjukkan bahwa premis
“Jika Anda mengirim e-mail, maka saya akan menyelesaikan
penulisan program,”
“Jika Anda tidak mengirim email, maka saya akan tidur lebih
awal,”
“Jika saya tidur lebih awal, maka saya akan bangun dengan
segar”
akan memberikan kesimpulan:
“Jika saya tidak menyelesaikan penulisan program, maka saya
akan bangun dengan segar.”
7
Argumen yang Tidak Valid
((p → q) ∧ q) → p bukan merupakan tautologi
Contoh 1.
Jika Anda mengerjakan setiap soal dalam buku teks,
maka Anda akan belajar matematika diskrit.
Anda belajar matematika diskrit.
Jadi, Anda mengerjakan setiap soal dalam buku
teks.
8
Aturan Inferensi
untuk Pernyataan Berkuantor
x P(x)
P(c)
Universal instantiation
P(c) utk setiap c
 x P(x)
Universal generalization
x P(x)
P(c) utk suatu c
Existential instantiation
P(c) utk suatu c
 x P(x)
Existential generalization
9
Soal 3
Tunjukkan bahwa premis:
“Seorang mahasiswa di kelas ini tidak membaca
buku teks” dan
“Semua peserta kelas ini lulus ujian”
memberikan kesimpulan:
“Seseorang yang lulus ujian tidak membaca buku
teks.”
10
Universal Modus Ponens
∀x(P(x) → Q(x))
P(a), dengan a suatu anggota dari domain
∴ Q(a)
Soal 4.
Asumsikan bahwa pernyataan “Untuk setiap
bilangan bulat positif n, jika n>4, maka n2<2n”
adalah benar.
Gunakan universal modus ponens untuk
menunjukkan bahwa 1002<2100.
11
1.7 PENGANTAR BUKTI
12
Terminologi
• Teorema adalah pernyataan yang dapat
dibuktikan kebenarannya.
• Teorema yang dianggap kurang penting (kurang
berkontribusi) biasanya disebut proposisi.
• Kebenaran teorema ditunjukkan dengan
menggunakan bukti. Bukti adalah argumen valid
yang menyatakan kebenaran suatu teorema.
• Peryataan dalam suatu bukti dapat memuat
aksioma (atau postulat), yaitu pernyataan yang
diasumsikan benar.
13
Terminologi (2)
• Teorema yang kurang penting, namun membantu dalam
membuktikan hasil lain disebut lema. Bukti yang sulit biasanya
akan lebih mudah dipahami jika menggunakan sekumpulan
lema, yang setiap lemanya dibuktikan tersendiri.
• Akibat adalah teorema yang dapat dibuktikan secara langsung
dari teorema lain.
• Konjektur adalah pernyataan yang diajukan untuk menjadi
pernyataan yang benar, biasanya berdasarkan bukti parsial,
argumentasi heuristik atau intuisi seorang ahli. Apabila bukti
untuk suatu konjektur ditemukan, maka konjektur akan menjadi
teorema. Seringkali konjektur ditunjukkan salah, sehingga tidak
menjadi teorema.
14
Kuantifikasi Universal
dalam Teorema
Banyak teorema yang berlaku untuk seluruh anggota dari
suatu domain, seperti bilangan bulat atau bilangan real.
Walaupun pernyataan yang demikian memerlukan kuantifikasi
universal, dalam teorema seringkali dihilangkan.
Contoh 2.
Pernyataan
“Jika x > y, dengan x dan y bilangan real positif, maka x2 > y2.”
Sebenarnya bermakna
“Untuk setiap bilangan real positif x dan y, jika x > y, maka x2 >
y2.”
15
Bukti Langsung dan Bukti Tak Langsung
1. Bukti Langsung
Implikasi p  q dapat dibuktikan dengan menunjukkan
jika p benar maka q juga harus benar.
Soal 5. Berikan bukti langsung dari
“Jika n bilangan bulat ganjil maka n2 ganjil.”
2. Bukti Tak Langsung (Bukti dengan Kontraposisi)
Karena p  q ekivalen dengan q  p maka
p q dapat dibuktikan dengan menunjukkan bhw
q  p benar.
Soal 6. Berikan bukti tak langsung dari
“Jika n2 ganjil maka n ganjil.”
16
Bukti Kosong dan Bukti Trivial
Bukti kosong
Jika hipotesis p dari implikasi p  q salah, maka p  q selalu
benar, apapun nilai kebenaran dari q.
Soal 7. P(n): Jika n > 1, maka n2 > 1.
Tunjukkan P(0) benar.
Bukti trivial
Jika konklusi q dari implikasi p  q benar, maka p  q selalu
benar, apapun nilai kebenaran dari p.
Soal 8. P(n): Jika a, b integer positif dengan a  b,
maka an  bn.
Tunjukkan P(0) benar.
17
Bukti dengan Kontradiksi
Bukti Tak Langsung (Bukti dengan Kontradiksi)
Misalkan kita ingin membuktikan bahwa pernyataan p
benar. Di samping itu, kita bisa menemukan suatu
kontradiksi q sehingga ￢p → q benar. Karena q salah,
tetapi ￢p → q benar, kita dapat menyimpulkan bahwa
￢p salah, yang berarti p benar.
Soal 9.
1. Tunjukkan bahwa sedikitnya ada 4 hari yang sama dari
pilihan 22 hari sebarang.
2. Buktikan bahwa 2 irasional.
18
Bukti dengan
Kontraposisi vs Kontradiksi
Bukti dengan kontraposisi dapat dituliskan kembali sebagai bukti
dengan kontradiksi.
Dalam bukti dari p → q dengan kontraposisi, kita mengasumsikan
bahwa ￢q benar. Kita kemudian menunjukkan bahwa ￢p juga harus
benar.
Untuk menuliskan kembali bukti dengan kontraposisi dari p → q
sebagai bukti dengan kontradiksi, kita misalkan bahwa p dan ￢q
keduanya benar. Akibatnya, kita menggunakan langkah dalam bukti
dari ￢q →￢p untuk menunjukkan bahwa ￢p benar. Ini akan
memberikan kontradiksi p ∧￢p, yang merupakan akhir dari bukti.
Soal 10.
Berikan bukti dengan kontradiksi dari Soal 6
“Jika n2 ganjil maka n ganjil.”
19
Bukti dengan Ekivalensi
Untuk membuktikan teorema yang menggunakan
pernyataan bikondisional, yaitu pernyataan dalam bentuk p
↔ q, kita menunjukkan bahwa
p → q dan q → p keduanya benar.
Pendekatan ini berdasarkan tautologi
(p ↔ q) ↔ (p → q) ∧ (q → p).
Soal 11.
Buktikan teorema
“Jika n bilangan bulat, maka n ganjil jika dan hanya jika n2
ganjil.”
20
Contoh Penyangkal
Untuk menunjukkan bahwa suatu pernyataan dalam bentuk
∀x P(x) salah, kita hanya memerlukan satu contoh penyangkal, yaitu,
contoh x sehingga P(x) salah.
Contoh 3.
Tunjukkan bahwa pernyataan
“setiap bilangan bulat positif adalah hasil tambah dari tiga bilangan
kuadrat.”
adalah salah.
Solusi. Pernyataan ini benar untuk beberapa nilai, mis.
1=02+02+12; 2=02+12+12 ; 3=12+12+12 ; 4=02+02+22 ; 5=02+12+22 ;
6=12+12+22 .
Tapi kita tidak dapat mengekspresikan seperti di atas untuk bilangan 7.
Jadi bilangan 7 merupakan contoh penyangkal dari pernyataan di atas.
21
Kesalahan dalam Bukti
Soal 12.
Apa yang salah dalam “bukti” bahwa 1 = 2 ini?
“Bukti:” Misalkan a dan b bilangan bulat positif.
Langkah
Alasan
1. a = b
Diberikan
2. a2 = ab
Kalikan kedua ruas di (1) dengan a
3. a2 − b2 = ab − b2
Kurangkan kedua ruas di (2) dengan b2
4. (a − b)(a + b) = b(a − b) Faktorkan kedua ruas di (3)
5. a + b = b
Bagi kedua ruas di (4) dengan a − b
6. 2b = b
Ganti a dengan b di (5) dan sederhanakan
7. 2 = 1
Bagi kedua ruas di (6) dengan b
22
1.8 PROOF METHODS AND
STRATEGY
23
Pembuktian
”Finding proofs can be a challenging business”
Matematikawan bekerja dengan memformulasi konjektur dan
kemudian mencoba membuktikan bahwa konjektur tersebut benar
atau salah.
Ketika dihadapkan dengan pernyataan yang akan dibuktikan:
• terjemahkan setiap istilah dengan definisinya
• analisa arti dari hipotesis dan kesimpulan
• coba membuktikan dengan menggunakan salah satu dari metoda
pembuktian
Jika pernyataan berupa implikasi; coba buktikan dengan bukti
langsung. Bila gagal, coba dengan bukti tak langsung. Bila tidak berhasil
juga coba dengan bukti kontradiksi.
Bukti dengan Kasus
Kadangkala kita tidak dapat membuktikan teorema dengan menggunakan
argumen yang berlaku untuk semua kasus, sehingga digunakan bukti
dengan mempertimbangkan kasus yang berbeda secara terpisah.
Untuk membuktikan pernyataan dalam bentuk
(p1 ∨ p2 ∨ · · · ∨ pn) → q
tautologi
[(p1 ∨ p2 ∨ · · · ∨ pn) → q] ↔ [(p1 → q) ∧ (p2 → q) ∧ · · · ∧ (pn → q)]
dapat digunakan sebagai aturan inferensi.
Soal 13.
Buktikan bahwa jika n adalah bilangan bulat, maka n2 ≥ n.
25
Contoh 4
Buktikan bahwa jika n bulat dan tidak habis dibagi
oleh 2 atau 3 maka n2 – 1 habis dibagi 24.
Solusi.
n bilangan bulat dapat dinyatakan sebagai
n=6k+j, j {0,1,2,3,4,5}.
Karena n tidak habis dibagi oleh 2 atau 3 maka
n=6k+1 atau n=6k+5.
Jadi ada 2 kasus yg perlu diperhatikan.
Bukti Exhaustive
Beberapa teorema dapat dibuktikan dengan memperhatikan
sejumlah kecil contoh. Bukti demikian disebut bukti
exhaustive.
Bukti exhaustive merupakan salah satu bentuk bukti dengan
kasus di mana setiap kasus memeriksa satu contoh tertentu.
Secara umum, suatu pernyataan tidak dapat dibuktikan
dengan menggunakan contoh, kecuali jika domain
pembicaraan dapat direduksi menjadi contoh yang jumlahnya
berhingga dan bukti yang diberikan mempertimbangkan
semua contoh tersebut.
27
Contoh 5
Tunjukkan bahwa (n + 1)3 ≥ 3n jika n bilangan bulat positif dengan
n ≤ 4.
Solusi.
Digunakan bukti dengan exhaustion. Kita hanya perlu
membuktikan (n + 1)3 ≥ 3n untuk n = 1, 2, 3, dan 4.
Untuk n = 1, (n + 1)3 = 23 = 8 dan 3n = 31 = 3;
untuk n = 2, (n + 1)3 = 33 = 27 dan 3n = 32 = 9;
untuk n = 3, (n + 1)3 = 43 = 64 dan 3n = 33 = 27; dan
untuk n = 4, (n + 1)3 = 53 = 125 dan 3n = 34 = 81.
Dalam keempat kasus ini, terlihat bahwa (n + 1)3 ≥ 3n.
Kita telah menggunakan bukti dengan exhautive bahwa (n + 1)3 ≥
3n jika n bilangan bulat positif dengan n ≤ 4.
28
Contoh 6
Tunjukkan bhw tidak ada solusi bulat x dan y yang
memenuhi x2 + 3y2 = 8.
Solusi.
Karena x2 > 8 bila |x|  3 dan 3y2 > 8 bila |y|  2,
maka kasus tersisa yang harus diperiksa adalah untuk
x = -2, -1, 0, 1, atau 2 dan y = -1, 0 atau 1.
Untuk nilai x demikian didapat x2 = 0, 1 atau 4,
sedangkan 3y2 = 0 atau 3. Jadi nilai maksimum dari x2
+3y2 = 7.
Dengan demikian tidak ada x dan y bulat yang
memenuhi x2 +3y2 =8.
Bukti Eksistensi
1. Bukti Eksistensi Konstruktif
Contoh 7.
Tunjukkan bahwa ada bilangan bulat positif yang dapat
dituliskan sebagai dua penjumlahan berbeda dari dua bilangan
pangkat 3.
Solusi. 1729 = 103 + 93 = 123 + 13.
2. Bukti Eksistensi Nonkonstruktif
Contoh 8.
Tunjukkan bhw ada bilangan irrasional x dan y sehingga xy
rasional.
Solusi. Kita tahu bahwa 2 irrasional. Pandang 22. Jika ia
rasional maka terbukti. Jika tidak, perhatikan (22)2= 22=2.
Jadi terbukti ada pasangan (x=2, y =2) atau (x= 22 dan y=
2) yg salah satunya memenuhi xy rasional.
30
Bukti Ketunggalan
Dua bagian dalam bukti ketunggalan:
Eksistensi Menunjukkan bahwa ada elemen x yg memenuhi
sifat yg diinginkan.
Ketunggalan Menunjukkan bahwa jika y  x maka y tidak
memenuhi sifat yg diinginkan.
Contoh 9. Tunjukkan bahwa setiap bilangan bulat mempunyai
invers penjumlahan yang tunggal.
Solusi. Jika p bulat maka p+q = 0 ketika q = -p, dan q juga
bulat.
Untuk menunjukkan ketunggalan, misalkan ada r bulat
dengan r  q dan p+r=0. Maka p+q = p+r. Dengan
mengurangkan kedua ruas dgn p didapat q=r, kontradiksi dgn
r  q.
Jadi ada bilangan bulat q yang tunggal sehingga p+q=0.
31
Proses Maju & Mundur
Apa pun metoda yang digunakan, dalam melakukan proses
pembuktian diperlukan titik awal.
Proses maju:
hipotesis
aksioma & teorema
kesimpulan
Namun seringkali, proses maju sukar untuk digunakan dalam
pembuktian sesuatu yang tidak sederhana. Sehingga kita
harus mengkombinasikan dengan proses mundur.
Contoh 10
Tunjukkan bahwa untuk setiap bilangan real positif x dan
y yang berbeda berlaku
(x+y)/2 > xy.
Solusi.
• B: (x+y)/2 > xy
• B1: (x+y)2 /4 > xy
• B2: (x+y)2 > 4xy
• B3: x2 +2xy+y2 > 4xy
• B4: x2 - 2xy+y2 > 0
• B5: (x-y)2 > 0
• B6: x  y.
Bukti.
Karena x dan y berbeda maka (xy)2 > 0.
Ini berarti x2 +2xy+y2 > 4xy.
Sehingga, (x+y)2 > 4xy yang
memberikan (x+y)/2 > xy.
Contoh 11
Tunjukkan bahwa jika segitiga siku-siku RST dengan sisi tegak r, s,
dan sisi miring t mempunyai luas t2/4, maka segitiga tersebut
sama kaki.
Solusi.
F: Segitiga RST dengan sisi r, s dan sisi miring t dengan luas t2/4.
F1: rs/2 = t2/4
F2: r2+s2 = t2
F3: rs/2 = (r2+s2)/4
t
2
2
F4: (r -2rs+s ) = 0
r
2
F5: (r-s) = 0.
B2: r-s = 0
B1: r = s
s
B: Segitiga RST sama kaki.
Contoh 11 (2)
Bukti 1.
Dari hipotesis dan rumus luas segitiga siku-siku,
Luas RST = rs/2 = t2/4.
Hukum Pythagoras memberikan r2+s2=t2, dan bila
r2+s2 disubstitusikan kedalam t2, dengan sedikit
manipulasi aljabar didapat (r-s)2=0.
Sehingga r=s dan segitiga RST samakaki.
Bukti 2.
Hipotesis dengan hukum Pythagoras
menghasilkan r2+s2=2rs; sehingga (r-s) = 0.
Maka segitiga RST samakaki.
Contoh 12. The Stone Game
Dua orang memainkan suatu permainan dengan
bergantian mengambil 1, 2, atau 3 batu pada setiap
pengambilan dari suatu kotak yg pada awalnya
berisi 15 batu.
Orang yang mengambil batu terakhir adalah
pemenangnya.
Tunjukkan bahwa pemain pertama dapat selalu
menang, tidak peduli apa yang dilakukan oleh
pemain kedua.
The Stone Game - Proses Mundur
Pemain 1
Pemain 2
0
1, 2, 3
4
5, 6, 7
8
9, 10, 11
12
13, 14, 15
The Stone Game - Bukti
Teorema 1.
Pemain pertama selalu dapat “memaksakan” kemenangan.
Bukti.
Pemain 1 dapat mengambil 3 batu, meninggalkan 12.
Setelah giliran pemain 2, terdapat 11, 10, atau 9 batu yang
tinggal. Dalam setiap kasus tersebut, pemain 1 dapat
mengurangi jumlah batu yang tertinggal menjadi 8.
Maka, pemain 2 dapat mengurangi kembali menjadi 7, 6, atau
5. Akibatnya, pemain 1 dapat meninggalkan sejumlah 4 batu.
Sehingga pemain 2 harus meninggalkan 3, 2, atau 1.
Pemain 1 kemudian mengambil semua batu yang tersisa dan
memenangkan permainan.
Konjektur
Buku matematika secara formal hanya menyajikan
teorema dan bukti saja. Melalui penyajian seperti ini,
kita tidak dapat mengetahui proses pencarian
(discovery process) dalam matematika
Proses ini meliputi:
• mengeksplorasi konsep & contoh,
• merumuskan pertanyaan,
• memformulasi konjektur, dan
usaha menjawab konjektur dengan bukti atau contoh
penyangkal.
Formulasi Konjektur
Konjektur diformulasikan dengan didasarkan
pada beberapa possible evidence:
• pengamatan beberapa kasus khusus
• identifikasi pola
• mengubah hipotesis dan kesimpulan dari
teorema yang telah dikenal sebelumnya
• intuisi dan kepercayaan
40
Contoh 13
Perhatikan fakta berikut ini.
24 – 1 = 15 = 3  5
25 – 1 = 31 prima
26 – 1 = 63 = 7  9
28 – 1 = 255 = 5  51
34 – 1 = 80 = 8  10
Kita tahu bhw xn – 1 = (x-1)(xn-1 +xn-2 + … + x + 1)
Namun, faktorisasi ini bermasalah bila x=2.
Konjektur 1.
Bilangan an-1 komposit jika a > 2 atau jika a=2 dan n
komposit.
Contoh 13 - Bukti
Kasus i)
Bila a > 2 maka (a-1) adalah faktor dari an-1
karena an – 1 = (a-1)(an-1 +an-2 + … + a + 1)
dan 1 < (a-1) < (an-1).
Kasus ii)
Bila a=2 dan n komposit maka
ada s dan t sehingga n = st dengan 1 < s  t < n.
Sehingga, 2s-1 faktor dari 2n-1
karena 2n – 1 = (2s-1)(2s(t-1) +2s(t-2) + … + 2s + 1).
Jadi 2n – 1 komposit.
Dengan demikian Konjektur 1 menjadi teorema.
Konjektur dan Contoh Penyangkal
Apakah ada fungsi f sehingga f(n) prima
untuk semua bilangan bulat positif n ?
Konjektur 2. f(n) = n2 – n +41.
Karena f(1) = 41, f(2) = 43, f(3) = 47, f(4)= 53,
….
Oopps! Tapi… f(41) = 412 komposit. Jadi f(n)
bukan fungsi penghasil bilangan prima.
Konjektur salah.
Bahkan Matematikawan Besar dapat
Mengajukan Konjektur yang Salah!
• Euler memformulasikan conjecture bahwa untuk
n>2, jumlah dari n−1 buah pangkat ke-n bilangan
bulat positif bukanlah merupakan bilangan pangkat
ke-n.
Benar untuk semua kasus yang diperiksa selama 200
tahun, namun tidak ada bukti yang ditemukan.
• Akhirnya, pada tahun 1966, Lander dan Parkin
menemukan counter-example untuk n=5
275 + 845 + 1105 + 1335 = 1445.
Counter-example juga ditemukan untuk n=4, tetapi
belum ada untuk n>5.
Beberapa Konjektur Terkenal (1)
Fermat’s Last Theorem
(1637)
Persamaan
xn + yn = zn
tidak mempunyai solusi
bulat x, y, dan z dengan xyz
 0 dan n > 2.
Dibuktikan tahun 1995 oleh
Andrew Wiles.
Beberapa Konjektur Terkenal (2)
Goldbach’s Conjecture (1742)
Dalam suratnya kepada Euler, Goldbach
menulis
“Setiap bilangan ganjil n, dengan n > 5,
dapat ditulis sebagai jumlah 3
bilangan prima.”
Menurut Euler, ini ekivalen dengan
“Setiap bilangan genap n, dengan n > 2,
dapat ditulis sebagai jumlah 2
bilangan prima.”
Telah dicek dengan komputer bahwa
Goldbach’s conjecture benar
utk semua bilangan  4 . 1018.
Beberapa Konjektur Terkenal (3)
The Twin Prime Conjecture
Twin prime adalah pasangan bilangan prima dengan selisih 2, seperti 3 dan
5, 5 dan 7, 11 dan 13, 17 dan 19, dan 4967 dan 4969.
Twin prime conjecture menyatakan bahwa ada tak hingga banyaknya twin
primes.
Hasil yang telah dibuktikan adalah jika h suatu bilangan
genap, maka terdapat tak hingga banyaknya bilangan
prima p sehingga p + h merupakan bilangan prima atau
hasil kali dari 2 bilangan prima (oleh J. R. Chen pada 1966).
Rekor dunia untuk twin primes (ditemukan pada Desember 2011 oleh
PrimeGrid, suatu distributed computing project di Berkeley Open
Infrastructure for Network Computing), adalah
3756801695685 · 2666669 ± 1
yang memiliki 200700 digit desimal.
Beberapa Konjektur Terkenal (3-cont)
Pada 13 Mei 2013, Yitang Zhang (University of New Hampshire)
membuktikan bahwa ada tak hingga banyaknya pasangan bilangan
prima dengan selisih 70 juta.
WHY 70 MILLION?
Pada 4 Juni 2013, Terence Tao (University of California, Los Angeles)
menginisiasi “Polymath Project,” suatu kolaborasi terbuka untuk
memperbaiki batas tersebut.
Pada 27 Juli 2013, 70 juta diturunkan menjadi 4,680.
Pada 19 November 2013, James Maynard (Oxford University dan
University of Montreal) mengajukan suatu metoda baru yang
menurunkan kembali batas menjadi 600.
Pada 14 April 2014, dengan menggunakan metoda Maynard,
Polymath Project telah berhasil menurunkan batas menjadi 246.
James Maynard memperoleh Ramanujan Prize 2014, Whitehead
Prize 2015, dan European Mathematical Society Prize 2016 atas
kontribusinya dalam teori bilangan.
48
Beberapa Konjektur Terkenal (4)
The 3x+1 Conjecture
Collatz problem, Hasse’s algorithm, Ulam’s
problem, Syracuse problem, Kakutani’s problem
(1950an)
Misalkan T suatu transformasi yang memetakan
bilangan genap x ke x/2 dan bilangan ganjil x ke
3x + 1.
Semua bilangan bulat x, apabila diterapkan
transformasi T secara berulang, pada akhirnya
akan mencapai 1.