PERANCANGAN PERANGKAT LUNAK PENERAPAN INTEGRAL

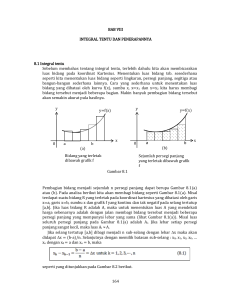
Sudi Suryadi
J. Informatika AMIK-LB Vol.2 No.1/Januari/2014
PERANCANGAN PERANGKAT LUNAK PENERAPAN INTEGRAL DALAM
MENGHITUNG ISI PERPUTARAN KURVA
Oleh :
SUDI SURYADI, S.Kom, M.Kom
Dosen Prodi Manajemen Informatika, AMIK Labuhanbatu
Rantauprapat, Medan; [email protected]
ABSTRAK
Integral adalah salah satu ilmu perhitungan kalkulas yang merupakan kebalikan dari
fungsi turunan. Secara umum, fungi integral dapat dibedakan menjadi fungsi integral tak tentu
dan fungsi integral tentu. Fungsi Integral tak tentu tidak memiliki batas nilai variable sedangkan
funsi integral tentu ini sering digunakan untuk menyelesaikan persoalan dalam bidang ilmu
pengetahuan.
Dengan adanya aplikasi Perancangan Perangkat Lunak Penerapan Fungsi Integral
Tentu untuk Menghitung Isi Benda Putar yang dibentuk dari Perputaran Kurva, program ini
dapat digunakan untuk mempermudah penggambaran grafik secara manual dan dapat
digunakan sebagai media alternatif untuk membantu mengerjakan penerapan fungsi integral
tetu untuk menghitung isi benda putar.
Keyword : kurva, hitung, integral, perputaran,
Benda Putar yang dibentuk dari Perputaran
Kurva”.
1.2 Perumusan Masalah
Berdasarkan latar belakang pemilihan
judul, maka yang menjadi permasalahan
adalah bagaimana penggambaran grafik fungsi
dan proses penyelesaian funsi integral untuk
menghitung isi / volume dari fungsi kurva
yang membentuk benda putar tersebut.
1.3 Tujuan dan Manfaat Penulisan
Tujuan penelitian ini adalah untuk
merancang suatu perangkat lunak yang mampu
menggambarkan
fungsi
kurva
dengan
menggunakan fungsi integral tentu secara
cepat dan tepat.
Manfaat penyusunan penilitian ini yaitu :
1. Menjadi perangkat lunak alternative
untuk menggambarkan fungsi kurva
secara cepat.
2. Membantu
pembelajaran
fungsi
integral
3. Menambah pengetahuan pembaca cara
membuat perangkat lunak dengan
penerapan fungsi integral tertentu
I. PENDAHULUAN
1.1 Latar Belakang
Apabila suatu kurva dilakukan perputaran
terhadap sumbu x atau sumbu y sejauh 360˚
(satu kali putaran), maka terjadilah suatu
benda pejal yang disebut benda putar . isi
(volume) dari bangun ruang tersebut dapat
dihitung dengan menggunakan integral tentu.
Integral adalah salah satu ilmu perhitungan
kalkulas yang merupakan kebalikan dari
fungsi turunan. Secara umum, fungi integral
dapat dibedakan menjadi fungsi integral tak
tentu dan fungsi integral tentu. Fungsi Integral
tak tentu tidak memiliki batas nilai variable
sedangkan funsi integral tentu ini sering
digunakan untuk menyelesaikan persoalan
dalam bidang ilmu pengetahuan .
Berdasarkan uraian diatas, penulis
bermaksud untuk meranang suatu perangkat
lunak yang mampu menggambarkan fungsi
kurva dan juga mampu untuk menghitung isi
atau volume dari yang membentuk benda putar
dengan mengajukan penelitian yang berjudul
“Perancangan Perangkat Lunak Penerapan
Fungsi Integral Tentu untuk Menghitung Isi
22
Sudi Suryadi
J. Informatika AMIK-LB Vol.2 No.1/Januari/2014
besar, contoh : A,B,C, … dan elemen-elemen
atau anggota dari himpunan dilambangkan
dilambangkan dengan menggunakan huruf
kecil, Contoh : a,b,c, …
Himpunan
dapat
dituliskan
dengan
menggunakan dua metode yaitu :
1. Metode Roster yaitu dengan cara
mencantumkan seluruh anggota dari
himpunan tersebut. Contohnya himpunan
A = {Andi,Budi,Chandra}
2. Metode Rule yaitu dengan cara
menyebutkan satu atau beberapa sifat dari
himpunan tersebut. Contohnya himpunan
A = {x | x adalah bilangan prima}
Notasi Himpunan yang digunakan adalah ∈,
contoh : 2 ∈ A yang berarti 2 adalah elemen
dari A atau 2 anggota dari A.
2.1.2 Jenis-jenis Himpunan
Secara garis besar, himpunan terdiri
dari 3 jenis, yaitu :
1. Himpunan terhingga adalah suatu
himpunan dimana elemen-elemen nya
terhingga.
Contohnya
himpunan
mahasiswa AMIK – Labuhanbatu
angkatan 2002
2. Himpunan tak terhingga adalah himpunan
yang
elemennya
tidak
terhingga.
Contohnya himpunan bilangan genap.
3. Himpunan kosong adalah himpunan yang
tidak mempnyai elemen sama sekali dan
dinyatakan dengan notasi ∅ atau { } .
Contohnya himpunan bilangan prima yang
lebih kecil dari nol.
2.1.3 Relasi Antar Himpunan
Relasi-relasi yang terdapat pada
himpunan adalah :
1. Ekivalen
Himpuanan A dikatakan Ekivalen
dengan himpunan B jika dan hanya jika
cardinal (jumlah elemen) dari kedua
himpunan tersebut sama. Dinotasikan
dengan A~B↔|A| = |B|
Contoh : jika A = {1,3,5,9} dan
B={a,b,c,d} maka A~B.
untuk menghitung isi benda putar yang
dibentuk dari perputaran kurva.
1.4 Pembatasan Masalah
Karena keterbatasan waktu dan
pengetahuan penulis, maka ruang lingkup
permasalahan dalam merancang perangkat
lunak ini antara lain :
1. Input dari perangkat lunak berupa :
a. Jenis perputaran (terhadap
sumbu x atau sumbu y).
b. Fungsi kurva berupa fungsi
persamaan kuadrat dengan satu
variable dan jumlah fungsi
maksimal dua buah.
c. Batas-batas dari kurva yang
akan dilakukan perputaran .
2. Perangkat
lunak
akan
menggambarkan grafik fungsi
3. Perangkat lunak akan menampilkan
langkah perhitungan.
4. Perangkat lunak dirancang dengan
menggunakan bahasa pemrograman
Visual Basic 6.0. .
1.5 Metodologi Penyelesaian Masalah
Langkah-langkah pembuatan perangkat
lunak ini antara lain :
1. Membaca dan mempelajari Bukubuku kalkulus yang bberhubungan
dengan integral.
2. Mempelajari penerapan integral
dengan menghitung volume benda
putar.
3. Merancang
antarmuka
pemakaian(interface)
4. Merancang Perangkat lunak yang
mampu menggambarkan fungsi
kurva dan menghitung isi benda
putar yang dibentuk dari perputaran
kurva dengan menggunakan fungsi
integral tertentu.
5. Melakukan Proses pengujian dan
perbaikan terhadap kesalahan yang
timbul
II. LANDASAN TEORI
2.1 Himpunan
2.1.1 Definisi
Himpunan adalah kumpulan dari
beberapa unsur yang memiliki sifat atau
keterkaitan tertentu. Suatu himpunan biasanya
dilambangkan dengan menggunakan huruf
2. Himpunan Bagian
Himpunan A dikatakan bagian dari
himpunan B,jika dan hanya jika setiap
elemen A merupakan elemen dari B ,
yang memungkinkan bahwa A=B .
23
Sudi Suryadi
J. Informatika AMIK-LB Vol.2 No.1/Januari/2014
Dalam hal ini dikatakan A adalah subset
dari B .
Dinotasikan dengan : A ⊆ B
Contoh : A = {1,3}; B = {1,3,5,7,9}
maka A ⊈ B karena 3 ∈ A tetapi 3∉ B
sedangkan dikatakan A ⊆ C karena
elemen A juga elemen C
Untuk menyatakan bahwa A asdalah
himpunan bagian dari B tetapi A ≠ B;
ada setidaknya satu elemen di B yang
tidak ada di A . Dalam hal ini A adalah
proper subset dari B . Dinotasikan
dengan A ⊂ B karena A adalah sebuah
subset dari B , Tetapi A ≠ B sedangkan
dikatakan A ⊈ C karena A=C,meskipun
A adalah subset dari C.
2.
3.
4.
2.1.4
Diagram Venn
Salah satu cara untuk menggambarkan
relasi antara dua himpunan atau lebih adalah
dengan menggunakan diagram venn, dimana
suatu himpuanna dinyatakan sebagai luas dari
suatu bidang yang dibatasi oleh lengkungan
tertutup da digambarkan dengan himpunan
semestanya.
5.
Dinotasikan dengan : A ∪ B = {x | x ∈
A atau x ∈ B}
Irisan (Intersection)
Himpunan irisan dari himpunan A dan
B adalah suatu himpunan yang
anggota-anggotanya dimiliki oleh A
dan juga dimiliki oleh B secara
bersamaan. Dinotasikan dengan : A ∩
𝐵 = {x | x ∈ A atau x ∈ B}
Komplemen suatu himpunan (Absolute
complement)
Komplemen dari suatu himpunan dari
elemen-elemen
yang
merupakan
anggota semesta tapi bukan anggota A.
Dinotasikan dengan : A = {x | x ∈ U
atau x ∉ B}.
Selisih dari 2 buah himpunan (The
relative complement)
Himpunan selisih dari 2 himpunan A
dan B adalah himpunan dari elemenelemen yang merupakan anggota dari
A tetapi bukan anggota dari B .
Dinotasikan dengan A – B = { x | x ∈
A dan x ∉B } = A ∩ 𝐵
Beda
Setangkup
(Symmetric
difference).
Beda setangkup dari himpunan A dan
B adalah suatu himpunan yang
elemennya ada pada himpunan A atau
B , tetapi tidaka ada pada keduanya.
Dinotasika dengan : A ⊕ B = (A ∪ B)
– (A ∩ 𝐵 )
2.2
Relasi dan Fungsi
2.2.1 Relasi
Relasi yaitu hubungan antara objek-objek.
Ada dua definisi tentang Relasi yaitu:
1. Hasil kali Kartesian
Perkalian kartesian (Crtesian Products)
dari himpunan A dan B adalah himpunan
yang elemnnya semua pasangan terurut
(ordered pairs) yang mungkin terbentuk
dengan
komponen
pertama
dari
himpunan A dan komponen kedua dari
Himpunan B . Dinotasikan dengan :
Gambar 2.1 Diagram Venn
2.1.5 Operasi Hantar Himpunan
Operasi-operasi yang berlaku pada
himpunan,antara lain:
1. Gabaungan (Uniom).
Himpunan
gabungan
dari
dua
himpunan A dan B adalah dimana
himpunan anggota-anggotanya adalah
anggota yang berada di A atau berada
di B atau berada dikedua-duanya.
A × B = {(x,y) | x ∈ A atau y ∈ B}
Contoh : A = {a,b) dan B ={1,2,3} maka
A
×
B
=
{(a,1),(a,2),(a,3),(b,1),(b,2),(b,3)}.
24
Sudi Suryadi
J. Informatika AMIK-LB Vol.2 No.1/Januari/2014
2.2.3
Jenis-jenis fungsi
Misalkan A dan B merupakan dua
himpunansembarang dan f adalah fungsi dari
A ke B, atau dituliskan : f : A→B , maka
fungsi dapat dibagi menjadi :
1. Fungsi injektif atau satu-satu : jika
elemen-elemen yang berbeda dalam
domain A mempunya range yang berbeda.
2. Relasi pada himpunan
Relasi biner R antara x dan y adalah
himpunan bagian dari x × y. jika (x,y) ∈
R, ditulis x R y dihubungkan dengan y
oleh R, dan jika (x,y) ∉ R maka ditulis x
R y artinya x dihubungkan y oleh R,dan
jika (x,y) ∉ R,maka ditulis x R y artinya
x tidak dihubungkan dengan y oleh
relaris R . Dinotasikan dengan : R ⊆
(A×B).
Contoh P = {2,4,8,9,15} dan Q =
{2,3,4}. Jika didefinisikan relasi R dari P
ke Q dengan (p,q) ∈ R , jika p habis
dibagi q maka diperoleh R =
{(2,2),(4,2),(4,4),(8,2),(8,4),(9,3),(15,3)}
1
A
2
B
3
c
Gambar 2.3 Fungsi Injektif
2. Fungsi subjektif jika setiap elemen
himpunan B merupakan bayangan dari
satu atau lebih elemen himpuna A . jadi
fungsi f adalah onto bila semua elemen B
merupakan daeraah hasil dari f.
A
B
2.2.2 Fungsi
Definisi suatu relasi dari himpunan B
dikatakan fungsi pemetaan jika :
1. Setiap Anggota A memiliki
pasangan tepat 1 di B .
2. Setiap
anggota
A
habis
dipasangkan dengan anggota B .
Dapat ditulis f : A → B yang
artinya f memetakan A ke B.
Beberapa Istilah yang haris dipahami dalam
mempelajari konsep fungsi adalah :
a. Himpunan A disebut sebagai domain f
atau disebut juga dengan daerah
definisi dari f.
b. X ∈ A,dikatakan sebagai prpeta dari y
∈ B,dikatan peta dari x ∈ 𝐴
c. Himpunan dari y= f(x) di B dinamakan
sebagai range f.
Contoh :
A
1
B
2
C
3
D
Gambar 2.4 fungsi surjektif
3. Fungsi bijektif : jika dan hanya jika fungsi
tersebut injektif dan juga surjektif.
A
B
A
1
B
2
A
1
c
3
B
2
C
Gambar2.2 Contoh dari fungsi
Keterangan Gambar 2.2 :
= {1,2,3}
3
D
Domain f
Kodomai
n f= {a,b,c}
Range f
= {a,c}
Gambar 2.5 Fungsi bijektif
4. Fungsi invers (balikan )
25
Sudi Suryadi
J. Informatika AMIK-LB Vol.2 No.1/Januari/2014
5. Balikan fungsi dilambangkan dengan f ˉⁱ .
misalkan a aadalah anggota himpunan A
dan b adalah anggota himpunan B . maka
f ˉⁱ (b)=a jika f(a)=b . Contoh :A ={1,2,3}
dan B = {x,y,z} adalah fungsi injektif
(satu-satu), dimana f = {(1,x), (2,y),
(3,z)}] maka balikan fungsi f adalah f ˉⁱ =
{(x,1),(y,2),(z,3)}
koordinat ditunjukkan dengan simsymbol,b).
contoh : titik P mempunyai koordinat (a,b) dan
titik yang mempunyai koordinat (-a,-b).
y
B
P
-a
O
x
Q
2.3 Fungsi dan Grafik
2.3.1 Variabel fungsi
Sebuah variable sebuah symbol yang
mengasumsikan sembarangan nilai dari suatu
himpunan nilai-nilai dan biasanya digunakan
huruf-huruf pada akhir abjad seperti x, y, z, u,
v, w. sebuah konstanta adalah sebuah symbol
yang berlaku hanya untuk satu nilai khusus
dan biasanya menggunakan huruf-huruf pada
awal abjad seperti a, b, c.
Sebuah variable y dikatakan sebuah
fungsi dari sebuah variable x apabila ada
hubungan antara x dan y sedemikian rupa
sehingga untuk tiap-tiap harga x dapat
diasumsikan ada satu hubungan atau lebih
dengan harga y. Contoh : y = x2 – 5x +2
mendefinisikan hubungan antara variabel x
dan y jadi apabila x=0, 1, 2, -1 maka masingmasing y= -2, -2, -4, 8.
Variabel z dikatakan sebagai fungsi dari
dua variabel yaitu variabel x dan y apabila ada
sebuah hubungan sedemikian rupa sehingga
tiap-tiap pasangan harga x dan y bersesuaian
dengan satu atau lebih harga z maka x=a dan
y=b asalkan fungsi terdefinisikan untuk hargaharga itu . Contoh : f(x,y)= x3+ xy2– 2x, maka
f(2.3) =23 + 2.32 – 2.3 = 20.
2.3.2 Koordinat tegak lurus
Sistem koordinat tegak lurus digunakan
untuk membentuk sebuah gaambar dari
hubungan antara dua variabel. Dua garis yang
slaing tegak lurus dinamakna sumbu
koordinat, perpotongannya diberi label O dan
disebut titik asala. Garis yang mendatar sumbu
x (horizontal) dan garis tegak dinamakan
sumbu y (vertikal). Misalkan diberikan sebuah
titik P pada bidang xy, titik P tegak lurus ke
sumbu x dan sumbu y .Nilai-nilai dari x dan y
pada titik-titik dimana sumbu x dan y bertemu
secara tegak lurus masing-masing menentukan
absis dan ordinat dari titik P . Koordinat-
-b
Gambar 2.6 Koordinat P(a, b) dan Q(-a, -b)
2.3.3 Grafik fungsi
Grafik sebuah fungsi adaah tempat kedudukan
dari semua titik (x,y) yang memenuhi
persamaan y= f(x).secara umum, grafik dari y
= ax + b dimana a, b sebagai konstanta adalah
sebuah garis lurus yang disebut funsi linear.
Disebut sebagai fungsi linear karena dua titik
membentuk sebuah garis lurus, maka hanya
dua titik yang perlu digambarkan dan ditarik
garis penghubungnya.
Gambar 2.7 Grafik Fungsi Liniar
Grafik dari y = ax2 + bx + x mewakili parabola
yang titik puncaknya merupakan titik
maksimum atau minimum, tergantung masingmasing apakah a negative atau positif. Fungsi
f(x) = ax2 + bx + x disebut juga fungsi kuadrat
26
Sudi Suryadi
J. Informatika AMIK-LB Vol.2 No.1/Januari/2014
5. lim
. Gambar dibawah menunjukkan grafik fungsi
kuadrat dengan titik terendah P , disebut titik
minimum atau titik parabola.
𝑥→𝑐
lim
𝑥→𝑐
6. lim
𝑥→𝑐
lim
𝑥→𝑐
7. lim
𝑥→𝑐
[f(x)
-
f(x) - lim
g(x)
[f(x)
g(x)]
𝑥→𝑐
.
f(x) - lim
𝑥→𝑐
lim
𝑓(𝑥)
𝑥→𝑐
=
𝑔(𝑥)
n
lim
𝑥→𝑐
8. lim
f(x) = [lim
9. lim
n
𝑥→𝑐
𝑥→𝑐
g(x)]
𝑥→𝑐
√𝑓(𝑥)
=
=
g(x)
𝑓(𝑥)
𝑔(𝑥)
f(x)]n
=
n
√lim 𝑓(𝑥)
b. Jika f suatu fungsi polinom atau
fungsi rasionalmaka,
lim f(x) =f(c)
𝑥→𝑐
Asalkan dalam kasus fungsi
rasional nilai penyebut c tidak
nol.
c. Andaikan f,g dan h adalah
fungsi yang memenuhi f)x) ≤
g(x) ≤ h(x) untuk semua x
dekat c,kecuali mungkin di c .
jika,
lim f(x) lim h(x) = L
Gambar 2.8 Grafik fungsi kuadrat
2.4 Limit
2.4.1 Definisi
Limit merupakan suatu gagasan yang
membedakan kalkulus dari cabang-cabang
matematika lainnya sehingga kalkulus sering
didefinisikan sebagai pengkajian tentang limit.
Limit dikenal sebaga proses tak hingga. Dalam
kalkulus , limit ditulis dalam bentuk :
Lim f(x) = L
x→c
yang berarti bahwa bilaman x dekat tapi
berlaainan dengan c, maka f(x) dekat ke L.
𝑥→𝑐
𝑥→𝑐
2.5 Diferensial (Turunan)
2.5.1 Definisi
Turunan fungsi f adalah fungsi lain
f’(dibaca “f aksen”) nilainya pada sembarang
bilangan c adalah :
𝑓(𝑥)−𝑓(𝑐)
f’(c) = lim
, asalkan limit ini ada .
𝑥−𝑐
2.4.2 Teorema tentang limit
Untuk memudahkan dalam penyelesaian
masalah limt, maka digunakan teoremateorema tentang limit. Teorema-teorema
tersebut adalah sebagai berikut.
a. Andaikan n bilangan bulat positif, k
konstanta, dan f dan g adalah fungsifungsi yang mempunyai limit di c maka,
1. lim k = k
𝑥→𝑐
maka dikatakan bahwa f terdefenisialkan
(terturunkan) di c . Pencarian turunan disebut
pendiferensilan, dan bagian kalkulus yang
berhubungan dengan turunandisebut kalkulus
diferensial.
2.5.2 Aturan Pencarian Turunan
Turunan dapat ditentukan tanpa proses
limit. Untuk itulah dirancang beberapa
teorema tentang turunan. Turunan suatu fungsi
f adalah fungsi lain f’. Misalkan rumus untuk
f(x) = x2 maka f’(x)=2x.
Beberapa teorema yang sering digunakan
dalam proses perhitungan turunan yaitu:
a. Aturan fungsi konstanta
𝑥→𝑐
2. lim
x=c
3. lim
k.f(x)= k.lim
4. lim
[f(x)
𝑥→𝑐
𝑥→𝑐
𝑥→𝑐
lim
𝑥→𝑐
𝑥→𝑐
f(x)
+
g(x)]
f(x) + lim
g(x)
𝑥→𝑐
𝑥→𝑐
Maka,
lim g(x) = L
=
27
Sudi Suryadi
b.
c.
d.
e.
f.
g.
h.
i.
J. Informatika AMIK-LB Vol.2 No.1/Januari/2014
jika f(x)= k dengan k suatu konstanta
maka untuk sembarang x, f(x) = 0
Aturan fungsi identitas
Jika f(x)=x, maka
f(x) 1
Aturan pangkat
Jika f(x)=xn, dengan n bilangan-bilangan
bulat positif maka f(x) = n.xn-1
Aturan kelipatan konstanta
Jika k konstanta dan f suatu fungsi yang
terdiferensialkan, maka
(kf)’(x)= k . f’(x)
Aturan jumlah
Jika
f
dan
g
fungsi-fungsi
terdiferensialkan, maka
(f + g)’(x) = f’(x) + g’(x).
Aturan selisih
Jika
f
dan
g
fungsi-fungsi
terdiferensialkan, maka
(f - g)’(x) = f’(x) - g’(x).
Aturan hasil kali
Andaikan f dan g fungsi-fungsi yang
dapat terdiferensialkan, maka
(f . g)’(x) = f’(x) . g’(x)+ g’(x). f’(x)
Aturan hasil bagi
Andaikan f dan g fungsi fungsi yang
dapat didiferensialkan dengan g(x) ≠ 0
𝑓
f’(x) .g’(x) + g’(x) .f’(x)
Maka, (𝑔) (𝑥) =
𝑔2(𝑥)
Andaikan g suatu fungsi yang dapat
diiferensialkan dan r suatu bilangan
rasional yang bukan -1 , maka
0≤𝑥≤1
= 1,2, … n, kemudian buat persegi panjang
dengan ukuran alas = ∆xi = xi –xi-1 dan tinggi f
(ci) = ci∈ [xi-1 , xi].
Luas persegi panjang ke-I pada gambar
berikut adalah ∆𝐿i= f(ci) . ∆xi sehingga luas
daerahA yang dihampiri oleh n sebuah persegi
panjang adalah :
Luas A ≈ ∑𝑛𝑖−1 𝑓(𝑐i). ∆xi
2.6 Integral tak tentu dan integral tentu
2.6.1 Integral tak tentu
Anti
penurunan
adalah
juga
mengintegralkan. Dalam lambang ∫ f(x) dx,
∫ disebut tanda integral dan f(x) disebut
integran. Jadi, dengan mengintegralkan
integral akan didapatkan integral tak tentu .
Beberapa aturan yang sering dipakai dalam
penyelesaian masalah anti turunan adalah
sebagai berikut :
a. Aturan pangkat
Jika r adalah sembarang bilangan
rasional keciali -1,maka
x r−1
∫ 𝑥 r dx = 𝑟+ 1 + C
b.
c.
d.
e.
[g(x)]
[g(x)rg’(x) dx = 𝑟+ 1 r+1+ C
Dengan menganggap u = g’(x) dx
sehingga aturan diatas menjadi,
u
∫ urdu = 𝑟+ 1r+1 + C
2.6.2 Integral tentu
Newton dan Leibniz keduanya
memperkenalkan versi yag dini dari konsep
ini. Tetapi Reimann yang memberi definisi
modern. Sekarang, anggap sebuah fungsi f
didefinisikan pada selang tutup [a, b] yang
boleh bernilai positif ataupun negative pada
selang tersebut dan bahkan tidak perlu
kontinu. Anggap suatu partisi P dari selang
tertutup [a, b] menjadi n selang bagian
memakai titik a=x0< x1 < x2 < x3< … < Xn-1<
Xn = b. panjang selangnya ∆xi = xi – xi-1
panjang partisi P ditulis |P| didefiniikan
sebagai |P| = max ∆xi. pilih ci∈ [xi-1 , xi], I
∫
Gambar 2.9 Jumlah Riemann ditafsirkan
jumlah aljabar dari luas lebih lanjut
∑𝑏𝑎 𝑓(𝑥)𝑑𝑥 disebut integral tentu (atau integral
Riemann ) f dari a ke b, Sehingga
𝑏
∫𝑎 𝑓(𝑥)𝑑𝑥 = lim ∑𝑛𝑖=1 𝑓(𝑐i) ∆xi
pada
|𝑃|→0
𝑏
penulisan ∫𝑎 𝑓(𝑥)𝑑𝑥; 𝑓(𝑥), 𝑎, 𝑏 berturut-
turut dinamakan integran , limit bawah dan
limit atas dari integral tertentu.
Sifat-sifat dari integral tentu adalah sebagai
berikut :
1. Sifat penambahan selang .
Jika f fungsi kontinu dalam sebuah
selang tutup yang mengandung tiga
𝑐
titik a, b dan c maka :∫𝑎 𝑓(𝑥)𝑑𝑥 =
∫ k.f(x) dx = k. ∫ f(x) dx
∫ [f(x) + g(x)] dx = ∫ f(x) dx + ∫ g(x) dx
∫ [f(x) - g(x)] dx = ∫ f(x) dx - ∫ g(x) dx
Aturan pangkat yang diperumum.
𝑏
𝑐
∫𝑎 𝑓(𝑥)𝑑𝑥 + ∫𝑏 𝑓(𝑥)𝑑𝑥
28
Sudi Suryadi
J. Informatika AMIK-LB Vol.2 No.1/Januari/2014
2. Sifat pembandingan
3. Jika f dan g diintegralkan pada [a,
b] dan jika f(x) ≤ g(x) untuk semua
x dalam [a, b], maka:
𝑐
M (b-a) ≤ ∫𝑎 𝑓(𝑥)𝑑𝑥 ≤ 𝑀(𝑏 − 𝑎)
4. Pendiferensial suatu integral tentu.
Andaikan f kontinu pada selang
tertutup [a, b] dan andaikan x
sebuah titik (variable) dalam [a,
b],maka:
𝑏
Dx[∫𝑎 𝑓(𝑡)𝑑𝑡 = f(x)
5. Teorema nilai rata-rata untuk
integral .
Jika f kontinu pada [a, b], maka
terdapat suatu bilangan c antara a
dan b sedemikian sehingga
𝑏
:∫𝑎 𝑓(𝑡)𝑑𝑡 = 𝑓(𝑐)(𝑏 − 𝑎)
6. Teorema simetri
Jika
fungsi
genap,maka
𝑎
𝑏
:∫−𝑎 𝑓(𝑥)𝑑𝑥 = ∫0 𝑓(𝑥)𝑑𝑥
Jika fungsi
ganjil, maka:
𝑎
∫−𝑎 𝑓(𝑥)𝑑𝑥 = 0
7. Jika f periode dengan periode p ,
𝑏+𝑝
𝑏
maka : ∫𝑎+𝑝 𝑓(𝑥)𝑑𝑥 = ∫𝑎 𝑓(𝑥)𝑑𝑥
metode cakram. Cara kerja dari metode ini
adalah sebagai berikut :
1.
Misalkan diketahui suatu fungsi y=f(x)
yang diputar terhadap sumbu x.
Gambar 2.10 Perputaran aebuah parabola
terhadap sumbu x.
2. Diambil Sepotong (sebagian) dari benda
putar tersebut. Misalkan diambil potongan
pada nilai x sehingga nilai fungsinya
adalah y.
2.6.3 Volume Benda Putar
Integral tentu dapat digunakan untuk
menghitung luas.ini tidak mengherankan
karena integral diciptakan untuk keperluan itu
.akan tetapi, integral juga banyak digunakan
untuk persoalan lainnya. Hamper tiap besaran
yang dapat dianggap sebagai hasil pemotongan
sesuatu menjadi bagian-bagian yang lebih
kecil. Aproksimasi tiap bagian ,penjumlahan
dan pengambilan limit apabila tiap bagian
mengecil, dapat diartikan sebagai suatu
integral.
Apabila sebuah daerah rata, yang
terletak seluruhnya pada satu bidang yang
terbagi oleh sebuah garis lurus tetap, diputar
melalui garis tersebut. daerah tersebut akan
membuat sebuah benda putar, garis yang tetap
tersebut dinamakan sumbu putar.
Misalkan beberapa cara yang digunakan
untuk mencari volume benda putar ini . salah
satu caranya adalah dengan menggunakan
Gambar 2.11 Potongan benda putar
3. Karena potongan tersebut berbentuk
silinder (taabung) maka untuk mencari
volume dari potongan tersebut dapat
digunakan rumus volume silinder. Sesuai
gambar diatas, maka jari-jari silinder
aaadalah sama dengan y dan tinggi dari
silinder adalah sama dengan selisih dari
nilai pada sumbu x yaitu nilai b dikurangi
nilai
a,sehingga volumenya dapat
dirumuskan sebagai berikut :
29
Sudi Suryadi
J. Informatika AMIK-LB Vol.2 No.1/Januari/2014
∆𝑉 = 𝜋𝑟 2t = 𝜋𝑦2∆x = 𝜋y2(x2-x1)
4. Sehingga rumus untuk mencari volume
benda putar adalah :
𝑏
𝑉 = ∫𝑎 𝜋y2 dx
Dengan
melakukan
sedikit
modifikasipada rumus diatas, maka rumus
untuk mencari volume pada benda putar untuk
sebuah fungsi kurva dengan menggunakan
integral tertentu yaitu :
a. Perputaran terhadap sumbu x(y=f(x))
Gambar 2.14 (a) perputaran dua fungsi
parabola terhadap sumbu x
Gambar 2.12 perputaran sebuah fungsi
terhadap sumbu x
𝑏
𝑉 = 𝜋 ∫𝑎 y2 dx
b. Perputaran terhadap sumbu y(x=f(y))
Gambar 2.14 (ab) Potongan benda putar untuk
gambar 2.14(a) diatas
Untuk mencari potongan benda diatas, dapat
digunakan rumus perhitungan volume silinder
kecil.
∆V1= 𝜋𝑟2t = 𝜋y12∆𝑥
∆V2= 𝜋𝑟2t = 𝜋y22∆𝑥
∆V=∆V2-∆V1= 𝜋y22− 𝜋y12∆𝑥 = 𝜋(y22- y12) ∆𝑥
𝑏
𝑉 = ∫𝑎 𝜋(y22- y12) dx atau V = |V2 – V1|
Dengan melakukan sedikit perubahan pada
rumus diatas, maka rumus untuk mencari
volume benda putar untuk dua fungsi
menggunakan integral yaitu,
a. Perputaran terhadap sumbu x
Gambar 2.13 perputaran sebuah fungsi
terhadap sumbu y
𝑏
𝑉 = 𝜋 ∫𝑎 x2 dy
Ada kalanya apabila sebuah benda
putar dipotong tegak lurus pada sumbu
putarnya, maka akan diperoleh sebuah cakram
yang ada lubangnya ditengahnya. Daerah
demikian disebut cincin,sehingga metoda
untuk mencari volume benda putar tersebut
disebut motoda cincin.
30
Sudi Suryadi
J. Informatika AMIK-LB Vol.2 No.1/Januari/2014
Gambar 2.15 Perputaran dua buah fungsi
terhadap sumbu x
𝑏
𝑉 = 𝜋 ∫𝑎 𝜋(y22- y12) dx atau V = |V2 – V1|
b. Perputaran terhadap sumbu y
4. Perhitungan volume benda putar yang
dihasilkan
Dalam tahapan ini, fungsi yang di-input akan
dimasukkan kedalam fungsi integral dengan
batasan yang telah di-input sebelumnya. Agar
lebih jelas mengenai proses kerja tersebut,
perhatikan contoh berikut ini. Misalkan
diketahui sebuah fungsi : Y =X2 + 2X + 1
dengan batasan mulai dari -5 sampai 5 maka
grafik fungsi akan diputar terhadap sumbu x
dan menghasilkan putaran berikut ini:
Gambar 2.16 perputaran dua buah fungsi
terhadap sumbu y
𝑏
𝑉 = 𝜋 ∫𝑎 𝜋(x22- x12) dys atau V = |V2 – V1|
II. PEMBAHASAN
DAN
PERANCANGAN
3.1 Pembahasan
Perangkat lunak penerapan fungsi ntegral
tentu menghitung volume benda putar yang
memiliki proses kerja sebagai berikut :
1. Inputfungsi
Fungsi yang di-input maksimal dua buah
dan berupa fungsi persamaan kuadrat
dengan satu variable. Dalam tahapan ini
juga harus ditentukan jenis perputaran
kurva yaitu terhadap sumbu x dan sumbu
y.
2. Input batas perputaran kurva
Dalam tahapan ini ditentukan batas-batas
kurva yang akan dilakukan perputaran.
3. Penggambaran grafik fungsi
Fungsi yang di-inputakan digambarkan
dalam diagram cartesius. Koordinat
cartesius
digambarkan
dengan
menggunakan skala. Sumbu x dan y
digambarkan dengan menggunakan skala
tersendiri. Skala tersebut diatur sesuai
dengan fungsi yang digambarkan.
Tujuan dari pembuatan skala ini adalah
untuk memperbesar grafik fungsi yang
akan digambarkan
Gambar 3.1 Benda putar hasil perputaran
grafik fungsi Y=X2 + 2X + 1
Volume benda putar yang dihasilkan adalah :
= ∏ ∫ (Y12)2 dx
= ∏ ∫ (x2 + 2 x+1)2dx
= ∏ ∫ (x2 + 2 x+1)(x2 + 2 x+1)2dx
= ∏ ∫ (x4 + 2x3 + x 2 + 2x 3 +4x2 +2x + x2+ 2
x+1)2dx
Volume benda putar yang dihasilkan adalah :
Volume benda putar I
= ∏ ∫ (Y12)2 dx
=∏ ∫ (x2 + 2 x+1)2dx
=∏ ∫ ( x 2 + 2 x+1) ( x 2 + 2 x+1)dx
=∏ ∫ (x4 + 2x3 + x 2 + 2x 3 +4x2 +2x + x2+ 2
x+1)2dx
=∏ ∫ (x4 + 4x3 + 6x 2 + 4x + 1)2dx
=∏ ∫ (0,2x2 + x4 + 2x3 +2x2+ x) untuk X1 = 5 sampai dengan X2 =5 =∏ ∫ |(1555) −
(−205)|
= 1760 ∏ satuan volume
Volume benda putar II
= ∏ ∫ (Y22)2 dx
=∏ ∫ (2x2 + x+1)2dx
=∏ ∫ (2x2 + x+1) (x2 + x+1)dx
31
Sudi Suryadi
J. Informatika AMIK-LB Vol.2 No.1/Januari/2014
=∏ ∫ (4x4 + 2x3 +2x 2 + 2x 3 +x2 +x + 2x2+
x+1)dx
=∏ ∫ (4x4 + 4x3 + 5x 2 + 2x+1)dx
=∏ ∫ (0,8x5 + x4 + 1,67x3 + x2+ x) untuk X1=
-5 sampai dengan X2=5
=∏ |(363.3) − (2063.33)|
= 5426.66 ∏ satuan volume
Volume benda putar
= |volume benda putar II – volume benda
putar I|
=|5426.67 ∏ - 1760∏ |
= 3666.67 ∏ satuan volum
Contoh perputaran grafik fungsi
terhadap sumbu y dapat dilihat pada
contoh berikut ini :
Misalkan diketahui sebuah fungsi : X
=Y2 + 3Y +2dengan batasan mulai dari
-2 sampai 5, maka grafik fungsi akan
diputar terhadap sumbu y dan
menghasilkan benda putar berikut ini :
Contoh lainnya :
Misalkan diketahui dua buah fungsi : X = Y2 +
3Y +2 dan X + 2Y + 1dengan batasan mulai
dari -2 sampai 5,maka grafik fungsi akan
diputar
terhadap
sumbu
Y
dengan
menghasilkan benda putar berikut ini:
Gambar 3.4 benda putar hasil perputaran
grafik fungsi X=Y2 +3Y +2 dan X = 2Y+1
Volume benda putar yang dihasilkan adalah :
Volume benda putar I
= ∏ ∫ (X12)2 dy
=∏ ∫ (Y2 + 3Y+2 )2dy
=∏ ∫ (Y2 + 3Y + 2) (Y2 + 3Y + 2)dy
=∏ ∫ (Y4+ 3Y3 +2Y 2 + 3Y 3 + 9Y2 + 6Y +
2Y2+ 6Y + 4)dy
=∏ ∫ (Y4 + 6Y3 + 13Y 2 + 12Y+4)dy
=∏ ∫ [0,2y5 + 1.5y4 + 4.33y3 + 6y2+ 4y]
untuk Y1= -2 sampai dengan Y2=5
=∏ |(221.67) − (−4.67)|
= 226.32 ∏ satuan volume
Volume benda putar
= |Volume benda putar II – Volume benda
putar I|
=|226.33 ∏ −2275.23 ∏
=2048.9 ∏ satuan volume
3.2 Perancangan
Perangkat lunak penerapan fungsi integral
tentu untuk menghitung volume benda
putar
ini
dirancang
dengan
menggunakan Microsoft xisual basic 6.0.
perancangan perangkat lunak ini dapat
dibagi menjadi dua abagian yaitu
perancangan menu dan perancangan
form.
3.2.1 Perancangan menu
Gambar 3.3 Benda putar hasil perputaran
grafik fungsi X = Y2+3Y+2
Volume benda putar yang dihasilkan adalah :
Volume benda putar I
= ∏ ∫ (X12)2 dy
=∏ ∫ (Y2 + 3 x+2)2dy
=∏ ∫ ( Y2 + 3x+2) ( Y2 + 3Y+ 2)dy
=∏ ∫ (Y4 + 3Y3 + 2Y 2 + 3Y 3 + 9Y2 +6Y +
2Y2+ 6Y+4) 2dy
=∏ ∫ (Y4 + 6Y3 + 13Y 2 + 12Y +4 )2dx
=∏ ∫ (0,2Y2 + 1.5Y4 + 4.33Y3 +6Y2+ 4Y)
untuk Y1 = -2 sampai dengan Y2 =5
=∏ ∫ |(274.17) − (−1.07)|
= 2275.24 ∏ satuan volume
32
Sudi Suryadi
J. Informatika AMIK-LB Vol.2 No.1/Januari/2014
menu yang diranang dari perangkat lunak ini
adalah sebagai berikut :
4. Label,untuk menampilkan keterangan
program stui dan nama kampus.
5. Timer,sebagai control yang digunakan
untuk masuk ke form selanjutnya.
3.2.2.2 Form menu
Form menu merupakan form utama
dari program. Form ini merupakan media
interface user untuk memilih menu-menu yang
tersedia pada program. Rancangan form menu
diperlihatkan pada gambar berikut:
3.2.2 Perancangan form
Form-form yang terdapat dalam perangkat
lunak ini,yaitu:
1. From splash screen
2. Form menu
3. Form input fungsi
4. Form penggambaran grafik fungsi
5. Form perhitungan volume
6. Form pengaturan grafik
7. From about
Gambar 3.6 Rancangan form menu
Keterangan :
1. Commondialo,untuk membuka kotak
dialog save / open
2. Menu bar,merupakan menu utama
yang dirancang untuk setiap program
aplikasi. Pada menu bar ini terdapatt
beberapa menu antara lain:
a. File dengan sub-sub menu :
i.
Buka,untuk membuka file
yang telah disimpan dan
memasukkan isi file ke dalam
textbox.
ii.
Simpan,untuk menyimpan isi
textbox kedalam sebuah file
data
iii. Keluar, untuk menutup form
menu dan keluar dari program
.
b. Persaan Grafik Fungsi,dengan subsub menu :
i.
Input
fungsi,
untuk
menampilkan form input
fungsi
ii.
Grafik
fungsi,
hasil
perhitungan
volume,untuk
menampilkan
form
penggambaran grafik fungsi
3.2.2.1 Form splash screen
Form splash screen merupakan from
yang pertama kali muncul pertama kali pada
saat program dijalankan. Rancangan form
splash screen diperlihatkan pada gambar
berikut :
Gambar 3.5 Rancangan From splash screen
Keterangan :
1. Label,untuk menampilkan judul topic
tugas akhir .
2. Label,untuk menampilkan keterangan
nama dan nim perancang perangkat lunak.
3. Image,untuk menampilkan gambar icon
dari perangkat lunak .
33
Sudi Suryadi
J. Informatika AMIK-LB Vol.2 No.1/Januari/2014
iii.
Hasil perhitungan volume.
Untuk menampilkan form
perhitungan volume
iv. Export grafik dan hasil
perhitungan Ms.word,untuk
mengekspor grafik dan hasil
perhitungan ke Microsoft
word .
c. Pengaturan, untuk menampilkan
form pengaturan Grafik.
d. Tentang, untuk menampilkan from
about.
3.2.2.3 From input fungsi
From Input fungsi merupakan form pertama
setelah form menu yang harus diinput untuk
mendapatkan nilai fungsi. Rancangan form
input fungsi diperlihatkan pada gambar berikut
:
b. textbox, sebagai tempat penginputan
nilai konstanta yang diinginkan.
c. RichTextBox,
sebagai
tempat
keterangan dari persamaan kuadrat
setelah konstanta dimasukkan.
3. ComandButton
‘OK’,
untuk
menyimpan data hasil input ke dalam
memori dan kembali ke form menu.
4. CommandButton
‘Batal’
untuk
membatalkan input data.
5. CommandButton
‘Keluar’
untuk
menutup form input fungsi dan kembali
ke form menu.
3.2.2.4 Form penggambaran grafik fungsi
Form penggambaran grafik fungsi
digunakan untuk menampilkan gambar dari
fungsi yang telah diinput pada from input
fungsi. Rancangan form penggambaran grafik
fungsi diperlihatkan pada gambar berikut :
Gambar 3.8 Rancangan Form Penggambaran
grafik fungsi.
Keterangan :
1. PictureBox, untuk daerah penggambaran
grafik fungsi.
2. RichTextBox, untuk daerah tampilan
besar volume benda putar.
3. Shape, sebagai keterangan dari proses
penggambaran dan legenda dari gambar
grafik fungsi
4. progressBar,
untuk
menampilkan
lamanya proses kerja penggambaran
grafik fungsi.
5. Timer, mengatur pergerakan dari
progress bar
6. CommandButton
‘Gambar’,
untuk
menggambar ulang grafik fungsi.
7. commandButton
‘Stop’,
untuk
menghentikan proses penggambaran\
Gambar 3.7 Rancangan form input fungsi .
Keterangan :
1. OptionButton, untuk memilih jenis
perputaran yang diinginkan.
2. Frame, merupakan daerah penginputan
data untuk fungsi kurva dengan
perputaran terhadap sumbu yang
diinginkan. Didalam frame terdapat
beberapa
toolbox
yang
digunakan,seperti:
a. CheckBox, untuk memilih banyaknya
fungsi yang akan dilakukan.
34
Sudi Suryadi
J. Informatika AMIK-LB Vol.2 No.1/Januari/2014
8. CommandButton
‘keluar’,untuk
menutup form penggambaran grafik
fungsi dan kembali ke form menu
3.2.2.5 Form perhitungan volume
Form perhitungan volume digunakan
untuk menampilkan hasil perhitungan dari
fungsi yang telah diinput pada form input
fungsi. Rancangan form perhitungan volume
diperlihatkan pada gambar berikut :
Gambar 3.10 Rancangan form pengaturan
grafik.
1. PictureBox, untuk pengaturan warna
grafik
2. CommandButton’Default’
,
untuk
mengatur warna kembali seperti semula /
warna standart yang telah ditentukan.
3. CommandButton’Simpan’,
untuk
menyimpan perubahan warna grafik
4. CommandButton’Keluar’,
untuk
menutup form pengaturan grafik dan
kembali ke form menu.
Gambar 3.9 Rancangan Form Perhitungan
Volume
Keterangan :
1. RichTextBox, untuk daerah tampilan
hasil perhitungan.
2. CommandButton
‘Hitung’
untuk
menghitung ulang volume benda putar.
3. CommandButton’Keluar’,
untuk
menutup form perhitungan volumedan
kembali ke form menu.
3.2.2.7 Form about
Form
about
digunakan
untuk
meenampilkan tentang nama perancang dan
judul dari perancangan. Rancangan about
diperlihatkan pada gambar berikut :
3.2.2.6
Form pengaturan grafik
Form pengaturan grafik digunakan
untuk mengatur tampilan warna grafik.
Rancangan formpengaturan grafik dapat
diperlihatkan pada gambar berikut:
Gambar 3.11 Rancangan Form about
Keterangan :
1. Label,untuk menampilkan judul topic
tugas akhir .
2. Label,untuk menampilkan keterangan
nama dan nim perancang perangkat
lunak.
35
Sudi Suryadi
J. Informatika AMIK-LB Vol.2 No.1/Januari/2014
3. Image,untuk menampilkan gambar
icon dari perangkat lunak .
4. Label,untuk menampilkan keterangan
program stui dan nama kampus.
5. Commandbutton‘OK’ untuk menutup
form about dan kembali ke form menu
6. CommandButton
‘Teori’,
untuk
menampilkan teori yang berhubungan
dengan integral tentu.
IV.ALGORITMA DAN IMPLEMENTASI
4.1
Algoritma
Algoritma perancangan peangkat lunak
penerapan fungsi integral tentu untuk
menghitung isi benda putar yang dibentuk
dari perputarankurva menjadi dua bagian
yaitu :
1. Algoritma penggambaran grafik,dibagi
menjadi tiga bagian, yaitu :
a. Algoritma perhitungan skala untuk
sumbu X dan Y.
b. Algoritma penggambaran grafik fungsi
c. Algoritma pengarsiran batas daerah
perputaran kurva
2. Algoritma perhitungan besar isi benda
putar dengan fungsi integral tentu
suatu daerah grafik,penulis merancang
algoritma perhitungan skala untuk sumbu X
dan Y .
algoritma
perhitungan
skala
menghitung besar skala untuk sumbu x dan y
sedemikian rupa hingga persamaan kurva yang
di input dapat digambarkan dengan baik pada
daerah grafik yang telah ditentukan.
Algoritma perhitungan skala untuk
sumbu x dan y adalah sebagai berikut :
1. Menghitung titik puncak parabola
dengan rumus (-b / 2a).
Jika P1.A <> 0 Maka
(X=-B/2a)
Temp1 = Round (-P1.B
/ (2 * P1.A), 2)
Jika Temp1 < Min1
maka Min1 = Temp1
Jika Temp1 < Max1
maka Max1 = Temp1
(Y = -(b^2–(4ac))/(4a)))
Temp1 = -bagi ( ( ( P1.
B ^ 2) – (4 * P1.A * P1.C)),
Jika Temp1 < Min2
maka Min2 = Temp1
Jika Temp1 < Max2
maka Max2 = Temp1
End Jika
Algoritma diatas diulang untuk
fungsi yang kedua
4.1.1 Algoritma penggambaran grafik
Algoritma ini digunakan untuk
menghitung skala sumbu X dan sumbu Y,
menggambar grafik fungsi dan memberi
arsiran pada daerah perputaran sesuai dengan
fungsi yang di-input. Pada intinya,algoritma
menggambarkan
grafik
dengan
cara
menggambar piksel peer piksel pada posisi
koordinat tentu yang akan membentuk satu
grafik fungsi.
2. Menghitung nilai fungsi dengan
nilai substitusi batas atas dan batas
bawah.
Jika B1 < Min1 maka Min1= B1
Jika B1 > Max1 maka Max1= B1
4.1.1.1 Algoritma
perhitungan
skala
untuk sumbu X dan sumbu Y
Pada penggambaran grafik,terdapat
input fungsi dengan nilai variabel (a, b, c)
yang bervariasi,dari nilai kecil hingga nilai
besar. Input dengan nilai variabel dan batas
daerah yang relative kecil hanya memerlukan
daerah (space) penggambaran yang kecil,
tetapi input dengan nilai variabel dan batas
daerah yang relatif besar memerlukan daerah
(sapce) penggambaran yang besar. Untuk
dapat menggambar grafik fungsi dengan nilai
variabel yang relative besar pada suatu pada
Jika B2 < Min1 maka Min1= B2
Jika B2 > Max1 maka Max1= B2
(Nilai substitusi untuk fungsi)
Jika P1.aktif maka
‘Y=ax2+ bx + c ↔ B1
Templ = (P1.A * (B1 ^
2))+(P1.B * B1)+(P1.C)
Jika Templ < Min2
maka min2 = Templ
Jika Templ > Max2
maka Max2 = Templ
‘Y=ax2+ bx + c ↔ B2
36
Sudi Suryadi
J. Informatika AMIK-LB Vol.2 No.1/Januari/2014
Templ = (P1.A * (B2 ^
2))+(P1.B * B2)+(P1.C)
Jika Templ < Min2
maka min2 = Templ
Jika Templ > Max2
maka Max2 = Templ
End Jika
End jika
4.1.1.2 Algoritma penggambaran grafik
fungsi
Algoritma Penggambaran grafik fungsi
melakukan penggambaran
grafik sesuai
dengan fungsi yang di-input. Prosedur
penggambaran dari algoritma ini adalah
melakukan test point (tes titik) dengan
menggunakan rumus berupa fungsi yang di
kurang input untuk menghasilkan posisi
penempatan piksel, nilai posisi penempatan
piksel kemudian dikalkulasikan dengan skala
yang telah dihasilkan sebelumnya untuk
mendapatkan nilai posisi representatif pada
daerah
sketsa.
Setelah
nilai
posisi
representative
dihasilkan,
Algoritma
menggambar satu piksel pada posisi tersebut
pada daerah sketsa. Penggambaran piksel
dilakukan beulangkali hingga didapat suatu
grafik fungsi
Algoritma penggambaran grafik fungsi
adalah sebagai berikut,
1. Menggambar grafik fungsi I dari posisi :
b1 – Abs(2 * b1) hingga b2+ Abs(2 *
b2).(b1=nilai batas yang paling kecil, b2 =
nilai batas yang paling besar).
With P1
Jika . Aktif maka
(Gambar dari nilai templ)
Templ= IIf(B1<=B2,B1,B2)
Templ= Templ – Abs (2 * Templ)
(Cek apakah keluar dari daerah
penggambaran)
If strperputaran = “x”Then
If Templ <- SkalaX Then
Templ =-SkalaX
End If
Else
(Nilai substitusi untuk fungsi II)
Jika P2.aktif maka
‘Y=ax2+ bx + c ↔ B1
Templ = (P2.A * (B1 ^
2))+(P2.B * B1)+(P2.C)
Jika Templ < Min2
maka min2 = Templ
Jika Templ > Max2
maka Max2 = Templ
‘Y=ax2+ bx + c ↔ B1
Templ = (P2.A * (B2 ^
2))+(P2.B * B2)+(P2.C)
Jika Templ < Min2
maka min2 = Templ
Jika Templ > Max2
maka Max2 = Templ
3. Mengambil nilai maksimum x dan
y yang didapatkan dari fungsi dari
batas bawah hingga batas atas
Max1 = IIf (Abs (Max1) > Abs
(Min1),Abs (Max1), Abs(Min1))
Max2 = IIf (Abs (Max2) > Abs
(Min2),Abs (Max2), Abs(Min2))
4. Kalikan nilai maksimum x dan y
yang didapat sebesar 1,4+1,
sehingga gambar grafik masih
terdapat space (jarak) dibagian atas
dan samping.
Jika Strperputaran =”x”maka
SkalaX = Round (Max1
* 1.4) + 1
SkalaY = Round (Max2
* 1.4) + 1
Jika tidak, maka
SkalaX = Round (Max2
* 1.4) + 1
SkalaY = Round (Max1
* 1.4) + 1
If Templ <- SkalaY Then
Templ =-SkalaY
End If
End If
(Gambaran sampai nilai temp2)
Temp2= IIf(B1>=B2, B1, B2)
Temp2= temp2 + Abs (2* temp2)
37
Sudi Suryadi
(Cek
apakah
keluar
penggambaran)
If strperputaran = “x”temp
If Temp2 > SkalaX Then
Temp2 = SkalaX
End If
Else
J. Informatika AMIK-LB Vol.2 No.1/Januari/2014
dari
Jika (Round(x, 2 <> Round(Temp1, 2))
daerah
Maka
PictGrafik.Line (X1, y)- (X2, Y2),_
(Delay Sebentar)
Jika bDoEvents Maka
DoEvents
End Jika
(Nilai Piksel sebelumnya)
X2 = X1
Y2 = y
Wend
End jika
End With
If Temp2 > SkalaY Then
Temp2 = SkalaY
End If
Else
(Selisih penggambaran antar piksel)
nInc = Round (Abs(temp2- temp1)/ 3000 , 5)
x = temp1-nInc
(Set Progress bar value = 0)
Bar . value = 0
Bar. Max = bagi((temp2-x),nInc)+1
(Mulai looping untuk penggambaran dari
batas temp1 ke temp2)
while x <temp2
(Tambah x)
x = x+nInc
(gerakan progress bar)
Bar.value = bar. Value+1
(Hitung nilai substitusi terhadap persamaan
garis dan nilai posisi (x1,y) sebagai
representasi posisi(x,y) pada daerah
penggambaran)
Jika strperputaran = “x” maka
(perputaran terhadap sumbu X)
X1 = MidX + (x * bagi (MidX ,
skalaX))
(Nilai Sustitusi Y)
y = - ( ( .A * (x ^ 2 ) ) + (.B * x) + .C)
y = MidY + ( y* Bagi (MidY, SkalaY))
Jika tidak, maka
(Perputaran terhadap sumbu y)
y = (MidY + ( -x * Bagi (MidY,
SkalaY)))
(Nilai substansi X)
X1 = ( ( .A * (x ^ 2 ) ) + (.B * x) + .C)
X1 = MidX + ( X1 * Bagi (MidX,
SkalaX))
End jika
(Gambar piksel pada posisi (xl, y))
PictGrafik.Pset (X1, y), Warna.Kurva1
(Gambar garis dari posisi Piksel
sekarang keposisi piksel sebelumnya)
2. Menggambar Fungsi II .
Algoritma ini sama dengan
algoritma di atas.
4.1.1.3 Algoritma Penggambaran batas
daerah perputaran kurva
Algoritma penggambaran batas daerah
kurva menggambarkan peta grafik dari fungsi
yang di-input dan memberikan arsiran pada
daerah yang dibatasi oleh fungsi yang akan
dicari besar volume putarnya. Peta dari grafik
yang terletak pada bidang putar yang
bersebrangan
dengan
bidang
grafik
sebenarnya adalah persamaan yang di-input
dikali -1 (Misalkan : persamaan garis y = ( 2x
+ 1) Memiliki peta grafik persamaan garisy
+-1 * (2x +1) atau y = -2x – 1)
Algoritma penggambaran batas daerah
perputaran kurva adalah sebagai berikut :
1. Menggambar peta grafik dari
fungsi I dari ats bawah hingga ata,
Daerah arsiran fungsi I dan gambar
elips utnuk grafik benda putar
(Counter untuk penggambaran
garis arsiran setiap 15 piksel)
Temp3 = 0
With P1
Jika .Aktif Maka
(Nilai batas yang kecil)
Temp1 = IIf (B1 <+ B2, B1, B2)
(Nilai batas yang besar)
Temp2 = IIf(B1 >= B2, B1, B2)
38
Sudi Suryadi
J. Informatika AMIK-LB Vol.2 No.1/Januari/2014
X2 = X1
Y2 = y
(Selisih penggambaran antar piksel)
nInc = Round(Abs(Temp2) / 300, 5)
x = Temp1 – nInc
Wend
(Gambar ellips untuk perputaran
fungsi I)
Jika strperputaran = “X” Maka
(Gambar ellips utnuk batas-1)
Temp1 = MidX + (B1 * bagi
(MidX , skalaX))
Temp2 = ( ( .A * (B1 ^ 2 ) ) +
(.B * B1) + .C)
Temp2 = Round(Temp2 *
Bagi(MidY, SkalaY), 2)
PictGrafik.Circle
(Temp1,
MidY), Abs(Temp2), _
(Mulai
looping
penggambaran
penggambaran)
While x < Temp2
(Tambah x dan counter Temp3)
x = x + nInc
Temp3 = Temp3 + 1
(Hitung nilai substitusi terhadap persamaan
garis daan nilai posisi (x1,y) sebagai
representasi posisi(x,y) pada daerah
penggambaran)
Jika strperputaran = “X” Maka
(perputaran terhadap sumbu x)
X1 = MidX + (x * bagi (MidX ,
skalaX))
(Nilai substitusi Y)
y = - ( ( .A * (x ^ 2 ) ) + (.B * x) + .C)
y = MidY + ( y* Bagi (MidY, SkalaY))
(Nilai substansi X)
X1 = ( ( .A * (x ^ 2 ) ) + (.B * x) + .C)
X1 = MidX + ( X1 * Bagi (MidX,
SkalaX))
End jika
(Gambar piksel pada posisi (xl, y))
PictGrafik.Pset (X1, y), Warna.Kurva1
(Gambar garis dari posisi Piksel
sekarang keposisi piksel sebelumnya)
Jika (Round(x, 2 <> Round(Temp1, 2)) Maka
PictGrafik.Line (X1, y)- (X2, Y2),
Warna. Kurva1
(Gambar arsiran apabila fungsi -2 tidak
ada)
Jika P2 aktif = False And Temp3 Mod 15 = 0
Maka
Jika str perputaran = “X” Maka
PictGrafik.Line (X1, y)- (X2, Y2) MidY - _
(y
–
MidY)), Warna. Kurva1
Jika tidak, maka
PicrGrafik. Line (X1, y) – (MidX - _
(X1 – MidX )), y) , Warna kurava1
End Jika
End Jika
End Jika
(Nilai Sebelumnya)
Warna.Kurva1,0, 0, 10
(Gambar elips untuk batas -2)
Temp1 = MidX + (B2 * bagi (MidX , skalaX))
Temp2 = ( ( .A * (B2 ^ 2 ) ) + (.B *
B2) + .C)
Temp2 = Round(Temp2 * Bagi(MidY,
SkalaY), 2)
PictGrafik.Circle
(Temp1,
MidY),
Abs(Temp2), _
Warna.Kurva1,0, 0, 10
Jika tidak, maka
(Gambar ellips untuk batas-1)
Temp1 = MidY + (-B1 * bagi
(MidX , skalaX))
Temp2 = ( ( .A * (B1 ^ 2 ) ) +
(.B * B1) + .C)
Temp2 = Round(Temp2 *
Bagi(MidY, SkalaY), 2)
PictGrafik.Circle
(MidX,
Temp1), Abs(Temp2), _
Warna.Kurva1, 0, 0, 0.1
(Gambar ellips untuk batas-1I)
Temp1 = MidY + (-B1 * bagi
(MidY, skalaY))
Temp2 = ( ( .A * (B2 ^ 2 ) ) +
(.B * B2) + .C)
Temp2 = Round(Temp2 *
Bagi(MidY, SkalaY), 2)
PictGrafik.Circle
(MidX,
Temp1), Abs(Temp2), _
Warna.Kurva1, 0, 0, 0.1
End Jika
39
Sudi Suryadi
J. Informatika AMIK-LB Vol.2 No.1/Januari/2014
End Jika
End With
2. Menggambar fungsi II dan gambbar elips
untuk grafik benda putar. Algoritma ini
sama dengan algoritma di atas.
mempunyai spesifikasi minimal adalah sebagai
berikut:
1. Processor Intel Pentium I 300 Mhz.
2. Memori 64 MB.
3. Hardisk dengan free space minimal
300 MB
4. VGA card 1 MB dan minitor
dengan resolusi 1024 x 768 Piksel
Aplikasi ini adalah lingkungan system operasi
windows Me, 2000, XP Home dan XP Visual
Basic 6.0 dengan didukung oleh windows API.
4.2.2 Pengujian Program
Sebagai contoh, penulis meng-input
data sebagai berikut.
Contoh – 1 (fungsi berputar terhadap
sumbu x :
a. Fungsi I
: Y1 = X2 + 1
b. Fungsi II
: Y2 = X + 3
c. Batas Bawah (X1) = -1 batas atas (X2)
=2
d. Proses penggambaran grafik fungsi,
adalah sebagai berikut :
4.1.2 Algoritma perhitungan besar isi
benda putar dengan fungsi integral
tentu
Fungsi dari Algoritma ini adalah
menghasilkan nilai integral dari persamaan
dengan batas atas dan batas bawah yang telah
diinput . penulis merancang algoritma ini
dalam bentuk fungsi berikut :
(Batas bawah)
Hasil1 =
(0.2 * (A ^ 2) * (Batas1 ^ 5)) +
_
(0.5 * A * B *
(Batas1 ^ 4)) + _
(( 1 / 3) * ( 2 * A
* C) + (B ^ 2)) * (Batas1 ^ 3)) + _
(( B * C *
(Batas1 ^ 2)) + _
(( C ^ 2) *
Batas1)
(Batas Atas)
Hasil1 =
(0.2 * (A ^ 2) *
(Batas2 ^ 5)) + _
(0.5 * A * B *
(Batas2 ^ 4)) + _
(( 1 / 3) * ( 2 * A
* C) + (B ^ 2)) * (Batas2 ^ 3)) + _
(( B * C *
(Batas2 ^ 2)) + _
(( C ^ 2) *
Batas1)
(Fungsi Integral)
FgsIntegral = Round(Abs (Hasil2 –
Hasil1), 2)
-
4.2
Implementasi system
Implementasi system program ini
mencakup spesifikasi kebutuhan perangkat
keras (hardware) dan spesifikasi perangkat
lunak(software).
4.2.1 Spesifikasi perangkat keras dan
perangkat lunak
Program ini dijalankan dengan
menggunakan perangkat keras (hardware)yang
40
Gambar 4.1 Hasil penggambaran grafik
fungsi kuadrat dengan persamaan garis
Y1 = X2 + 1 dan Y2 = X
+ 3 dengan batas X1 = -1 dan X2 = 2
Tahapan perhitungan volume benda
putar yang ditampilkan oleh program
adalah sebagai berikut:
INPUT
Fungsi I
: X2 + 1
Fungsi II
:X+3
⟹dengan batas bawah (X1) = -1 dan
batas atas (X2) = 2
Volume benda putar I
= ∏ ∫ (Y1)2 dx
=∏ ∫ (x2+1)2dx
=∏ ∫ ( x 2 +1) ( x 2 +1)dx
=∏ ∫ (x4 + x 2 + x2 +1)2dx
=∏ ∫ (x4 + 2x 2 + 1)2dx
Sudi Suryadi
J. Informatika AMIK-LB Vol.2 No.1/Januari/2014
=∏ ∫ (0,2x5 + 0,67x3+ x)
untuk X1 = -1 sampai dengan
X2 =2 =∏ ∫ |(13.73) −
(−1.87)|
= 15.6∏ satuan volume
Volume benda putar II
= ∏ ∫ (Y2)2 dx
=∏ ∫ (x + 3)2dx
=∏ ∫ ( x + 3) (x+ 3)dx
=∏ ∫ (x 2 + 3x+3x+9)dx
=∏ ∫ (x 2 + 6x+9)dx
=∏ ∫ (0,33x3 +
x2+ 9x)
untuk X1= -1 sampai dengan
X2=2
=∏ |(32.67) − (−6.33)|
= 39∏ satuan volume
Volume benda putar
= |volume benda putar II –
volume benda putar I|
=|39 ∏ - 15.6 ∏ |
= 23.4∏ satuan volum
Contoh – 2(fungsi berputar terhadap
sumbu x):
a. Fungsi I : Y1 = X2 +2X + 1
b. Fungsi II : Y2 = 3X +2X + 3
c. Batas Bawah (X1) = -5 batas atas
(X2) = 7
d. Proses penggambaran grafik fungsi,
adalah sebagai berikut :
⟹dengan batas bawah (X1) = -5 dan
batas atas (X2) = 7
Volume benda putar I
= ∏ ∫ (Y1)2 dx
=∏ ∫ (x2+ 2X + 1)2dx
=∏ ∫ ( x 2 + 2X + 3) ( x 2 +
2X +3) dx
=∏ ∫ (x4 + 2x 3+ 3x2 +2x3+
4x2 + 6x+ 3x2 +6x +9)2dx
=∏ ∫ (x4 + 2x3 +10x2 +12x +
9)2dx
=∏ ∫ (0,2x5 + 4x3 +3,33x3+
6x2+ 9x) untuk X1 = -1 sampai
dengan
X2
=2
=∏ ∫ |(7262.7) −
(−311.67)|
= 7574.4∏ satuan volume
Volume benda putar II
= ∏ ∫ (Y1)2 dx
=∏ ∫ (3x2+ 2X + 4)2dx
=∏ ∫ ( 3x 2 + 2X + 4) ( 3x 2 +
2X +4) dx
=∏ ∫ (9x4 + 6x 3+ 12x2 +6x3+
4x2 + 8x+ 12x2 +8x + 16)2dx
=∏ ∫ (9x4 + 12x3 + 28x2
+16x + 16)2dx
=∏ ∫ (1,8x5 + 3x4 + 9,33x3+
8x2+ 16x) untuk X1 = -5
sampai
dengan
X2
=7
=∏ ∫ |(41160.93) −
(−4796.67)|
= 45957.6 ∏ satuan volume
Volume benda putar
= |volume benda putar II –
volume benda putar I|
=|45957.6 ∏ - 7574.4 ∏ |
= 3838.2 ∏ satuan volum
Contoh – 3 (Fungsi berputar terhadap
sumbu y ) :
a. Fungsi I
: X1 = 2Y2 +Y +
3
b. Fungsi II
: Y2 = Y2 +Y + 3
c. Batas Bawah (Y1) = -3 batas
atas (X2) = 3.
d. Proses penggambaran grafik
fungsi, adalah sebagai berikut :
Gambar 4.2 Hasil penggambaran grafik
fungsi kuadrat dengan persamaan garis
Y1 = X2 + 2X + 3 dan Y2 = 3X + 2X +
3 dengan batas X1 = -5 dan X2 = 7
Tahapan perhitungan volume benda putar yang
ditampilkan oleh program adalah sebagai
berikut:
FUNGSI :
- Fungsi I
: X2 + 2X + 3
- Fungsi II
: 3X2 + 2X + 4
41
Sudi Suryadi
J. Informatika AMIK-LB Vol.2 No.1/Januari/2014
=∏ ∫ (0,2Y5 + 0.5Y4 +
2.33Y3+ 3Y2+ 9Y) untuk Y1 =
-3 sampai dengan Y2 =3
=∏ ∫ |206.1 − (−71.1)|
= 277.2∏ satuan volume
Volume benda putar
= |volume benda putar II –
volume benda putar I|
=|277.2∏ - 676.8∏ |
= 399.6∏ satuan volum
Contoh – 4 (Fungsi berputar terhadap
sumbu y ) :
e. Fungsi I
: X1 = 2Y+ 1
f. Fungsi II
: Y2 = 5Y + 8
g. Batas Bawah (Y1) = 1 batas atas
(Y2) = 5.
h. Proses penggambaran grafik
fungsi, adalah sebagai berikut :
Gambar 4.3 Hasil penggambaran grafik fungsi
kuadrat dengan persamaan garis
X1 = 2Y2+ Y + 3 dan X2 = Y2 +Y + 3
dengan batas Y1 = -3 dan X2 = 3
Tahapan perhitungan volume benda putar yang
ditampilkan oleh program adalah ssebagai
berikut :
FUNGSI :
- Fungsi I
: 2Y2 + Y + 3
- Fungsi II
: Y2 + Y + 3
⟹dengan batas bawah (X1) = -5 dan
batas atas (X2) = 7
Volume benda putar I
= ∏ ∫ (X1)2 dy
=∏ ∫ (2Y2+ Y + 3)2dy
=∏ ∫ (2Y2+ Y + 3)(2Y2+ Y +
3)dy
=∏ ∫ (4Y4 + 2Y 3+ 6Y2
+2Y3+ Y2 + 3Y+ 6Y2 +3Y +
9)dy
=∏ ∫ (4Y4 + 4Y3 +13Y2 + 6Y
+ 9)2dy
=∏ ∫ (0,8Y5 + Y4 + 4,33Y3+
3Y2+ 9Y) untuk Y1 = -3
sampai
dengan
Y2
=3
=∏ ∫ |(446.4) − (−230.4)|
= 676.8∏ satuan volume
Volume benda putar II
= ∏ ∫ (X1)2 dy
=∏ ∫ (Y2+ Y + 3)2dy
=∏ ∫ (Y2+ Y + 3)(Y2+ Y +
3)dy
=∏ ∫ (Y4 + Y 3+ 3Y2 +Y3+ Y2
+ 3Y+ 3Y2 +3Y + 9)dy
=∏ ∫ (Y4 + 2Y3 +7Y2 + 6Y +
9)2dy
Gambar 4.4 Hasil penggambaran grafik fungsi
kuadrat dengan persamaan garis
X1 = 2Y+ 1 dan X2 = 5Y + 8 dengan
batas Y1 = 1 dan Y2 = 5
Tahapan perhitungan volume benda putar yang
ditampilkan oleh program adalah ssebagai
berikut :
FUNGSI :
- Fungsi I
: 2Y+ 1
- Fungsi II
: 5Y+ 8
⟹dengan batas bawah (Y1) = 1 dan
batas atas (Y2) = 5
Volume benda putar I
= ∏ ∫ (X1)2 dy
=∏ ∫ (2Y+ 1)2dy
=∏ ∫ (2Y+ 1)(2Y+ 1)dy
=∏ ∫ (4Y2 + 2Y + 1)dy
=∏ ∫ (4Y2+ 4Y+ 1)2dy
=∏ ∫ (1.33Y3 + 2Y2+Y)
untuk Y1 = 1 sampai dengan Y2
42
Sudi Suryadi
J. Informatika AMIK-LB Vol.2 No.1/Januari/2014
=
5=∏ ∫ |(221.67) −
(4.33)|
= 217.34∏ satuan volume
Volume benda putar II
= ∏ ∫ (X2)2 dy
=∏ ∫ (5Y+ 8)2dy
=∏ ∫ (5Y+ 8) (5Y+ 8) dy
=∏ ∫ (25Y2 + 40Y + 40Y +
64)dy
=∏ ∫ (25Y2+ 80Y+ 64)2dy
=∏ ∫ (8.33Y3 + 4Y2 +64Y)
untuk Y1 = 1 sampai dengan Y2
= 5 =∏ ∫ |(2361.67) −
(ℎ𝑢112.33)|
= 2249.34∏ satuan volume
Volume benda putar
= |volume benda putar II –
volume benda putar I|
=|2249.33∏ - 217.33∏ |
= 2032∏ satuan volum
5.2 saran
Adapun saran yang diberikan penulis
yaitu :
1. Perangkat lunak dapat dikembangkan
untuk fungsi kurva berorde lebih
besar dari dua dan fungsi integral lain
yang lebih kompleks.
2. Perancangan dapat menggunakan
perangkat lunak yang menyediakan
fitur animasi seperti macromedia
flash agar tampilan grafik dan
animasinya lebih bagus dan menarik
DAFTAR PUSTAKA
Ario Suryokusumo, Microsoft Visual Basic
6.0, PT Elekmedia Komputindo, 2001
Djoko Promono, Mudah Menguasai Visual
Basic 6.0, PT.Elekmedia Komputindo,
2002
Edwin J. Purcell, Dale Varberg, Kalkulus dan
Geometri Analitis, Jilid 1, Edisi Keima,
PT. gelora Aksara Pratama, 1987
James Stewart, Kalkulus, jilid 1, edisi
Keempat, PT. gelora aksara Pratama,
1998
Hadi, Rahadian, Pemrograman Microsoft
Visual
Basic,
PT.
Elekmedia
Komputindo, Jakarta, 2001
Ismail Basari, Matematika Universitas,
Armico, Bandung 1980
Koko Martono, Kalkulus, PT. Gelora Aksara
Pratama, 1999
Murray R. Sipegel, Kasir Iskandar, seri Buku
Schau, PT. Gelora Aksara Pratama,
1984
Rinaldi MUnir, Buku Teks lmu KOmputer,
Matematika
Diskrit,
Penerbit
Informatika Bandung, 2001
Seymour Lipscutz, Marc Lars Lipson,
Matematika Diskrit, Tim Editor
Salemba Teknika, Jilid 1.
V. KESIMPULAN DAN SARAN
5.1 Kesimpulan
Dari
pembahasan-pembahasan
sebelumnya
dan
percobaan-percobaan
yangtelah dilakukan, maka dapat diambil
beberapa kesimpulan yaitu:
1. Program dapat digunakan untuk
mempermudah penggambaran grafik
secara manual.
2. Program dapat digunakan sebagai
media alternatif untuk membantu
mengerjakan
penerapan
fungsi
integral tetu untuk menghitung isi
benda putar.
3. Semakin besar nilai variabel, batas
atas dan batas bawah yang
dimasukkan,
perhitungan
skala
gambar da nisi benda putar akan
semakin besar.
43