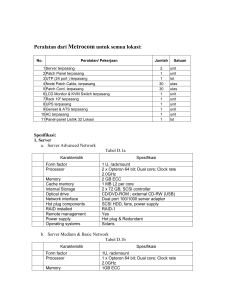
Makalah Struktur data
advertisement

TREE
BINARY TREE TRAVERSAL, BALANCING BINARY
SEARCH TREE, BOUND BALANDCE TREE
DISUSUN OLEH
: KELOMPOK 4
1.
2.
3.
4.
5.
6.
DOSEN PEMBIMBING
Septi Rizky A R
Seri Gustina
Silvia Dewi Sabrina
Sulaiman
Tatu Buhaya
Vidia Rahmadhani
(13540141)
(13540142)
()
(13540150)
(13540153)
(13540156)
:
JURUSAN SISTEM INFORMASI
FAKULTAS DAKWAH DAN KOMUNIKASI
UIN RADEN FATAH PALEMBANG
TAHUN 2014
KATA PENGANTAR
Puji Syukur kami panjatkan kehadirat Allah SWT karena berkat limpahan rahmat
dariNya kami selaku Kelompok 4 dapat menyelesaikan makalah ini tepat pada waktunya,
walaupun dalam keadaan yang sangat sederhana. Makalah ini berisikan tidak lanjut dari
materi pembelajaran kita Pada Tree dan Tree Biner. Dengan segala keterbatasan yang kami
miliki kami sajikan makalah ini dalam bentuk yang sangat sederhana maka dari itu kami
selaku panyaji meminta maaf yang sebesar-besarnya jika makalah ini masih begitu banyak
kekurangan, baik itu yang kami sengaja ataupun tidak sengaja karena ini semua masih
dalam proses pembelajaran kami yang tentunya tak lepas dari kodrad kami sebagai manusia
biasa yang tak akan pernah luput dari kesalahan dan tentunya makalah ini masih sangat jauh
dari sempurna. Semoga makalah ini dapat bermanfaat untuk memberikan wawasan kepada
kalian semua bagi para pembaca. Untuk itu kepada dosen kami untuk meminta masukan,
kritikan atau saran yang membangun untuk melengkapi kekurangan yang ada di makalah ini.
Atas perhatiannya kami selaku Kelompok 4 mengucapkan terima kasih.
Palembang , Desember 2014
BAB I
PENDAHULUAN
1.1. Latar belakang
Pohon(tree) adalah salah satu jenis graf yang tidak memiliki lintasan atau sirkuit.
Pohon biasanya memiliki hanya satu simpul orangtua dan simpul anak yang bisa nol atau
lebih dari nol. Pada pohon juga terdapat yang disebut pohon berakar yaitu pohon yang
satu buah simpulnya dijadikan sebuah akar lalu anak dari akar tersebut akan memiliki
simpul anak dan simpul anak tersebut akan terus memiliki anak sehingga akan ada simpul
yang tidak memiliki anak yang disebut simpul daun.
A
B
D
D
E
Gambar 1-1. Gambar Pohon Berakar
Dalam gambar pohon berakar di atas(Gambar 1-1). Dapat dilihat beberapa terminologi:
A adalah akar dari pohon tersebut
B dan C adalah anak dari A
B adalah orangtua dari D dan E
C,D dan E adalah daun dari pohon
A,B,C,D,E adalah simpul dari pohon
D dan E adalah cucu dari A
Tinggi pohon tersebut adalah 2(akar tidak dihitung)
Dan berlaku hubungan lainya seperti pohon keluarga
Dalam pohon terdapat berbagai jenis pohon, antara lain adalah pohon biner, dan pohon
pencarian biner.
1.2.Tujuan
a. Memahami tentang Tree
b. Mengetahui istilah-istilah dalam Tree
c. Memahami pengertian dari Binary Tree
d. Mengetahui jenis-jenis Binary Tree
e. Memahami transversal
f. Memahami tentang Balancing binary search tree serta contohnya
g. Memahami tentang Bound Balance serta contohnya
BAB II
PEMBAHASAN
2.1. Pengertian Tree
Tree merupakan salah satu bentuk struktur data tidak linear yang menggambarkan
hubungan yang bersifat hierarkis (hubungan one to many) antara elemen-elemen. Tree bias
didefinisikan sebagai kumpulan simpul/node dengan elemen khusus yang disebut Root.
Notde lainnya terbagi menjadi himpunan-himpunan yang saling tak berhubungan satu sama
lain (disebut Subtree).
Deklarasi Pohon
Jika kita memperhatikan setiap simpul dalam pohon biner, kita bisa menyusun
struktur data yang tepat dari simpul-simpul tersebut. Kita dapat melihat bahwa dalam
setiap simpul selalu berisi dua buah pointer untuk menunjuk ke cabang kiri dan cabang
kanan, dan informasi yang akan disimpan dalamsimpul tersebut. Dengan memperhatikan
hal ini, simpul dalam pohon biner disajikan sebagai berikut:
KIRI
INFO
KANAN
Gambar 7.1
Sesuai dengan gambar 7.1, maka deklarasi list yang sesuai adalah:
typedef char TypeInfo;
typedef struct Simpul *Tree;
struct Simpul {
TypeInfo Info;
tree Kiri, /* cabang kiri */
Kanan; /* cabang kanan */
};
Untuk lebih jelasnya, di bawah akan diuraikan istilah-istilah umum dalam tree.
a. Predecessor : Node yang berada di atas node tertentu
b. Successor
: Node yang berada dibawah node tertentu
c. Ancestor : Seluruh node yang terletak sebelum node tertentu dan terletak pada jalur
yang sama
d. Descendant Seluruh node yang terletak sebelum node tertentu dan terletak pada jalur
yang sama
e. Parent Predecessor satu level di atas suatu node
f. Child Successor satu level di bawah suatu node
g. Sibling Node-node yang memiliki parent yang sama dengan suatu node
h. Subtree Bagian dari tree yang berupa suatu node beserta descendantnya dan memiliki
semua karakteristik dari tree tersebut.
i. Size Banyaknya node dalam suatu tree
j. Height Banyaknya tingkatan / level dalam suatu tree
k. Root Satu-satunya node khusus dalam tree yang tak punya predecessor
l. Leaf Node-node dalam tree yang tak memiliki successor
m. Degree Banyaknya child yang dimiliki suatu node
2.2. Jenis-Jenis Tree
1. Binary Tree
Binary Tree adalah tree dengan syarat bahwa tiap node hanya boleh memiliki
maksimal dua subtree dan kedua subtree tersebut harus terpisah. Sesuai dengan definisi
tersebut tiap node dalam binary tree hanya boleh memiliki paling banyak dua child.
Jenis- Jenis Binary Tree :
a. Full Binary Tree
Jenis binary tree ini tiap nodenya (kecuali leaf) memiliki dua child dan tiap
subtree harus mempunyai panjang path yang sama.
b. Complete Binary Tree
Jenis ini mirip dengan Full Binary Tree, namun tiap subtree boleh memiliki
panjang path yang berbeda dan setiap node kecuali leaf hanya boleh memiliki 2 child.
c. Skewed Binary Tree
Skewed Binary Tree adalah Binary Tree yang semua nodenya (kecuali leaf)
hanya memiliki satu child.
1.1.Implementasi Binary Tree
Binary tree dapat diimplementasikan dalam C++ dengan menggunakan double
linkedlist.
1.2.Operasi-Operasi pada Binary Tree
Create
: Membentuk binary tree baru yang masih kosong
Clear
: Mengosongkan binary tree yang sudah ada
Empty
: Function untuk memeriksa apakah binary tree masih kosong
Insert
: Memasukkan sebuah node ke dalam tree. Ada tiga pilihan insert :
sebagai root, left child, atau right child. Khusus insert sebagai root, tree
harus dalam keadaan kosong
Find
: Mencari root, parent, left child, atau right child dari suatu node. (tree
tidak boleh kosong).
Update
: Mengubah isi dari node yang ditunjuk oleh pointer curret (Tree tidak
boleh kosong)
Retrieve
: Mengetahui isi dari node yang ditunjuk oleh pointer current (Tree
tidak boleh kosong)
Delete Sub
: Menghapus sebuah subtree (node beserta seluruh descendantnya)
yang ditunjuk current. Tree tidak boleh kosong. Setelah itu, pointer
current dakan berpindah ke parent dari node yang dihapus.
Characteristic : Mengetahui karakteristik dari suatu tree, yakni: size, height, serta
average length. Tree tidak boleh kosong.
Traverse
: Mengunjungi seluruh node-node pada tree, masing-masing sekali.
Hasilnya adalah urutan informasi secara linear yang tersimpan dalam
tree. Ada tiga cara traverse,yaitu PreOrder, InOrder, dan PostOrder.
Langkah-langkah Tranverse :
PreOrder : cetak isi node yang dikunjungi, kunjungi Left Child, kunjungi Right Child
InOrder : kunjungi Left Child, cetak isi node yang dikunjungi, kunjungi Right Child
PostOrder : kunjungi Left Child, kunjungi Right Child cetak isi node yang dikunjungi.
2. Binary Search Tree
Binary Tree ini memiliki sifat dimana semua left child harus lebih kecil dari
pada right child dan parentnya. Semua right child juga harus lebih besar dari left child
serta parentnya.
Binary search tree dibuat untuk mengatasi kelemahan pada binary tree biasa,
yaitu kesulitan dalam searching / pendarian node tertentu dalam binary tree. Pada
dasarnya operasi dalam Binary Search Tree sama dengan Binary Tree biasa, kecuali
pada operasi insert, update, dan delete.
Insert
Pada Binary Search Tree insert dilakukan setelah lokasi yang tepat ditemukan
(lokasi tidak ditentukan oleh user sendiri ).
Update
Update ini seperti yang ada pada Binary Tree biasa, namun di sini update akan
berpengaruh pada posisi node tersebut selanjutnya. Bila update mengakibatkan tree
tersebut bukan Binary Search Tree lagi, harus dilakukan perubahan pada tree dengan
melakukan rotasi supaya tetap menjadi Binary Search Tree.
Delete
Seperti halnya update, delete dalam Binary Search Tree juga turut mempengaruhi
struktur dari tree tersebut.
AVL Tree
AVL Tree adalah Binary Search Tree yang memiliki perbedaan tinggi/ level
maksimal 1 antara subtree kiri dan subtree kanan. AVL Tree muncul untuk
menyeimbangkan Binary Search Tree. Dengan AVL Tree, waktu pencarian dan bentuk
tree dapat dipersingkat dan disederhanakan. Selain AVL Tree, terdapat pula Height
Balanced n Tree, yakni Binary Search Tree yang memiliki perbedaan level antara
subtree kiri dan subtree kanan maksimal adalah n sehingga dengan kata lain AVL Tree
adalah Height Balanced 1 Tree. Untuk memudahkan dalam menyeimbangkan tree,
digunakan simbol-simbol Bantu :
-- (tanda minus) : digunakan apabila Subtree kiri lebih panjang dari Subtree kanan.
+ (tanda plus) : digunakan apabila Subtree kanan lebih panjang dari Subtree kiri.
0 (nol)
: digunakan apabila Subtree kiri dan Subtree kanan mempunyai height
yang sama.
Daftar Istilah-Istilah
Algoritma : Langkah-langkah menyelesaikan suatu masalah yang disusun
secara logis dan berurutan
Animasi : Gambar yang tampak bergerak, terdiri dari banyak gambar-gambar
tunggal (disebut frame) yang ditampilkan satu per satu secara bergantian dengan
cepat sehingga objek dalam gambar tampak seolah-olah bergerak.
Array : Struktur data yang memiliki banyak elemen di dalamnya, dengan
masing-masing elemen memiliki tipe data yang sama.
Clear : Menghapus secara keseluruhan, biasanya digunakan sebagai nama
fungsi/metode yang bertujuan untuk mengosongkan list atau menghapus
keseluruhan elemen.
Console : Istilah dalam komputer yang menunjuk pada antarmuka antara
pemakai dengan komputer yang berbasiskan teks. Cara kerja konsol sangat
sederhana yaitu menggunakan standar input untuk membaca input dari keyboard
dan standar output untuk menampilkan teks ke layer monitor.
Data : Informasi yang disimpan komputer, dapat berbentuk teks, gambar, suara,
video, dan sebagainya.
Delete : Menghapus sebuah elemen, biasanya digunakan sebagai nama
fungsi/metode yang bertujuan untuk menghapus sebuah elemen dalam suatu
list/tree
Deret geometric : Deretan bilangan yang setiap bilangan merupakan hasil kali
bilangan sebelumnya dengan suatu konstanta.
Destruktor : Metode khusus dalam sebuah kelas untuk menghapus objek hasil
instansiasi kelas tersebut
Dimensi : Jumlah indek yang diperlukan untuk menyatakan sebuah elemen
dalam array
Elemen : Sebuah data tunggal yang paling kecil dari sebuah array atau list. Data
tunggal disini tidak perlu data sederhana, melainkan bisa berupa kumpulan data
atau list yang lain.
Empty : Keadaan di mana list ada dalam keadaan kosong
Fibonacci : Barisan bilangan yang setiap bilangan merupakan jumlah dari dua
bilangan sebelumnya.
Field : Data yang dimiliki oleh sebuah objek
FIFO : First In First Out sifat suatu kumpulan data. jika sebuah elemen A
dimasukkan lebih dulu dari B maka A harus dikeluarkan dulu dari B
FPB : Faktor Persekutuan terbesar, faktor yang paling besar jika sejumlah
bilangan memiliki beberapa faktor yang sama.
Full : Keadaan di mana list penuh, tidak boleh menerima data lagi
Fungsi : Suatu modul atau bagian program yang mengerjakan suatu program
tertentu.
Himpunan : Kumpulan dari objek-objek, misalnya sebuah himpunan dari buahbuahan dapat terdiri dari pisang, mangga, jambu dll.
Indeks : Bilangan yang digunakan untuk menyatakan posisi suatu elemen dalam
array atau list.
Input : Data masukkan, dalam fungsi berarti parameter yang dimasukkan,
sedangkan dalam program secara keseluruhan berarti data yang dimasukkan
pemakai, bias melalui parameter program, file maupun lewat keyboard
Insert : Memasukkan sebuah elemen baru ke dalam list. Biasanya insert
dilakukan baik di tengah-tengah list, awal, maupun di akhir list.
Iterasi : Perulangan dengan struktur perulangan, while, do while, maupun for.
Kelas : Suatu struktur yang digunakan sebagai template bagi objek-objek yang
sama sifatnya.
Kompilasi : Proses menerjemahkan bahasa sumber (source code) ke dalam
bahasa lain, biasanya bahasa mesin, untuk dapat dijalankan langsung oleh
computer melalui system operasi.
Kompiler : Program yang mengerjakan kompilasi.
Konstruktor : Metode khusus yang dimiliki suatu kelas untuk membentuk
suatu objek baru berdasarkan kelas tersebut
Library : Kumpulan fungsi, makro, template, dan kelas yang disediakan
bersama compiler C++.
LIFO : Last In Fisrt Out, sifat kumpulan data, kebalikan dari FIFO
Linked List : List yang didesain dengan cara mendefinisikan sebuah elemen
yang memiliki hubungan atau link dengan elemen lain yang dihubungkan
dengan elemen yang lain lagi.
Matriks : Dalam matematika berarti kumpulan bilangan yang disusun dalam
bentuk kolom dan baris.
Metode : Fungsi yang dimiliki suatu objek
Objek : Struktur data yang terdiri dari data yang lebih sederhana yang disebut
field yang memiliki operasi sendiri untuk menangani data-data yang
dimilikinya.
Output : Data yang dihasilkan oleh program
Pointer : Type data khusus yang pada umumnya berukuran 32 bit yang
berfungsi untuk menampung bilangan tertentu yang menunjuk pada lokasi
memory tertentu
Pop : Mengeluarkan satu elemen dari dalam list dengan cara menyalin data
elemen tersebut, kemudian menghapus elemen tersebut dari list biasanya
digunakan untuk stack.
Prima : Bilangan yang tidak memiliki faktor selain 1 dan bilangan itu sendiri.
Push : Memasukkan sebuah elemen baru ke dalam list.
Queue : Struktur list dengan sifat FIFO, cara kerjanya seperti antrian manusia.
Record : Struktur data yang terdiri dari satu atau lebih elemen yang tipe data
bias berbeda.
Rekursi : Jenis perulangan yang tidak menggunakan struktur perulangan, tetapi
dengan memanggil fungsi yang bersangkutan.
Sort : Menyusun elemen-elemen suatu list secara berurutan.
Source Code : Program yang ditulis menggunakan bahasa pemrograman
tertentu. Kode sumber belum dapat dijalankan oleh komputer dan perlu
menjalani proses kompilasi sehingga dapat dijalankan.
Stack : List yang memiliki sifar LIFO. Data yang hendak di keluarkan dari stack
haruslah data yang paling terakhir dari stack.
STL : Standar Templete Library merupakan kumpulan yang disertakan dalam
setiap compiler C++ yang memenuhi standar ANSI C++ yang menyediakan
berbagai struktur data, algoritma dan template yang sering dipakai.
Stream : Aliran merupakan konsep dalam C++ untuk input dan ouput data tanpa
memperdulikan isi data maupun media penampung data tersebut.
Struktur kontrol : Struktur yang digunakan untuk mengontrol jalannya
program.
Teks : Data yang terdiri dari karakter-karakter yang dapat dibaca (huruf
bilangan, tanda baca).
Tree : Suatu struktur data yang setiap elemen terhubung sedemikian rupa
sehingga berbentuk seperti pohon.
Contoh Program:
#include<stdio.h>
typedef struct node{
char data;
node *kiri;
node *kanan;
};
node *akar=NULL;
addNode(node **akar, char isi) {
if((*akar)==NULL){
node *baru;
baru= new node;
baru->data = isi;
baru->kiri = NULL;
baru->kanan = NULL;
(*akar)=baru;
}
}
preOrder(node *akar) {
if(akar !=NULL) {
printf("%c ", akar->data);
preOrder(akar->kiri);
preOrder(akar->kanan);
}
}
inOrder(node *akar) {
if(akar !=NULL) {
inOrder(akar->kiri);
printf("%c ", akar->data);
inOrder(akar->kanan);
}
}
postOrder(node *akar) {
if(akar !=NULL) {
postOrder(akar->kiri);
postOrder(akar->kanan);
printf("%c ", akar->data);
}
}
main(){
char abjad;
printf("\n\n\tPosisi Awal Tree:\n\n");
printf("\t B\n\t / \\\n\t U H\n\t /\n\t A\n\t / \\\n\t Y A\n\n");
addNode(&akar,abjad='B');
addNode(&akar->kiri,abjad='U');
addNode(&akar->kanan,abjad='H');
addNode(&akar->kiri->kiri,abjad='A');
addNode(&akar->kiri->kiri->kiri,abjad='Y');
addNode(&akar->kiri->kiri->kanan,abjad='A');
printf("Tampilan PreOrder : ");
preOrder(akar);
printf("\nTampilan InOrder : ");
inOrder(akar);
printf("\nTampilan PostOrder : ");
postOrder(akar);
}
Hasil output :
2.3. Pengertian Binary Transversal
Traversal
Traversal adalah proses kunjungan dalam pohon, dengan setiap node hanya
dikunjungi tepat satu kali.
Jadi, binary tree traversal adalah proses mengunjungi node tepat satu kali dan tiap
node hanya boleh memiliki maksimal 2 subtree yang disebut sebagai sub pohon kiri
(left subtree) dan sub pohon kanan (right subtree).
Dengan melakukan kunjungan secara lengkap, maka akan didapatkan urutan
informasi secara linier yang tersimpan dalam sebuah binary tree.
Binary tranversal Adalah proses menelusuri suatu Binary Tree sehingga
sedemikian rupa setiap vertex dikunjungi hanya 1 kali.
3 aktivitas dalam Binary tree Transversal :
a. Visit the Root
b. Transverse the left subtree
c. Transverse the right subtree
Algoritma dalam Binary Tree Transversal :
1.
PRE-ORDER TRANSVERSAL
a. visit the root
b. tranverse the left subtree
c. tranverse the right subtree
contoh : { PreOrder }
procedure PreOrder(Tree : NodePtr);
begin
if Tree<>nil then
begin
write(Tree^.value);
PreOrder(Tree^.left);
PreOrder(Tree^.right);
end;
end;
2. IN-ORDER TRANSVERSAL
a. tranverse the left subtree
b. visit the root
c. tranverse the right subtree
contoh :{ InOrder }
procedure InOrder(Tree : NodePtr);
begin
if Tree<>nil then
begin
InOrder(Tree^.left);
write(Tree^.value);
InOrder(Tree^.right);
end;
end;
3. POST-ORDER TRANSVERSAL
a. tranverse the left subtree
b. tranverse the right subtree
c. visit the root
Contoh : { PostOrder }
procedure PostOrder(Tree : NodePtr;
begin
if Tree<>nil then
begin
PostOrder(Tree^.left);
PostOrder(Tree^.right);
write(Tree^.value);
end;
end;
(1)
+
+
*
A
D
C
B
PRE-ORDER : V L R (+ + * A B C D)
(2)
+
+
D
*
C
A
B
IN-ORDER : L V R
A*B+C+D
(3)
+
+
*
A
D
C
B
POST-ORDER : L R V
AB*C+D+
Contoh program PRE-ORDER , IN-ORDER , POST-ORDER
#include<stdio.h>//header file
#include<conio.h>
/* Deklarasi struct */
typedef struct Node{
int data;
//data pada tree
Node *kiri; //penunjuk node anak kiri
Node *kanan; //penunjuk node anak kanan
};
/* Fungsi untuk memasukkan data ke dalam tree */
void tambah(Node **root, int databaru){
if((*root) == NULL){
//jika pohon/subpohon masih kosong
Node *baru;//node "baru" dibentuk…
baru = new Node;//berdasarkan struct "Node"
baru->data = databaru; //data node baru diisi oleh variabel databaru
baru->kiri = NULL;//penunjuk kiri node baru masih kosong
baru->kanan = NULL;//penunjuk kanan node baru masih kosong
(*root) = baru; //node pohon (root) diletakkan pada node baru
(*root)->kiri = NULL;//penunjuk kiri node root masih kosong
(*root)->kanan = NULL; //penunjuk kanan node root masih kosong
printf("Data bertambah!");
}
else if(databaru < (*root)->data)//jika databaru kurang dari data node root…
tambah(&(*root)->kiri, databaru);//tambahkan databaru pada subpohon kiri
else if(databaru > (*root)->data)//jika databaru lebih dari data node root…
tambah(&(*root)->kanan, databaru); //tambahkan databaru pada subpohon kanan
else if(databaru == (*root)->data)//jika databaru sama dengan data node root
printf("Data sudah ada!");//databaru tidak dapat ditambahkan pada tree
}
/* Fungsi untuk menampilkan data secara pre-order
(data ditampilkan dari node induk, node anak kiri, lalu node anak kanan)
*/
void preOrder(Node *root){
if(root != NULL){//jika pohon/subpohon tidak kosong
printf("%d ", root->data);//menampilkan data node yang dikunjungi
preOrder(root->kiri);//mengunjungi node anak kiri
preOrder(root->kanan); //mengunjungi node anak kanan
}
}
/* Fungsi untuk menampilkan data secara in-order
(data ditampilkan dari node anak kiri, node induk, lalu node anak kanan)
*/
void inOrder(Node *root){
if(root != NULL){//jika pohon/subpohon tidak kosong…
inOrder(root->kiri);//mengunjungi node anak kiri
printf("%d ", root->data);//menampilkan data node yang dikunjungi
inOrder(root->kanan);//mengunjungi node anak kanan
}
}
/* Fungsi untuk menampilkan data secara post-order
(data ditampilkan dari node anak kiri, node anak kanan, lalu node induk)
*/
void postOrder(Node *root){
if(root != NULL){//jika pohon/subpohon tidak kosong
postOrder(root->kiri); //mengunjungi node anak kiri
postOrder(root->kanan);//mengunjungi node anak kanan
printf("%d ", root->data); //menampilkan data node yang dikunjungi
}
}
main(){
int pil, c;
Node *pohon, *t;
pohon = NULL;
do{
int data;
printf("MENU\n");
printf("1. Tambah\n");
printf("2. Lihat Pre-Order\n");
printf("3. Lihat In-Order\n");
printf("4. Lihat Post-Order\n");
printf("5. Exit\n");
printf("Pilihan : "); scanf("%d", &pil);
switch(pil){
case 1 :
printf("Data baru : ");
scanf("%d", &data);
tambah(&pohon, data);
break;
case 2 :
if(pohon != NULL)
preOrder(pohon);
else
printf("Masih kosong!");
break;
case 3 :
if(pohon != NULL)
inOrder(pohon);
else
printf("Masih kosong!");
break;
case 4 :
if(pohon != NULL)
postOrder(pohon);
else
printf("Masih kosong!");
break;
}
getch();
printf("\n");
}
while(pil != 5);
}
Maka hasil outputnya
2.4. BALANCING BINARY SEARCH TREE(Self Balancing Binary Tree)
Self Balancing Binary Search Tree adalah pohon pencarian biner yang dapat
menyeimbangkan dirinya sendiri, yaitu meminimalisasikan kedalaman pohon, pada saat
pohon tersebut di tambahkan atau dikurangi simpulnya.
4
3
5
1
2
Gambar 2-1. Pohon Pencarian Biner Tak Seimbang
Pada umumnya dalam Self Balancing Binary Search Tree, bentuk pohon yang
seharusnya seperti gambar 2-1, akan secara otomatis diubah menjadi seperti gambar 12. Algoritma penyeimbangan pohon akan berjalan saat dimasukan simpul baru atau saat
sebuah simpul dalam pohon dihapus.
Pada umumnya Self Balancing Binary Search Tree mempunyai tinggi maksimal
sebesar [2log n] dengan n adalah jumlah simpul, hal ini disebabkan oleh pohon pasti
mempunyai ketinggian minimal dan baru akan menambah tinggi saat pohon sudah
mempunyai daun maksimal di suatu ketinggian, hal ini juga menyebabkan sebagian
besar algoritma untuk mengerjakan pohon ini mempunyai kompleksitas sebesar O(log
n).
Self Balancing Binary Search Tree sangat berguna untuk mempercepat kinerja
sebuah pohon pencarian biner, selain itu pohon ini juga mempunyai beberapa aplikasi
untuk mempermudah kinerja suatu algoritma seperti antrian dengan prioritas dan tabel
data.
Self Balancing Binary Search Tree mempunyai beberapa contoh pohon yaitu:
1. AA tree
2. AVL tree
3. Red-black tree
4. Scapegoat tree
5. Treap
2.4.1. JENIS-JENIS SELF BALANCING BINARY SEARCH TREE
A. Red-black Tree
Red-black Tree adalah salah satu jenis Self Balancing Binary Search Tree
yang diciptakan oleh Rudolf Bayer di tahun 1972 dan bernama Symmetric binary
B-tree, lalu pada tahun 1978 diperbaharui menjadi Red-black Tree oleh Leonidas J.
Guibas dan Robert Sedgewick.
Dalam Red-black Tree ini pohon, simpul ditambahkan dan dihapus dengan
algoritma khusus sehingga pohon tidak perlu menyeimbangkan dirinya.
Selain kriteria pohon pencarian biner biasa, ada beberapa kriteria tambahan berlaku
untuk Red-Black Tree:
1. Simpul bewarna merah atau hitam.
2. Akar berwarna hitam. (Aturan ini dapat dihilangkan karena akar dapat diubah
ke merah dan tidak mempengaruhi.)
3. Anak dari tiap simpul merah adalah hita
4. Setiap jalur dari akar sampai simpul sampai daun keturunannya mempunyai
jumlah simpul hitam yang sama.
11
14
44
4
2
1
7
5
15
8
Gambar 3-1. Contoh Red-black Tree
Pada pohon ini algoritma menambahkan dan mengurangkan bergantung pada
kasus dan beberapa diantaranya menggunakan rotasi pohon seperti pada gambar 3-2.
Gambar 3-2. Rotasi sebuah pohon biner
Sumber: http://www.cs.auckland.ac.nz/~jmor159/PLDS210/red_bl ack.html
Pohon ini menambahkan dan mengurangkan dengan cara melihat dimana
simpul baru akan ditambahkan dan tergantung dimana simpul tersebut ditambahkan
akan ada algoritma tersendiri.
Contoh beberapa kasus :
1) Simpul baru menjadi akar.
2) Simpul orangtua bewarna hitam.
3) Simpul orangtua bewarna merah.
B. AVL Tree
AVL Tree adalah salah satu jenis Self Balancing Binary Search Tree yang
ditemukan oleh G.M. Adelson-Velskii and E.M. Landis pada tahun 1962. Di pohon
ini terdapat balance factor yaitu nilai ketinggian anak pohon dikiri kurang
ketinggian anak pohon kanan. Dan pohon dianggap seimbang bila balance factor
bernilai -1,0, atau 1.
Dalam AVL Tree penambahan dan pengurangan dilakukan sama seperti
pohon pencarian biner biasa, hanya saja setelah penambahan atau pengurangan
tersebut akan ditambahkan prosedur rotasi pohon untuk menyeimbangkan.
Dalam penambahan atau pengurangan, pertama akan di cek balance factor
apakah -2 atau +2. Lalu setelah itu akan dicek kembali balance factor dari kedua
sub-pohon dari pohon utama. Lalu akan dilakukan rotasi sesuai kebutuhan.
Gambar 3-3. Diagram algoritma AVL Tree
Sumber: http://en.wikipedia.org/wiki/AVL_tree
Dapat dilihat pada gambar 3-3 pohon berputar sesuai dengan kedaan pohon
tersebut dan pada akhirnya pohon menjadi seimbang.
C. AA Tree
AA Tree adalah salah satu jenis Self Balancing Binary Search Tree yang
ditemukan oleh Arne Andersson. Pohon ini merupakan varian dari Red-black Tree.
Dalam pohon ini terdapat beberapa syarat seperti Red-Black Tree. Dalam
persyaratan sebagai pengganti warna digunakan bilangan level simpul.
Beberapa persyaratannya adalah:
1. Level dari daun adalah 1
2. Level dari simpul kiri harus lebih kecil dari simpul orangtua
3. Level dari simpul kanan bisa lebih kecil atau sama dengan orangtua.
4. Level dari cucu kanan selalu lebih besar dari level kakeknya
5. Simpul yang level-nya lebih besar dari satu harus mempunyai dua anak
Pada saat menambahkan atau mengurangkan pada pohon ini berlaku pengurangan
dan penambahan seperti pohon pencarian biner biasa. Hanya
saja untuk
menyeimbangakn akan ditambahkan dua prosedur yaitu Skew dan Split(Gambar 3-4).
Dan karena dua pohon tersebut aka nada keadaan dimana ada simpul horizontal untuk
sementara.
Gambar 3-4. (a) Skema Prosedur Skew. (b) Skema Prosedur Split
Sumber: http://en.wikipedia.org/wiki/AA_tree
Dalam penambahan dan pengurangan akan diadakan pengubahan level agar
pohon sesuai dengan ketentuan yang berlaku.
D. Scapegoat Tree
Scapegoat Tree adalah salah satu jenis Self Balancing Binary Search Tree
yang diciptakan oleh Igal Galperin, Jacob Tepec and Ronald L. Rivest.
Pohon pencarian biner akan dikatan seimbang beratnya jika jumlah simpul di
sub-pohon kanan sama dengan jumlah simpul di pohon kiri. Dan dari ketentuan
tersebut didapat rumus
size(left) <= α*size(node)
size(right) <= α*size(node)
Dimana size adalah jumlah node dan bila memenuhi rumus tersebut disebut
α-weight-balanced.
Selain itu sebuah pohon yang seimbang beratnya juga harus seimbang
tingginya dan dari sana didapt rumus.
height(tree) <= log1/α(NodeCount)
dan bila memenuhi rumus tersebut disebut α-height-balanced.
Dan dalam Scapegoat Tree akan selalu dipastikan pohon akan memenuhi
α-height-balanced walaupun belum dipastikan memenuhi α-weight-balanced.
α disini dapat diubah-ubah sesuai ketentuan, dan pengubahan α
berpengaruh pada kinerja pohon (apakah pohon cepat saat menambahkan atau
menghapus).
Penambahan pada pohon ini dilakukan dengan cara seperti penambahan
pada pohon pencarian biner biasa tetapi dengan penambahan scapegoat dan
perhitungan jumlah dan ketinggian simpul yang akan digunakan untuk
penyeimbangan. Dalam penghapusannya juga akan menggunakan jumlah simpul
untuk memastikan apakah penyeimbangan perlu dilakukan atau tidak.
E. Splay Tree
Scapegoat Tree adalah salah satu jenis Binary Search Tree yang dapat
menjadi Self Balancing Binary Search Tree. diciptakan Daniel Dominic Sleator and
Robert Endre Tarjan tahun 1985. Pohon ini mempunyai ketentuan tambahan yaitu
elemen yang baru saja diakses akan mudah dan cepat diakses lagi.
Semua kejadian yang diatur dalam Splay Tree disebut Splaying. Dalam
Splaying, sebuah simpul akan diatur seperti biasa lalu dilanjutkan dengan rotasi
pohon agar pohon tetap seimbang dan simpul yang mengandung elemen yang
mudah diakses tersebut dipindah menjadi akar.
Setiap kali elemen x diakses, Splay akan membawanya ke akar sehingga
terdapat beberapa dan tahap-tahap tersebut tergantung beberapa factor yaitu:
Apakah x adalah simpul kanan atau kiri dari orangtuanya(simpul p)
Apakah p akar atau bukan
Apakah p adalah simpul kanan atau kiri dari
listing 1
def _put (self, key, val, CurrentNode):
jika kunci <currentNode.key:
jika currentNode.hasLeftChild ():
self._put (key, val, currentNode.leftChild)
lain:
currentNode.leftChild = TreeNode (key, val, orang tua = CurrentNode)
self.updateBalance (currentNode.leftChild)
lain:
jika currentNode.hasRightChild ():
self._put (key, val, currentNode.rightChild)
lain:
currentNode.rightChild = TreeNode (key, val, orang tua = CurrentNode)
self.updateBalance (currentNode.rightChild)
def updateBalance (self, node):
jika node.balanceFactor> 1 atau node.balanceFactor <-1:
self.rebalance (node)
kembali
jika node.parent = Tidak:
jika node.isLeftChild ():
node.parent.balanceFactor = 1
Elif node.isRightChild ():
node.parent.balanceFactor - = 1
jika node.parent.balanceFactor = 0:
self.updateBalance (node.parent)
Metode updateBalance baru di mana sebagian besar pekerjaan dilakukan. Ini
menerapkan prosedur rekursif kita hanya dijelaskan. Metode updateBalance cek
pertama untuk melihat apakah node saat ini tidak seimbang cukup membutuhkan
rebalancing (baris 16). Jika itu terjadi maka rebalancing dilakukan dan tidak ada
update lebih lanjut untuk orang tua diperlukan. Jika node saat ini tidak memerlukan
rebalancing maka faktor keseimbangan induk disesuaikan. Jika faktor keseimbangan
induk non-nol maka algoritma terus bekerja dengan cara naik pohon ke arah akar
dengan rekursif memanggil updateBalance pada orang tua.
2.5. BOUND BALANCE
BAB III
PENUTUP
3.1. Kesimpulan
Tree merupakan salah satu bentuk struktur data tidak linear yang menggambarkan
hubungan yang bersifat hirarkis (hubungan one to many) antara elemen-elemen. Tree
bisa didefinisikan sebagai kumpulan simpul/node dengan satu elemen khusus yang
disebut Root dan node lainnya
Istilah-istilah pada Tree
1). Predecessor
2). Successor
3). Ancestor
4). Descendant
5). Father
6). Son
7). Sibling
8). Subtree
9). Size
10). Height
11). Root
12). Leaf
13).Degree
Binary Tree adalah tree dengan syarat bahwa tiap node hanya boleh memiliki
maksimal dua sub tree dan kedua subtree tersebut harus terpisah.
Jenis-jenis Binary Tree :
a) Full Binary Tree
b) Complete Binary Tree
c) Skewed Binary Tree
Operasi-operasipada Binary Tree :
Create
Clear
Empty
Insert
Find
Update
Retrieve
Delete Sub
Characteristic
Traverse
Traversal
Traversal adalah proses kunjungan dalam pohon, dengan setiap node hanya
dikunjungi tepat satu kali.
Jadi, binary tree traversal adalah proses mengunjungi node tepat satu kali dan
tiap node hanya boleh memiliki maksimal 2 subtree yang disebut sebagai sub pohon
kiri (left subtree) dan sub pohon kanan (right subtree).
Algoritma dalam Binary Tree Transversal :
1.
Pre-order transversal
2.
In-order transversal
3.
Post-order transversal
Balancing Binary Search Tree
Self Balancing Binary Search Tree adalah pohon pencarian biner yang dapat
menyeimbangkan dirinya sendiri, yaitu meminimalisasikan kedalaman pohon, pada saat
pohon tersebut di tambahkan atau dikurangi simpulnya.
DAFTAR PUSTAKA
1. Desphande P.S., O.G. Kakde (2004). C dan Data Structures. Charles RiverMedia, Inc.
Massachusetts
2. Heriyanto, Imam, Budi Raharjo (2003). Pemrograman Borland C++ Builder. Informatika
Bandung.
3. Solichin, Achmad (2003). Pemrograman Bahasa C dengan Turbo C. IlmuKomputer.Com.
4. Lidya, Leoni, rinaldi Munir (2002). Algoritama dan Pemrograman dalam Bahas Pascal
dan C. Informatika Bandung
5. http://en.wikipedia.org/wiki/Tree_%28data_structure%29
Kamis, 28 November 2014
6. https://agungsetiady.wordpress.com/2012/05/27/binary-tree-traversal
Kamis, 28 November 2014
7. http://en.wikipedia.org/wiki/Binary_search_tree
Senin,1 Desember 2014
8. http://en.wikipedia.org/wiki/AVL_tree
Senin,1 Desember 2010
9. http://en.wikipedia.org/wiki/AA_tree
Senin, 1 Desember 2010
10. http://en.wikipedia.org/wiki/Self-balancing_binary_search_tree
Selasa, 2 Desember 2014
11. http://www.cs.auckland.ac.nz/~jmor159/PLDS210/red_bl ack.html
Selasa, 2 Desember 2014