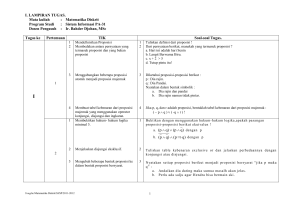
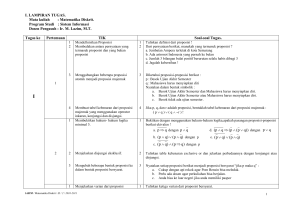
Matematika Disktri II

Matematika Diskrit II
Imam Suharjo
FTI Mercu Buana Yogyakarta
Revisi 2015
Perkenalan Singkat
• Imam Suharjo, S.T., M.Eng
• SMS
: 085 743 723 131
• WA / SMS
: 081 392 979 131
Untuk kontak, silahkan gunakan SMS/WA/Email
•
•
•
•
Email : [email protected]
Email/FB : [email protected]
Web Dosen : imam.mercubuana-yogya.ac.id
Web Personal : imam.web.id
Intro dan Buku
Pengarang : Rinaldi Munir
Penerbit : Informatika
Bandung
Mata Kuliah semeter 2
dengan 2 SKS.
Lanjutan dari Matematika
Diskrit 1.
1. Kombinatorial & Peluang Diskrit
“Hidup adalah penjumlahan semua pilihan yang ada”
(Albert Camus)
a)Percobaan
b)Permutasi
c)Kombinasi
d)Pigeon Hole
e)Peluang
Pokok Materi
Matematika Disktrit 2 :
1.Kombinatorial dan Peluang Disktrit
2.Aljabar Boolean
3.Graf
4.Pohon (tree)
5.Kompleksitas Algoritma
1. Kombinatorial & Peluang Diskrit
• Kombinatorial adalah cabang Matematika yang
mempelajari pengaturan objek-objek.
• Solusi yang diperoleh dengan kombinatorial adalah
jumlah cara pengaturan objek-objek tertentu di dalam
himpunannya dengan Kaidah perkalian dan kaidah
penjumlahan.
• Contoh : Misalkan Plat Nomor Kendaraan Jogja (AB)
terdiri dari 4 digit angka dan 2 huruf Abjad. Berapa
banyak susunan yang terbentuk?
Gambar Plat : id.wikipedia.org/wiki/Tanda_nomor_kendaraan_bermotor
Percobaan
Contoh Percobaan dan hasilnya :
– Melempar mata dadu : 1,2,3,4,5 atau 6
– Melempar koin : Gambar atau angka
– Memilih ketua BEM FIKOM Universitas
dari sejumlah mahasiswa :
– Menyusun susunan 5 huruf yang tidak
boleh berulang :
• Ada Kaidah dan teknik untuk Menghitung?
Permutasi
• Permutasi = jumlah urutan berbeda dari
pengaturan objek-obyek.
http://slideplayer.info/slide/3188481/
Kombinasi
• Contoh : Ada berapa cara memasukan 2 buah kelereng
kedalam 3 kaleng. Masing-masing kaleng hanya boleh
diisi 1 kelereng saja?
http://slideplayer.info/slide/2615359/
2. Aljabar Boolean
a)
b)
c)
d)
e)
Ekspresi Aljabar Boolean
Prinsip Dualitas
Bentuk Kanonik
Aplikasi Aljabar Boolean
Penyederhanaan
Image : http://didik.blog.undip.ac.id
Operasi Logika
OR
AND
XOR
NOR
NAN
NOT
3. Graf
•
•
•
•
Sejarah
Jenis Graf
Representasi Graf
Lintasan
Jembatan Königsberg?
• Pada abad ke-18, di Prussia, terdapat kota bernama
Königsberg, sekarang bernama Kaliningrad, Russia.
Beberapa area kota dipisahkan sungai Pregel sehingga
untuk mencapai area kota yang lainnya penduduk harus
berjalan melalui jembatan yang jumlahnya ada tujuh.
• Bertahun-tahun kemudian, timbul sebuah pertanyaan
pada penduduk Königsberg :
• “Apakah bisa melalui semua jembatan hanya dengan
satu kali jalan?”
• Seorang matematikawan asal Swiss, Leonhard Euler,
berhasil
memecahkan
teka-teki
ini
dengan
menggunakan teori graf.
Jembatan Königsberg?
<-- Königsberg (1951)
Old Königsberg amid
Modern Kaliningrad
Persoalan Tukang Pos Cina?
• Permasalahan : Bagaimana mangatur
ruter perjalanan pak Pos yang efisien?
4. Pohon (Tree)
•
•
•
•
•
Definisi
Sifat Pohon
Pohon berakar
Pohon ekspresi
Pohon keputusan
People trees, by Pooktre
https://en.wikipedia.org/wiki/Tree
Aplikasi Tree
• Spanning tree Protocol
http://www.cisco.com/c/dam/en/us/support/docs/lan-switching/spanning-treeprotocol/10556-16f.gif
5. Kompleksitas Algoritma
• Pengantar : Algoritma tidak hanya benar,
tapi juga perlu efisien (mangkus).
• Pentingnya Algoritma yang Efisien
Daftar Pusataka
1. Kombinatorial, https://prezi.com/wrl53trr1f3c/kombinatorial-danpeluang-diskrit
2. Aljabar Boolean : http://didik.blog.undip.ac.id/2014/03/18/aljabarboolean-dan-sintesis-rangkaian-logika/
3. Operasi Logika : https://learn.sparkfun.com/tutorials/digitallogic/combinational-logic
4. http://www3.nd.edu/~dgalvin1/40210/40210_F12/CGT_early.pdf
5. Jembatan Konigsberg,
http://obrolanmatematika.blogspot.co.id/2011/12/tujuh-jembatankonigsberg.html
6. https://en.wikipedia.org/wiki/Kaliningrad
7. https://en.wikipedia.org/wiki/K%C3%B6nigsberg