FASOR DAN ELEMEN-ELEMEN DASAR RANGKAIAN LISTRIK

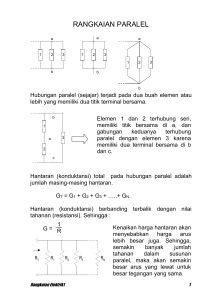
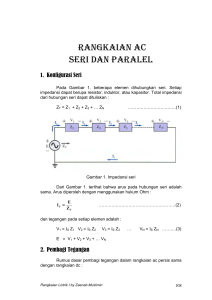
RANGKAIAN PARALEL
1. Pendahuluan
Dua elemen, cabang atau rangkaian terhubung paralel jika
keduanya memiliki dua titik yang sama.
Misalnya seperti pada Gambar 1, elemen 1 dan 2 mempunyai
terminal a dan b yang sama sehingga dapat dikatakan bahwa keduanya
terhubung paralel. Pada Gambar 2 semua elemen terhubung paralel
karena memenuhi kriteria yang telah disebutkan di atas.
Gambar 1. Elemen yang terhubung paralel
Gambar 2. Tiga cara yang berbeda elemen terhubung paralel
Rangkaian listrik I by Zaenab Muslimin
46
Pada Gambar 3, elemen 1 dan 2 terhubung paralel karena
keduanya mempunyai terminal a dan b sama, kombinasi paralel dari 1 dan
2 kemudian seri dengan elemen 3 karena mempunyai titik terminal yang
sama yaitu titik b.
Gambar 3. Rangkaian terhubung paralel dan seri
2. Konduktansi dan Resistansi Total
Untuk elemen-elemen yang terhubung paralel, total
konduktansi
adalah
penjumlahan
dari
konduktansikonduktansi individu.
Yaitu untuk rangkaian paralel seperti pada Gambar 4, kita dapat
menuliskan persamaan;
GT = G1 + G2 + G3 + ... +GN
……………………………………(1)
Gambar 4. Menentukan konduktansi total
Substitusi nilai resistor untuk rangkaian pada Gambar 4, akan
menghasilkan rangkaian seperti pada gambar 5. Karena G = 1/R maka
total resistansi untuk rangkaian paralel dapat ditentukan sebagai berikut;
Rangkaian listrik I by Zaenab Muslimin
47
1
1
1
1
1



 ... 
RT
R1 R 2 R3
RN
..................................................(2)
Gambar 5. Menentukan resistansi total
Resistansi total dari resistor yang terhubung paralel nilainya selalu lebih
kecil dari nilai resistor yang terkecil. Untuk nilai resistor yang sama
terhubung paralel persamaan menjadi lebih mudah. Untuk N resistor yang
sama terhubung paralel persamaan (2) menjadi
1
1 1 1
1
 1
    ...   N  
RT R R R
R
R
RT 
R
N
...................................................................................(3)
Untuk konduktansi kita dapat tuliskan,
GT = N G ……………………………………………………………(4)
Untuk dua buah resistor terhubung paralel;
1
1
1 R2  R1



R T R1 R2
R1 R2
RT 
R1 R2
R1  R2
dan
……………………………………………………..(5)
Untuk tiga buah resistor terhubung paralel;
RT 
1
1
1
1


R1 R2 R3
..............................................................(6.a)
Rangkaian listrik I by Zaenab Muslimin
48
RT 
R1 R2 R 3
R1 R2  R1 R3  R 2 R 3
..................................................(6.b)
3. Rangkaian Paralel
Rangkaian paralel yang paling sederhana dapat dilihat pada
Gambar 6. Total resistansi adalah RT = R1.R2 /(R1 + R2), dan arus sumber
adalah IS=E/ RT. Karena terminal dari baterei dihubungkan langsung pada
R1 dan R2 maka dapat disimpulkan :
Tegangan pada elemen-elemen yang terhubung paralel
adalah sama.
V1 = V2 = E
I1 
V1
E

R1 R1
dan I2 
V2
E

R2 R2
Gambar 6. Rangkaian paralel
Jika resistansi total dihitung dan kedua sisi dikalikan dengan tegangan
sumber diperoleh;
 1
E 
 RT

 1
1
  E 


 R1 R2



dan
E
E
E


RT
R1 R 2
Substitusi hukum Ohm di atas diperoleh arus sumber :
IS = I1 + I2
Rangkaian listrik I by Zaenab Muslimin
49
Daya yang terdisipasi oleh resistor dan yang dikirim oleh sumber dapat
ditentukan dari :
P1  V1 I 1  I 12 R 1 
V12
R1
V22
P2  V2 I 2  I R 2 
R2
2
2
PS  E I S 
E2
RT
4. Hukum Kirchhoff tentang Arus
Hukum Kirchhoff untuk arus yang masuk pada suatu simpul dapat
dirumuskan sebagai berikut :
Jumlah arus yang masuk ke satu simpul sama dengan
jumlah arus yang keluar dari simpul tersebut atau dengan
kata lain jumlah arus pada simpul sama dengan nol.
Perkatan masuk dalam hal ini adalah arus yang mengalir menuju simpul
atau menjauhi/keluar dari simpul. Arus yang menuju simpul di asumsikan
positif dan yang keluar dari simpul adalah negatif.
Secara matematik dapat dituliskan :
 i simpul / node  0
…………………………………………………(7)
Perhatikan Gambar 7 misalnya, dapat dituliskan persamaan berikut :
I1 + I4 = I2 + I3
4 + 8 = 2 + 10
12 = 12
(Ampere)
Gambar 7. Hukum Kirchhoff tentang arus
Rangkaian listrik I by Zaenab Muslimin
50
Contoh 1
Tentukanlah arus I3 dan I4 pada Gambar 8 dengan menggunakan hukum
Kirchhoff.
Gambar 8. Contoh 1
Contoh 2
Tentukanlah besar arus I3,I4,I6 dan I7 dan arahnya pada Gambar 9 dengan
menggunakan hukum Kirchhoff.
Gambar 9.Contoh 2
5. Aturan Pembagi Arus
Aturan pembagi arus akan menentukan bagaimana arus pada
masing-masing cabang yang terhubung paralel,
Rangkaian listrik I by Zaenab Muslimin
51
Dua elemen yang besarnya sama terhubung paralel akan
menghasilkan arus yang sama pula.
Untuk elemen yang terhubung paralel dengan besar yang
berbeda akan menghasilkan arus yang lebih besar untuk nilai
R yang kecil.
Arus input I = V/RT, dimana RT adalah resistansi total dari cabang-cabang
paralel. Substitusi V= IX RX dalam persamaan di atas, dimana IX
menunjukkan arus yang mengalir pada cabang paralel dari resistansi RX
maka;
I
I R
V
 X X
RT
RT
Untuk arus I 1  I 1 
dan
IX 
RT
I …………………………(8)
RX
RT
R
I ; untuk arus I 2  I 2  T I
R1
R2
Gambar 10. Pengembangan persamaan pembagi arus
Untuk kasus tertentu dimana dua resistor terhubung paralel seperti pada
Gambar 10, diperoleh :
RT 
I1 
R1 R2
R1  R2
R1 R 2
R
R  R2
dan I 1  T I  1
I
R1
R1
R2
R1
I dan I 2 
I
R1  R2
R1  R2
Rangkaian listrik I by Zaenab Muslimin
……………………………..(9)
52
Contoh 3
Tentukanlah arus I1,I2,dan I3 untuk rangkaian seperti pada Gambar 11.
Gambar 11. Contoh 3
Contoh 4
Tentukanlah resistansi R1 untuk rangkaian seperti pada Gambar 12.
Gambar 12. Contoh 4
6. Sumber Tegangan Hubung Paralel
Sumber tegangan ditempatkan paralel seperti pada Gambar 13
jika keduanya memiliki tegangan nominal yang sama. Alasan utama untuk
menempatkan dua atau lebih baterei terhubung paralel pada tegangan
terminal yang sama adalah untuk meningkatkan arus nominal dari sumber
dengan demikian daya juga bertambah. Seperti pada Gambar 13,dimana
arus nominal dari kombinasi ditentukan oleh IS = I1 + I2 pada tegangan
terminal yang sama. Daya nominal yang diperoleh adalah dua kali dengan
satu suplai.
Rangkaian listrik I by Zaenab Muslimin
53
Gambar 13. Sumber tegangan paralel
Jika dua buah baterei dihubungkan paralel dengan nilai
nominalnya berbeda seperti pada Gambar 14, adalah tidak efektif karena
akan saling mempengaruhi sehingga akan diperoleh tegangan terminal
yang lebih rendah.
Gambar 14. Sumber tegangan paralel dengan nilai yang berbeda
7. Open Circuit (OC) dan Short Circuit (SC)
Dua titik dikatakan hubung buka (open circuit) bila tidak ada
hubungan antara kedua titik tersebut, sehingga rangkaian dapat dikatakan
terputus (lihat Gambar 15a), dengan demikian
a. resistansi antara dua titik besar (∞)
b. tidak ada arus yang mengalir antara dua titik tersebut
Dua titik dikatakan terhubung singkat (short circuit) bila kedua titik tersebut
dihubungkan bersama dengan suatu penghantar yang memiliki resistansi
sangat rendah ( ≈ 0) (lihat Gambar 15b), dengan demikian
a. tegangan pada titik tersebut V= I 0 = 0 volt
b. arus yang mengalir pada titik tersebut sangat besar (IHS)
Rangkaian listrik I by Zaenab Muslimin
54
Gambar 15. Konfigurasi (a) open circuit; (b) short circuit
Perhatikan Gambar 16, tegangan pada terminal open circuit
adalah sama dengan tegangan suplai, tetapi arus yang mengalir sama
dengan nol karena rangkaian terbuka. Sedangkan Gambar 17(a), arus
yang melalui tahanan 2Ω adalah 5A. Jika tahanan 2Ω di hubung singkat
maka diperoleh resistansi total sama dengan 0, dengan demikian arus
akan besar. Arus maksimum ini hanya dibatasi oleh circuit breaker atau
fuse yang seri dengan sumber.
Gambar 16. Demonstrasi karakteristik open circuit
Gambar 17. Demonstrasi pengaruh short circuit terhadap arus
Rangkaian listrik I by Zaenab Muslimin
55
Contoh 5
Tentukanlah tegangan Vab dan Vcd rangkaian Gambar 18.
Gambar 18. Contoh 5
Jawab
Gambar 19. Penyederhanaan gambar contoh 5
Contoh 6
Tentukanlah tegangan dan arus yang tidak diketahui untuk rangkaian
Gambar 20.
Gambar 20. Contoh 6
Rangkaian listrik I by Zaenab Muslimin
56
Gambar 21. Penyederhanaan gambar contoh 6
Rangkaian listrik I by Zaenab Muslimin
57