11.2.1 matriks dan transformasi vektor linier

BAB 11
TRANSFORMASI LINIER
11.1 TRANSFORMASI LINIER
DEFINISI
Pandang 2 buah himpunan
A dan B. Kemudian dengan suatu aturan/cara
tertentu f, kitta mengaitkan atau menggandengkan atau mengkawankan setiap x є
A dengan satu dan hanya satu y є B. Dikatakan : terdapat suatu fungsi f : A →
B.
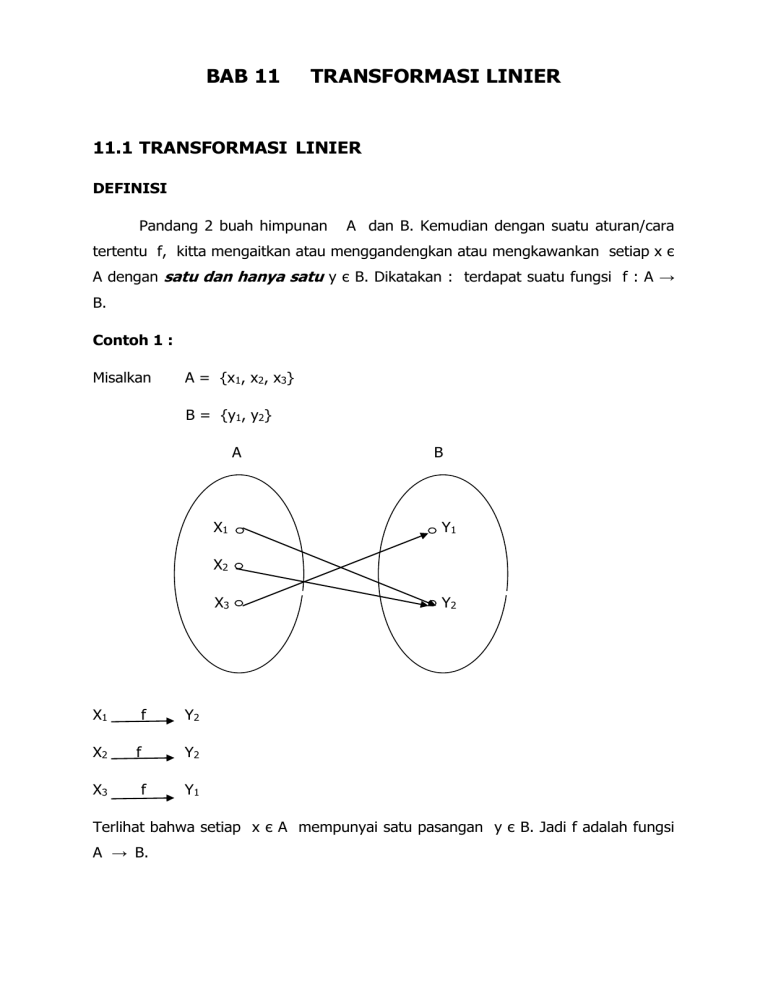
Contoh 1 :
Misalkan
A = {x1, x2, x3}
B = {y1, y2}
A
X1
B
Y1
X2
X3
X1
X2
X3
f
f
f
Y2
Y2
Y2
Y1
Terlihat bahwa setiap x є A mempunyai satu pasangan y є B. Jadi f adalah fungsi
A → B.
Contoh 2 :
Misalkan
A = {x1, x2, x3}
B = {y1, y2}
A
B
X1
Y1
X2
X3
Terlihat bahwa tidak semua
Y2
x є A
mempunyai pasangan. Jadi bukan fungsi.
mempunyai
pasangan, di sini X 2 tidak
Contoh 3 :
Misalkan
A = {x1, x2, x3}
B = {y1, y2}
A
X1
B
Y1
X2
X3
Y2
Terlihat bahwa terdapat x є A di sini X1 mempunyai lebih dari satu pasangan, Y1 dan
Y2 є B. Jadi juga bukan fungsi.
Catatan 1 :
Apabila himpunan A dan B di atas merupakan himpunan bilangan riil R1 (atau
kompleks C1) atau himpunan bagiannya, cara/aturan pengaitan umumnya
dapat dirumuskan dalam suatu hubungan matematis.
Catatan 2 :
Fungsi f : R1 → R1 dimana setiap x є R1 dikaitkan dengan kuadratnya є R1
atau x є x2 atau f(x) = x2 untuk setiap x bilangan riil atau juga y = x2.
Catatan 3 :
Himpunan A di atas disebut
DOMAIN Dan himpunan B di atas disebut
CODOMAIN dari fungsi f tersebut.
Yang menjadi pokok pembicaraan
di dalam bab ini adalah fungsi-fungsi dimana
DOMAIN Dan CODOMAIN nya merupakan RUANG VEKTOR, pada khususnya adalah
Rn, ruang vektor yang anggota-anggotanya n-tupel berurutan bilangan riil (tetapi
sedikit-sedikit disinggung pula Cn atau ruang vektor lain. Untuk ini, kita memilih
menggunakan perkataan lain yaitu TRANSFORMASI atau MAPPING atau PEMETAAN
sebagai penganti perkataan fungsi .
Contoh 4 :
Diketahui suatu transformasi T : R3 → R3 dengan rumus transformasi T[x1, x2, x3] =
[2x1 – x2, x2+x3, x32], untuk setiap x = [x1, x2, x3] є R3. Vektor [2,1,-1] akan
ditransfomasikan oleh T menjadi : T[2,1,-1] = [2.2-1, 1-1, (-1)2] = [3,0,1]
Kita katakan : vektor [3,0,1] adalah peta dari vektor [2,1,-1], sebaliknya : vektor
[2,1,-1] adalah prapeta dari vektor [3,0,1].
Contoh lain :
T[1,2,3] = [0,5,9]
T[4,-1,7] = [9,6,49]……….dst.
11.2 TRANSFORMASI VEKTOR LINIER
DEFINISI
T : V → W suatu transformasi dari ruang vektor V ke ruang vektor W.
Tranformasi T disebut transformasi vektor linier bila terpenuhi :
1) Untuk setiap v1, v2 є V T(v1)+ T(v2) = T(v1+v2), Dan
2) Untuk setiap v є V dan λ skalar berlaku λT(v) = T(λv)
Contoh :
Diketahui T : R3 → R3 dimana :
T’[x1,x2,x3] = [2x1+x2, x2, x3+1] untuk setiap [x1,x2,x3] є R3.
T adalah transformasi vektor yang tidak linier karena syarat 1), misalnya tak
terpenuhi. Ambil v1 = [1,0,0], v2 = [1,0,1] maka T(v1) + T(v2) = [2,0,1] + [2,0,2]
= [4,0,3], sedang T(v1+v2) =T[2,0,1]=[4,0,2].
Jadi T(v1) + T(v2) ≠ T(v1+v2).
11.2.1
MATRIKS DAN TRANSFORMASI VEKTOR LINIER
Pandang T : Rn → Rm suatu transformasi vektor linier.
{ei}, i = 1,2, …, n, basis natural dari Rn
{εi}, i = 1,2, …, m, basis natural dari Rm
T(e1) , T(e2) , …, T(en) adalah vektor-vektor di Rm sehingga merupakan kombinasi
linier dari {εi}
Misalnya
:
T(e1) = a11 ε1 + a21 ε2 + … + am1 εm
T(e2) = a12 ε1 + a22 ε2 + … + am2 εm
(*)
T(en) = a1n ε1 + a2n ε2 + … + amn εm
DEFINISI
Transpose dari matriks koefisien di atas :
[T]e
a11
a12 ….
a1n
a21
a22 ….
a2n
..
..
….
..
..
..
….
..
am1
am2 ….
berukuran (mxn)
amn
Disebut MATRIKS REPRESENTASI dari transformasi linier T, singkatnya matriks
transformasi dari T, relatif terhadap basis-basis natural {ei} dan {εi}.
Contoh :
T : R3 → R3 ssuatu transformasi linier dimana T[x1, x2, x3] = [x1, 2x2, x1+x3].
Mencari matriks transformasi tak lain daripada mencari peta dari vektor-vektor basis.
(Bila tak disebutkan apa-apa selalu dimaksudkan relatif terhadap basis natural).
T(e1) = T[1,0,0] = [1,0,1] = 1e1 + 0e2 + 1e3
T(e2) = T[0,1,0] = [0,2,0] = 0e1 + 2e2 + 0e3
T(e3) = T[0,0,1] = [0,0,1] = 0e1 + 0e2 + 1e3
[T]ee =
1
0
1
0
2
0
0
0
1
Peta dari [2,3,1] :
1
0
1
2
0
2
0
3
1
0
1
1
3
=
6
3
, atau
[3,6,3]
Catatan :
Suatu sifat transformasi linier yang penting adalah bahwa suatu transformasi
linier ditentukan (tertentu) secara natural tunggal oleh peta dari vektor-vektor
basis. Jadi jika peta dari vektor-vektor basis diketahui maka peta dari
sebarang vektor yang lain dapat ditentukan.
Contoh :
T : R2 → R2 dimana diketahui :
T
[2,1] → [5,-2]
T
[-1,1] → [-1,1]
maka untuk menentukan
transformasi
T tersebut kita mencari matriks
transformasi, kita tulis :
T[2,1] = [5,-2] → 2T[1,0] + 1T[0,1] = [5,-2]…….(**)
T[-1,1] = [-1,1] → -1T[1,0] + 1T[0,1] = [-1,1]
3T[1,0]
= [6,-3]
Jadi T[1,0] = [2,-1], dan dari (**) diperoleh T[0,1] = [1,0]
Jadi matriks [T]ee =
2
1
-1
0
Dan rumus transformasinya :
T
X1
X2
= [T]ee
X1
X2
=
2
1
X1
-1
0
X2
atau : T[x1,x2] = [2x1 +x2, -x1].
=
2x1 + x2
-x1
11.2.2
RUANG PETA DAN RUANG NOL
T : Rn → Rm suatu transformasi linier, belum tentu semua vektor di Rm
menjadi peta dari vektor di Rn.
Contoh :
T : R2 → R3 dimana T[x1,x2] = [x2,0,x1].
Maka vektor [1,1,1] є R3 bukan peta dari vektor manapun di R2. Kalau terjadi
demikian, kita katakan transformasi tersebut tidak onto.
DEFINISI
T : Rn → Rm suatu transformasi linier, maka Im(T) = {w | w = T(v), v є Rn},
suatu himpunan bagian dari Rm, disebut RUANG PETA (IMAGE) dari
transformasi linier T.
Ternyata bahwa Im(T) adalah suatu ruang vektor bagian dari Rm.
Catatan 1 :
Dapat terjadi bahwa 2 vektor atau lebih mempunyai peta yang sama. Bila
terjadi demikian, kita katakan bahwa transformasi tersebut “tidak satu-satu”
(one-one).
Contoh :
T : R2 → R2 dimana T[x1, x2] = [x1+2x2, 2x1+4x2], terlihat bahwa :
T[0, 0]
= [0, 0]
T[2,-1]
= [0, 0]
T[-8, 4]
= [0, 0]
dan lain-lain vektor lagi yang mempunyai peta [0, 0]. Jadi T tidak one-one.
DEFINISI KERNEL
T : Rn → Rm suatu transformasi linier, maka Ker(T) = {v | v є Rn, T(v) = 0},
suatu himpunan bagian dari Rn, disebut RUANG NOL (KERNEL) dari
transformasi linier T.
Ternyata bahwa Ker(T) adalah suatu ruang vektor bagian dari Rn.
Catatan 1 :
Dibedakan antara ruang nol dengan ruang berdimensi nol (yaitu ruang vektor
yang anggotanya hanya vektor nol). Anggota ruang nol, selain 0 mungkin
juga vektor ≠ 0.
Catatan 2 :
Kalau
T
:
Rn → Rn
mempunyai matriks transformasi A (matriks bujur
sangkar) yang singular, T dikatakan transformasi
singular, transformasi dikatakan nonsingular.
yang singular. Kalau A
Catatan 3 :
Kalau A adalah matriks transformasi dari T, maka dimensi IM(T) =
rank(A). Hal ini jelas karena kolom-kolom dari A adalah T(e1), T(e2), . . .,
T(en) yang membentuk ruang kolom dari A. Dengan perkataan lain Im(T) = L
{T(e1), T(e2), . . . , T(en)}, berarti dimensi Im(T) = dimensi L{T(e1), T(e2), . .
., T(en)} = rank(A).
Catatan 4 :
Dimensi Ker(T) = n – rank(A).
Mudah dilihat bahwa bila v є Ker(T) maka T(v) = Av = 0.
Susunan persamaan linier homogen Av=0
mempunyai ruang jawab yang
berdimensi n – rank(A). Dengan perkataan lain : mencari Ker(T) tak lain daripada
mencari jawab susunan persamaan linier homogeny Av = 0.
Contoh :
Diketahui
T : R3 → R3 dimana :
T[x,y,z] = [x+2y+z, 2x+3z, 3x+2y+4z]
Tentukan basis dan dimensi ruang peta dan ruang nol !
Jawab :
Pertama kita tentukan dulu matriks transformasi A :
T[1,0,0] = [1, 2, 3]
T[0,1,0] = [2, 0, 2]
T[0,0,1] = [1, 3, 4]
A = [T]ee =
1
2
1
2
0
3
3
2
4
Rank matriks A (secara kolom) :
1
2
1
2
0
3
3
2
4
1
K21
0
0
(-2)
K31(-1)
K23
1
0
0
(4)
2
-4
1
2
0
1
3
-4
1
3
0
1
Rank(A)= 2. Jadi dimensi Im(T) = 2 dan basisnya dapat diambil {[1,2,3], [0,1,1]}.
T di atas adalah transformasi yang singular.
Untuk mencari Ker(T) :
Misalkan v = [v1, v2, v3] є Ker(T), maka Av = 0 atau :
1
2
1
V1
2
0
3
V2
3
2
4
V3
0
=
0
, dimensi Ker(T) = n – rank(A) = 3 – 2 = 1
0
Kita menghitung jawab susunan persamaan linier homogen di atas :
cukup diambil 2 persamaan yang bebas :
v1 + 2v2 + v3 = 0
2v1 + 0v2 + 3v3 = 0
Ambil 1 parameter, misalnya v2 = λ, maka v1 = -6λ, v3 = 4λ.
Jadi v = λ[-6,1,4] ; Ker(T) mempunyai basis (-6, 1, 4)
Atau Ker(T) = L {[-6, 1, 4]}.
11.2.3
PRODUK TRANSFORMASI
Pandang 2 buah transformasi linier :
T : Vn → Wr
S : Wr → Um
dengan matriks transformasi berturut-turut A Dan B.
(dimensi Vn = n, dimensi Wr = r, dimensi Um = m)
Setiap vektor v є Vn oleh transformasi T dipetakan menjadi w = Av, kemudian
hasilnya w є Wr oleh transformasi S dipetakan menjadi u = Bw = B(Av) = (BA)v.
v є Vn
T
→
T
w є Wr →
u є Um
ST
v → u dapat dipandang sebagai suatu transformasi baru ST, dengan matriks
transformasi BA.
ST disebut produk transformasi dari S dan T.
Contoh :
T : R3 → R3 dengan T[x1,x2, x3] = [2x2+x3, 3x1+x2+x3, x2] dan
S : R3 → R3 dengan S[x1, x2, x3] = [2x1+x2+x3, x1+x3, 2x1+x2+2x3]
Maka produk transformasi ST mempunyai rumus :
(ST)
[x1,
x 2,
x 3]
=
S(T[x1,
x 2,
x3])
=
S[2x2+x3,
3x1+x2+x3,
x 2]
=
[2(2x2+x3)+1(3x1+x2+x3)+1(x2), 1(2x2+x3)+1(x2), 2(2x2+x3)+1(3x1+x2+x3)+2(x2)]=
[3x1+6x2+3x3, 3x2+x3, 3x1+7x2+3x3] dan matriks transformasinya :
[ST]ee =
3
6
3
0
3
1
3
7
3
Jelas [S]ee = B =
[T]ee = A =
2
1
1
1
0
1
2
1
2
0
2
1
3
1
1
0
1
0
dan [ST]ee = [S]ee[T]ee = BA.
Peta dari vektor v = [1, 0, 2] adalah ST[1, 0, 2] = [9, 2, 9]
11.3
LATIHAN
DAN
TUGAS