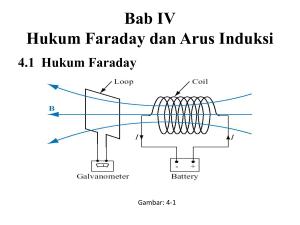
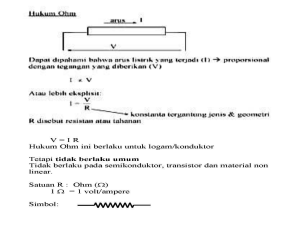
BAB IVA

4.2 Pergerakan Konduktor dalam Medan
Magnet Statis
• Kawat konduktor memuat elektron bebas.
• Gaya Lorentz Fm yang bekerja pada suatu partikel
bermuatan q bergerak dengan kecepatan u di
dalam medan magnet B adalah:
(N)
4-5
Fm  q u  B 
• Bila persamaan di atas dibagi dengan muatan q,
didapatkan gaya per muatan, atau medan listrik
Em yang bekerja pada partikel bermuatan
tersebut, yaitu:
F
Em  m  u  B (V/m)
4-6
q
Gambar: 1
• Tegangan induksi pada kabel:
m
emf
V
 V12   Em  dl   u  B  dl
1
1
2
2
4-7
dimana:
u  B  xˆu  zˆB0   yˆ uB0
dan dl  yˆdl
• Maka:
m
Vemf
 V12  uB0l
4-8
• Secara umum, jika ada segmen sirkuit
tertutup dengan garis C bergerak dengan
kecepatan u melintasi medan magnet statis B,
maka Tegangan induksi emf diberikan oleh:
m
Vemf
  u  B  dl
C
4-9
• Contoh: 1.
Loop persegi ditunjukkan dalam gambar. 4-2
memiliki lebar l konstan, tetapi panjangnya
bertambah xo terhadap waktu dari konduktor
geser bergerak pada kecepatan u dalam
medan magnet serba-sama.
Catatan B meningkat secara linier terhadap x.
Konduktor bergerak mulai dari x = 0 pada
t = 0. Tentukan emf pada konduktor
antara terminal 1 dan 2, dan dihubungkan
dengan rangkaian yang mempunyaii resistor R.
Asumsikan bahwa perlawanan loop R1<<R.
Gambar: 2
• Perhatikan loop 2341, emf yang terjadi pada x
= xo.
m
emf
V
 V12  V43   u  B  dl
4
3
  xˆu  zˆB0 x0  yˆdl  uB0 x0l
4
3
• Dimana: xo = ut
m
emf
V
  B0u lt
2
(V)
(4-10)
• Fluks terjadi:
   B  ds
S
  zˆB0 x   zˆdxdz
S
 B0l 
x0
0
B0lx02
xdx 
2
(4-11)
• Subtitusi xo = ut dalam pers. (4-11), maka:
d
d  B0lu 2t 2 

Vemf     
dt
dt  2 
  B0u 2lt
(4-12)