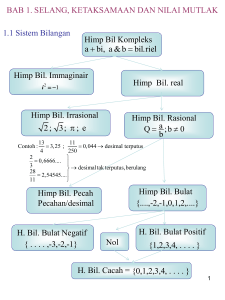
Macam-macam Bilangan

Muhammad Imron H, S.Pd
Sindangkarsa Rt 01/04 No 6
Sukamaju Baru, Tapos, Depok
08562875571
Universitas Gunadarma
 Bilangan Real
 Bilangan Pangkat
 Bilangan Bentuk Akar
 Logaritma
Standart Kompetensi :
Memecahkan masalah berkaitan dengan
Konsep Operasi Bilangan Real
Kompetensi Dasar :
Menerapkan Operasi Pada Bilangan Real
Bilangan Real
Contoh :
1 , 2 , 5 , ½ , -3 , 1000 , 10/9 ,
3 ,
5
•
•
•
•
•
•
•
•
•
Bilangan Asli
Bilangan Ganjil
Bilangan Genap
Bilangan Cacah
Bilangan Rasional
Bilangan Pecahan
Bilangan Khayal(Imajinair)
Bilangan Prima
dll
Bilangan Asli
:
1,2,3,4,5 ...
Bilangan Cacah
:
0,1,2,3,4,5 ...
Bilangan Bulat
:
…,-3,-2,-1, 0,1,2,3,4,5 ...
Bil bulat negatif
Bil bulat positif
Bilangan Pecahan :
…,-½,¼,½,(0,5),25%...
Bilangan Rasional :
…,-1,-½, 0, ¼,1,2...
Bilangan Irrasional:
2,3,5,e,...
Bilangan Rasional adalah
a
Bilangan yang dapat dinyatakan dalam bentuk
b
dengan a dan b bilangan bulat
Bilangan Irrasional adalah
a
Bilangan yang tidak dapat dinyatakan dalam bentuk
b
Bilangan imajinair :
(-1) = i
(-4) = (4).(-1) = 2i
(-25) = (25).(-1) = 5i
Bilangan kompleks :
Contoh :
2+i
3-2i
1+5i
Bilangan dalam Diagram
Bil Kompleks
Bil. Imajinair
Bil. Real
Bil. Rasional
Bil. Pecahan
Bil. Bulat
Bil. Cacah
Nol
Bil. Irrasional
Bil. Bulat Negatif
Bil. Bulat Positif
(Bilangan Asli)
Bilangan dalam Diagram Lingkaran
A = Bil Asli
(-1)
-1
A
½
2
-8
C
0
C = Bil Cacah
B
-5
Q
¼
R
5
K
3i
Q = Bil Rasional
R = Bil Real
K = Bil Kompleks
23
i
(-5)
B = Bil Bulat
RELASI BILANGAN
=,>,<
Contoh :
5 – 2 = 3
>4
2 < 5
7
OPERASI HITUNG
+,-,X,:,pangkat,penarikan akar
Contoh :
3 + 4 = 7
10 - 6 = 4
5 x 2 = 10
30 : 5 = 6
53 = 125
49 = 7
SIFAT-SIFAT OPERASI BILANGAN
1. Tertutup (klosur)
2. Komutatif : a + b = b + a
a x b = b x a
3. Assosiatif :
a +(b + c) = (a + b) + c
a x (b x c) = (a x b) x c
4. Elemen identitas : a + 0 = 0 + a = a
a x 1 = 1 x a = a
0 adalah elemen identitas penjumlahan dan
1 adalah elemen identitas perkalian
5. Elemen invers :
a + (-a) = 0
a x
1
a
= 1
-a adalah elemen invers jumlah dari a
1
adalah elemen invers perkalian dari a
a
6. Distributif :
a x (b + c) = (a x b) + (a x c)
Bilangan Pecahan
a
Bentuk :
b
, b  0
a disebut pembilang
b disebut penyebut
a 1

b 2
belum tentu a = 1 dan b = 2
bisa terjadi a = 5 dan b = 10
Jika :
atau a = 14 dan b = 28
.......dst-nya.
Pecahan Desimal
1 = 0,5
2
13
4
(dibaca : nol koma lima)
= 1,75 (dibaca : satu koma tujuh lima)
atau satu koma tujuh puluh lima perseratus
bukan satu koma tujuh puluh lima
10 1,428571....
7
Bagaimana membacanya ...???
Ubah ke bentuk desimal :
2
9
= 0,2222222….
5
7
= 0,714285714….
7
12
= 0,583333333….
15
26
= 0,576923076….
25
13
= 1,923076923….
Ubah ke bentuk pecahan biasa :
3
0,03 
100
25
1

0,25 
100
4
3
1

0,33333… 
3
9
7
0,777777… 
9
12
4

0,12121212… 
99
33
0,252525….
25

99
123  41
0,123123123…. 
333
999
253
0,253253253.… 
999
3457
0,345734573457…. 
9999
5,10101010….  5 10
2,543543543…. 2
99
543
999
10,001001001…. 10
1
999
Pembulatan Pecahan Desimal
10 1,428571....
7
 1,429
(tiga tempat desimal)
 1,43
(dua tempat desimal)
 1,4
(satu tempat desimal)
0,347613....
 0,3476 (empat tempat desimal)
 0,348 (tiga tempat desimal)
 0,35
(dua tempat desimal)
 0,4
 0,3
(satu tempat desimal)
(satu tempat desimal)
PERSEN
Pecahan dengan penyebut 100 disebut
persen (artinya : per-seratus)
Lambang :
%
Contoh :
3
3 
100
100
X 100% = 3%
3  3
25 25
X 100% = 12%
Nyatakan dalam bentuk persen.
27 
100
2
5
5
4
27%
40%
125%
7 
35%
20
Nyatakan dalam bentuk pecahan biasa :
11
55%
 55
80%
 80  4
100
5
 140  7
5
100
140%
225%
100
 225
100
20
9
4
15% 
15
100
160% 
160
100
3

20
8

5
1). Siswa SMK yang lulus tahun 2009 sebanyak 400 siswa.
a. Jika ada 120 siswa yang melanjutkan ke Perguruan
Tinggi, hitung berapa persen banyaknya siswa yang
tidak melanjutkan ke Perguruan Tinggi ?
b. Jika siswa yang tidak melanjutkan ke Perguruan
Tinggi sebanyak 65%, hitung banyaknya siswa yang
melanjutkan ke Perguruan Tinggi.
2). Tarif kamar hotel Indah pada hari Sabtu dan Minggu
Rp. 250000,-/kamar. Untuk hari Senin dan Selasa
ada potongan 30%, dan pada hari Rabu dan Kamis ada
potongan 25% dan pada hari Jumat potongan 20%.
Berapa tarif kamar pada hari :
a. Senin dan Selasa ?
b. Rabu dan Kamis ?
c. Jumat ?
3). Pak Hasan mempunyai gaji Rp. 2400000,- dan setiap
bulan beliau wajib membayar pajak sebesar 15% dari
gajinya.
a.Berapa besar pajak yang harus dibayar pak Hasan ?
b.Berapa gaji bersih Pak Hasan ?
4). Keluarga pak Amir makan disebuah restoran. Harga
makanan yang dipesan Rp. 160000,-. Pajak yang
dikenakan untuk pembeli di restoran itu sebesar 10%.
a. Berapa rupiah pajak yang harus dibayar pak Amir ?
b. Jika pak Amir membayar dengan 2 lembar uang
seratusribu-an, berapa uang kembalian yang
diterima pak Amir ?
5). Pada penerimaan pegawai suatu perusahaan terdapat
800 orang pelamar. Yang memenuhi kriteria untuk
mengikuti test hanya 720 orang. Setelah diadakan
test yang diterima hanya 1 dari peserta test.
20
a.Berapa orang peserta test yang diterima ?
b.Berapa persen pelamar yang diterima ?
6). Sebuah Departemen Store memberikan diskon 20%
untuk semua barang.
a. Jika harga suatu barang Rp. 65000,-, berapa
harga barang setelah mendapat diskon ?
b. Jika harga suatu barang setelah mendapat diskon
Rp. 32000,-, berapa harga barang sebelum
mendapat diskon ?
BENTUK BAKU
Kecepatan cahaya : 18000000000 m/menit
Masa mol air : 0,00000000000000000000003 gr
Untuk mempermudah penulisan ditulis dalam
bentuk baku :
a x
n
10
Untuk 1  a  10 dan n є Bil. Bulat
Contoh :
1000 000
= 106 (satu juta/miliun)
1000 000 000 = 109 (satu miliar/biliun)
1000 000 000 000 = 1012 (satu triliun)
57 600 = 57,6 x 103 (bukan bentuk baku)
= 5,76 x 104 (bentuk baku)
0,00017= 17 x 10-5 (bukan bentuk baku)
= 1,7 x 10-4 (bentuk baku)
664,83  6,65 x 102
(bentuk baku pembulatan sampai dua tempat desimal )
LATIHAN
Nyatakan bilangan berikut ke dalam
bentuk baku sampai dua tempat desimal :
1). 34,2
2). 50700
3). 17580000
4). 0,00666
5). 0,000796
6). 0,00000000153
Ubah bilangan berikut ke dalam bentuk
desimal :
1). 1,7840 x 10-2
2). 5,99 x 10-5
3). 9,0345 x 105