Sifat-sifat nilai mutlak - elista:.

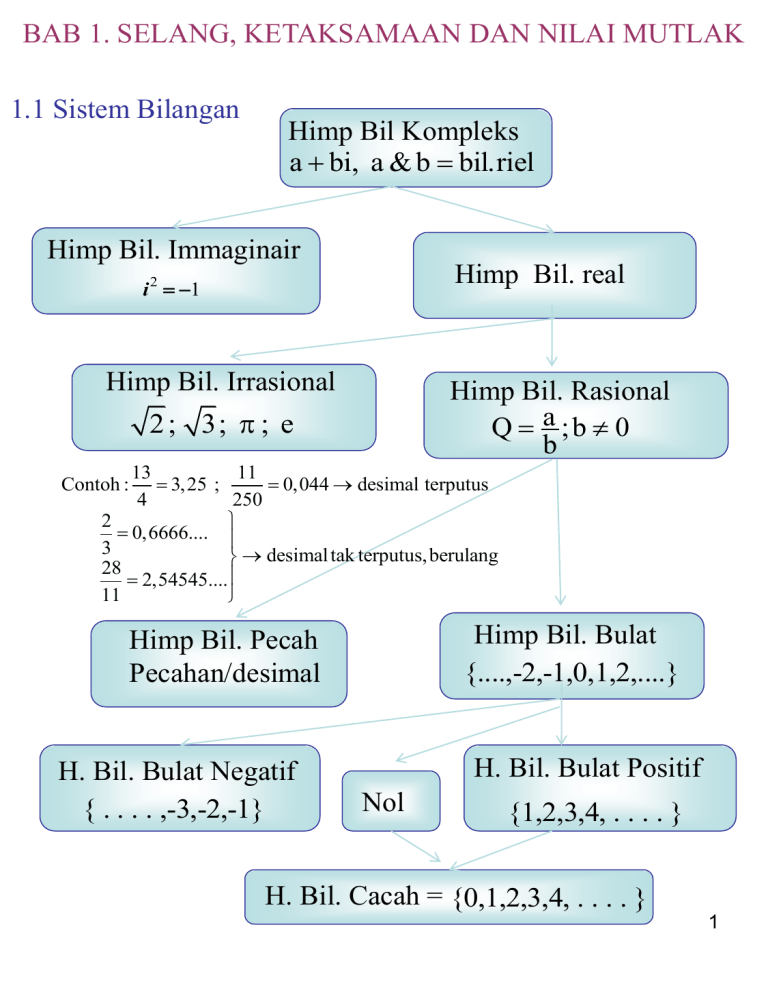
BAB 1. SELANG, KETAKSAMAAN DAN NILAI MUTLAK
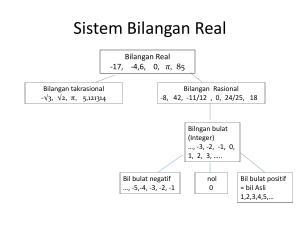
1.1 Sistem Bilangan
Himp Bil Kompleks
a  bi, a & b  bil.riel
Himp Bil. Immaginair
Himp Bil. real
i 2  1
Himp Bil. Irrasional
Himp Bil. Rasional
Q  a ;b  0
b
2 ; 3;  ; e
13
11
 3,25 ;
 0,044  desimal terputus
4
250
2

 0,6666.... 
3
  desimal tak terputus,berulang
28
 2,54545....
11

Contoh :
Himp Bil. Bulat
{....,-2,-1,0,1,2,....}
Himp Bil. Pecah
Pecahan/desimal
H. Bil. Bulat Negatif
{ . . . . ,-3,-2,-1}
H. Bil. Bulat Positif
Nol
{1,2,3,4, . . . . }
H. Bil. Cacah = {0,1,2,3,4, . . . . }
1
Contoh bil rasional :
13
11
 3, 25 ;
 0,044  desimal terputus
4
250
2

 0,6666.... 
3
  desimal tak terputus, berulang
28
 2,54545....
11

Contoh bil irrasional :
2  1, 4142135..... 

3  1, 4422496..... 
  desimal tak terputus tak berulang
  3,1415926..... 
e  2,7182818..... 
1.
Notasi dari himpunan bilangan riil adalah 
 dinyatakan sebagai garis lurus
x є  dibaca x (sembarang bilangan) anggota dari 
Jika x є  dinyatakan sebagai suatu titik di garis

x
Bilangan x terletak antara -a dan a dengan titik pusatnya 0
x
x
-a
0
a
2
2. Urutan Pada Garis Bilangan Riil 
Misalkan: x < y dibaca x berada di sebelah kiri y
atau x lebih kecil dari y
x > y dibaca x berada di sebelah kanan y
atau y lebih kecil dari x
x<y
x
y
x>y
y
x


 dibaca “ jika dan hanya jika”
x < y  y-x positif
3. Sifat urutan
Misalkan x, y, z є 
a. Trikhotomi : Jika x dan y suatu bilangan, maka berlaku
x  y atau x  y atau x  y
b. Transitif: jika x  y dan y  z , maka x  z
c. Penambahan: x  y  x  z  y  z
d. Perkalian: untuk z bilangan positif , x  y  xz  yz
untuk z bilangan negatif x  y  xz  yz
e. Relasi urutan  dibaca “kurang dari atau sama dengan”
 dibaca “lebih dari atau sama dengan”
x  y  y  x positif atau nol
3
4. Sifat-sifat lain
Misalkan a,b,c є , maka berlaku
a. Jika a < b dan c > 0, maka ac < bc
b. Jika a < b dan c < 0, maka ac > bc
c. Jika 0 < a < b, maka 1/a > 1/b
5. Selang (interval)
Definisi: Selang adalah himpunan bilangan real tertentu
yang didefinisikan dan dilambangkan sebagai berikut:
Penulisan Penulisan himpunan
Grafik
(a,b)
{x є  | a < x < b}
a
b
[a,b]
{x є  | a ≤ x ≤ b}
a
b
[a,b)
{x є  | a ≤ x < b}
a
b
(a,b]
{x є  | a < x ∞ b}
a
b
(a,∞)
{x є  | x > a}
[a, ∞)
{x є  | x ≥ a}
(-∞,b)
{x є  | x < b}
b
(-∞,b]
{x є  | x ≤ b}
b
(-∞, ∞)

a
a
4
6. Ketaksamaan (pertidaksamaan)
Definisi: Ketaksamaan adalah pernyataan matematik yang
memuat salah satu relasi urutan <, >,  atau 
Penyelesaian ketaksamaan adalah semua bilangan real yang
memenuhi ketaksamaan tersebut.
dengan sifat urutan
Menyelesaikan ketaksamaan:
dengan garis bilangan
bertanda
Contoh:
1. Dengan menggunakan sifat urutan tentukan penyelesaian
ketaksamaan berikut.
a. -2 < 1 – 5x
b. x2 + 4x = 5
Penyelesaian:
a. 2 x  1  5 x  3x  1
 x1
3
b. x 2  4 x  5  x 2  4 x  5  0
 x 2  1x  5 x  5  0
 x( x  1)  5( x  1)  0
 ( x  5)( x  1)  0

( x  5)  0  x1  5
( x  1)  0  x2  1
5
2. Dengan menggunakan garis bilangan bertandaselesaian
ketaksamaan berikut
2
x
b.  2 x  4  0
3 x
x 1
x

d.
x
x 1
Jawab: (garis bilangan digambar kan di lembar tersendiri)
5
a.  2  5  2 x  x  52
x
2  2x  4
x
b.
 0  x2  2 x  4  0
3 x
a. 5  2
x
5
x5

1

c. x
2x  4
2  4  16
 1 5
2
2  4  16
x2 
 1 5
2
c. 5  1  x  5  5  x  x  5
x
2x  4
x
2x  4
 ( x  5)(2 x  4)  x( x  5)

2x  4  x

x  4
 x1 
d. x  1  x
x
x 1
 ( x  1)( x  1)  x 2
 x2  1  x2
tidak punya penyelesaian
6
7. Nilai Mutlak
Definisi: Nilai mutlak sebuah bilangan real x є 
dinyatakan |a|,
adalah jarak dari x ke 0 pada garis bilangan riil.
4 4
4  4

-4
0
4
Maka berlaku:
| x | x ; jika x  0
| x |  x ; jika x  0
Sifat-sifat nilai mutlak
Misalkan a, b,x є  dan n є , maka
1. | ab || a || b |
a |a|
2.

b |b|
n
n
3. | a || a | dan | x |2  x 2
4. Ketidaksamaan segitiga : | a  b |  | a |  | b |
| a  b | | a |  | b |
5. | x | a   a  x  a
6. | x | a 
x  a atau x  a
7.
| x |  | y |  x2  y 2
8.
| x | a  x  a
7
Contoh (1):
Selesaikan pertidaksamaan berikut:
a. | x  4 |  1,5
b. | 3x  5 |  1
Penyelesaian:
a.
| x  4 |  1,5   1,5  x  4  1,5

2,5
2,5  x  5,5
2,5  x  5,5
5,5
Jadi himpunan penyelesaiannya adalah 2,5  x  5,5
b. Pertidaksamaan | 3x  5 |  1 dapat dinyatakan sebagai:
3x  5   1 atau
3x  5  1
3x  4
atau
3x  6
x 
atau
x  2
4
3
0
1
2
3
 , 43   2,  
4
5

Jadi himpunan penyelesaiannya adalah , 4    2,  
3
8
Contoh (2): [sifat 7]
Selesaikan pertidaksamaan
| 3 x  1|  2 | x  6 |
Penyelesaian:
Menggunakan sifat 7 diperoleh:
| 3 x  1|  2 | x  6 | 
| 3 x  1|  | 2 x  12 |

(3 x  1) 2  (2 x  12) 2
 9 x 2  6 x  1  4 x 2  48 x  144
 5 x 2  54 x  143  0
 (5 x  11) (x  13)  0
untuk (5 x  11) (x  13)  0 diperoleh titik-titik:
5 x  11  0  x1  11
5
x  13  0  x2  13
 , 13
-13
 13, 115 
 115 , 
11
5
Diambil titik-titik uji 14 ; 0 dan 3 , ditemukan titik-titik


didalam 13, 11
yang memenuhi pertidaksamaan tersebut
5
diatas .
9
x2  | x |
8. Akar kuadrat :
Contoh : 1.
9 3
2. (10)2  100 = 10
3. Dua akar kuadrat dari 7 adalah  7
Rumus Kuadrat :
Penyelesaian untuk persamaan ax 2  bx  c  0 adalah
b  b2  4ac
x
2a
Soal:
Tentukan penyelesaian persamaan dan ketaksamaan berikut.
1. | x  2 |  1
2. | x |   x
3. | 4 x  9 |  11
4. | 5 x  4 |  6
6. | x |  | 3  2 x |
7. | 2 x  4 |  | x |  3
10