SISTEM BILANGAN DAN PERTIDAKSAMAAN

SISTEM BILANGAN DAN
PERTIDAKSAMAAN
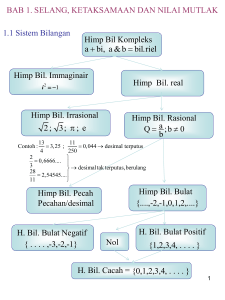
SISTEM BILANGAN
 Bilangan
Asli
Dinyatakan dengan 1, 2, 3, ... biasanya digunakan untuk
menghitung banyaknya benda.
 Bilangan Cacah
0, 1, 2, 3, ...
 Bilangan Bulat
Terdiri dari bilangan bulat negatif, nol dan bilangan bulat
positif. ...-3, -2, -1, 0, 1, 2, 3, ...
 Bilangan Rasional
Bilangan yang dapat dinyatakan dengan a/b dimana b≠0, a, b
ϵ bilangan bulat; (a,b)=1. Bilangan rasional/ pecahan
1 , 1 , 3 ,...
3 2 8
 Bilangan
Irasional
Misalnya . 2, 3, 5,...
Bilangan rasional dan irasional membentuk bilangan real
 Bilangan Kompleks
Bilangan Kompleks
Bilangan yang dibentuk dari bilangan real dan bilangan
imajiner (akar pangkat genap dari bilangan negatif).
Bilangan Asli
Bilangan Bulat
Bilangan Rasional
Bilangan Real
Bilangan Kompleks

Tiap bilangan rasional dapat dinyatakan dalam bentuk
bilangan desimal dengan cara pembilang dibagi oleh penyebut.
Contoh:
1
 0,125
8
1
 0,333...
3
3
 0, 428571428571....
7
2  1, 41421...
Bil.desimal tidak berulang, bil.rasional
Bil.desimal berulang 
Bil.desimal berulang, bil.rasional
Bil.desimal tidak berulang, bil.irasional
1.
Sifat-sifat medan
a. Hukum Komutatif
x + y = y + x dan xy = yx
b. Hukum Asosiatif
x + (y + z) = (x + y) + z dan x(yz) = (xy)z
c. Hukum distribusi
x(y +z) = xy + xz
d. Elemen-elemen identitas
terdapat dua bilangan real yang berlainan 0 dan
1 yang memenuhi x+0 = x dan x.1 = x
e. Balikan (invers)
setiap bilangan x mempunyai balikan
penambahan, -x yang memenuhi x + (-x) = 0. juga
setiap bilangan x kecuali 0 mempunyai balikan
perkalian x-1, yang memenuhi x. x-1 =1
2.
sifat-sifat Urutan
a. Trikotomi
jika x dan y adalah bilangan-bilangan, maka
pasti salah satu berlaku x < y atau x = y
atau x > y
b. Ketransitifan
x < y, dan y < z → x < z
c. Penambahan
x<y↔x+z<y+z
d. Perkalian
bilamana z positif, x < y ↔ xz < xy
bilamana z negatif, x < y ↔ xz > xy
ME
PERTIDAKSAMAAN

Pertidaksamaan satu variabel adalah suatu bentuk aljabar
dengan satu variabel yang dihubungkan dengan relasi urutan.
Penulisan Himpunan
Penulisan Selang
Grafik
{x|a < x < b}
(a, b)
a
b
{x|a ≤ x < b}
[a, b)
a
b
{x|a < x ≤ b}
(a, b]
{x|a ≤ x ≤ b}
[a, b]
a
b
{x|x ≤ b}
(-∞, b]
a
b
{x|x < b}
(-∞, b)
{x| x ≥ a}
[a,∞)
{x|x > a}
(a,∞)
R
(-∞,∞)
b
b
a
a
MENYELESAIKAN SUATU PERTIDAKSAMAAN


Menyelesaikan suatu pertidaksamaan adalah mencari
semua himpunan bilangan real yang membuat
pertidaksamaan berlaku. Himpunan bilangan real ini
disebut juga Himpunan Penyelesaian (HP). Himpunan
penyelesaian suatu pertidaksamaan biasanya terdiri dari
suatu selang bilangan atau gabungan beberapa selang
bilangan.
Cara menentukan HP:
a.
Tambahkan, kalikan bilangan yang sama pada kedua
ruas. Bila mengalikan dengan bilangan negatif maka
tanda pertidaksamaan dibalik arahnya.
b.
Gambarkan titik-titik pemecah tersrbut pada garis
bilangan, kemudian tanda (+, -) pertidaksamaan di
setiap selang bagian yang muncul.
CONTOH:
Tentukan himpunan penyelesaian:
x2-x-6<0
(x-3)(x+2)<0
+
+
-
-2
3
x 1
0
x2
Jawab :
x 1
0
x2
x  2 atau x  1
+
+
-2
1
Latihan
Tentukan himpunan penyelesaian pertidaksamaan berikut :
1.  2  1  5 x  3
2.7 x  1  10 x  4
3.2 x 2  5 x  3  0
x2
4.
2
x4
5.( x  2)(2 x  1)(3 x  7)  0