Fisika Dasar - FMIPA Personal Blogs

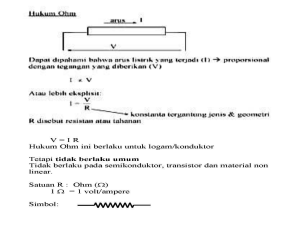
FI1201 Fisika Dasar IIA
Rangkaian Arus Searah
1
Dosen: Agus Suroso
Arus Listrik
Misal terdapat sepotong kawat konduktor berbentuk tabung dengan luas penampang A dan
panjang l. Di dalam potongan kawat tersebut terdapat N partikel bermuatan, dengan muatan
masing-masing q. Sehingga muatan total yang terkandung dalam potongan kawat itu adalah
Q = N q. Didefinisikan rapat jumlah partikel bermuatan per satuan volume sebagai
n=
N
.
Al
(1)
Lalu didefinisikan kuat arus listrik yang mengalir pada konduktor sebagai
I=
dengan vd ≡
dl
dt
dQ
d(N q)
dl
=
= nqA = nqAvd ,
dt
dt
dt
(2)
disebut sebagai laju alir dari partikel bermuatan dalam bahan. Dapat juga
didefinisikan rapat arus yang melalaui konduktor sebagai
J=
I
= nqvd .
A
(3)
Dengan mempertimbangkan arah gerak partikel bermuatan, maka laju alir partikel dapat diperumum menjadi kecepatan alir ~vd , sehingga besaran rapat arus menjadi vektor
J~ = na~vd ,
(4)
dan hubungan antara rapat arus dengan kuat arus listrik dapat ditulis sebagai
~ = I,
J~ · A
(5)
~ menyatakan vektor luasan yang ditembus oleh aliran muatan.
dengan vektor A
~
Mengalirnya muatan dalam bahan konduktor disebabkan oleh adanya medan listrik (E)
di dalam konduktor. Semakin besar medan listrik yang diterapkan, maka laju alir partikel
bermuatan semakin besar, sehingga menurut persamaan (3) rapat arus juga semakin besar.
Kita dapat menuliskan kesebandingan tersebut dalam bentuk
J = σE,
(6)
dengan konstanta kesebandingan σ disebut sebagai konduktivitas listrik dari bahan konduktor.
Semakin besar nilai konduktivitas bahan artinya semakin mudah arus listrik mengalir dalam
bahan tersebut.
2
Hukum Ohm
Dengan mengingat hubungan antara medan listrik dengan beda potensial listrik antara kedua
ujung konduktor (V ) sebagai E =
V
l
dan menuliskan rapat arus sebagai kuat arus per satuan
luas, persamaan terakhir dapat ditulis sebagai
I
V
=σ ,
A
l
1
(7)
versi 29/02/2016, pk. 18:54:40
atau ditulis ulang menjadi
l
= IR,
(8)
σA
menyatakan hambatan (resistansi ) bahan. Hubungan ini disebut sebagai hukum
V =I
dengan R ≡
l
σA
Ohm.
Pada bagian sebelumnya, kita telah mendefinisikan konduktivitas (σ) sebagai besaran yang
menyatakan ukuran ’kemudahan” suatu bahan untuk dialiri arus listrik. Maka besaran kebalikannya ( σ1 ), akan menyatakan besaran yang menyatakan ukuran ’kesulitan’ bahan untuk
dialiri arus. Besaran tersebut disebut resistivitas dan disimbolkan sebagai ρ. Dengan definisi
baru ini, hambatan bahan dapat dituliskan sebagai
l
R=ρ .
A
(9)
Bahan-bahan yang hambatannya mengikuti pola ini disebut sebagai bahan yang bersifat Ohmik.
3
Energi
Pada bagian sebelumnya, terlihat bahwa arus listrik terjadi akibat muatan yang digerakkan
oleh beda potensial antara kedua ujung konduktor. Saat beda potensial sebesar V diberikan,
maka akan timbul medan listrik sebesar E pada bahan. Medan listrik kemudian mempengaruhi
muatan dan menghasilkan gaya pada muatan sebesar F = QE = QV /l. Dari hukum Newton,
diketahui bahwa gaya akan menimbulkan percepatan pada muatan, sebesar a = F/m. Lalu,
percepatan tersebut akan mengubah nilai laju alir vd , dan akhirnya mengubah nilai kuat arus
I. Dari analisis ini, terlihat bahwa beda potensial yang diterapkan pada kedua ujung konduktor akan mengubah nilai kuat arus I. Hal ini tentu tidak sesuai dengan hukum Ohm pada
persamaan (8) yang menyatakan bahwa V yang konstan akan menghasilkan I yang konstan
juga.
Kita dapat mengatasi konflik di atas dengan memandang bahwa di dalam konduktor muncul
gaya hambat (semacam gaya gesek pada mekanika) yang melawan gaya elektrostatik akibat
beda potensial. Besar gaya hambat tersebut (kita sebut Fhambat ) sama dengan gaya elektrostatik
namun berlawanan arah. Dengan adanya gaya hambat ini, maka muatan dalam konduktor akan
mengalami kesetimbangan dan bergerak dengan laju konstan. Besar usaha yang dilakukan oleh
gaya hambat saat muatan mengalir sejauh l adalah
Whambat = Fhambat l = QV.
(10)
Dan daya yang dihasilkan oleh gaya hambat tersebut adalah
P ≡
dW
dQ
=
V = IV.
dt
dt
(11)
Dengan mempehatikan hukum Ohm, daya dapat juga dituliskan sebagai P = I 2 R = V 2 /R.
Kita dapat memandang daya tersebut sebagai laju dilepaskannya energi oleh muatan yang
bergerak. Saat muatan berada dalam medan listrik maka ia akan bergerak dipercepat, sehingga
2
energi kinetik muatan akan bertambah. Namun saat muatan bergerak dalam bahan, gaya
hambat akan melawan perubahan energi kinetik tersebut sehingga energi kinetik muatan tetap
konstan (yang berarti laju muatan konstan).
4
4.1
Hukum Kirchoff
Hukum I Kirchoff
Hukum I Kirchoff menyatakan bahwa jumlah aljabar arus yang menuju suatu percabangan
pada rangkaian listrik akan sama dengan jumlah aljabar arus yang meninggalkannya.
4.2
Hukum II Kirchoff
Hukum II Kirchoff menyatakan bahwa beda potensial total pada suatu lintasan tertutup pada
rangkaian bernilai nol.
3