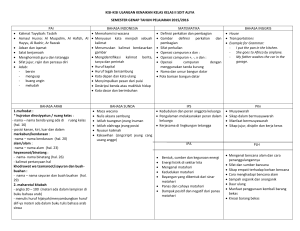
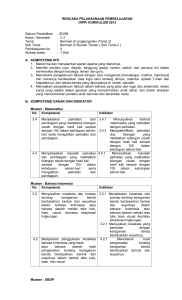
Pengertian Perkalian Matriks Perkalian Matriks yaitu suatu operasi biner yang dapat menghasilkan suatu matriks dari dua matriks dengan entri dalam suatu medan tertentu, atau secara lebih umum dalam suatu gelanggang atau bahkan suatu semigelanggang Sifat – Sifat Perkalian Matriks Perkalian Matariks juga mempunyai beberapa sifat tertentu yaitu sebagai berikut : Sifat komutatif terhadap penjumahan : A + B = B + A Sifat assosiatif terhadap penjumlahan : (A + B) + C = A + ( B + C) Sifat matriks nol : A + 0 = A Sifat lawan matriks : A + (-A) = 0 Sifat asoasiatif terhadap perkalian : (AB) C = A (BC) Sifat distributif kiri : A(B + C) = AB + AC Sifat distributif kanan : (A+B) C = AC + BC Sifat perkalian dengan konstanta : k(AB) = (kA)B = A (kB), dimana k konstanta real Sifat perkalian dengan matriks satuan : AI = IA = A