PDF Bab 2. Persamaan Parametrik dan Sistim Koordinat Kutub compress

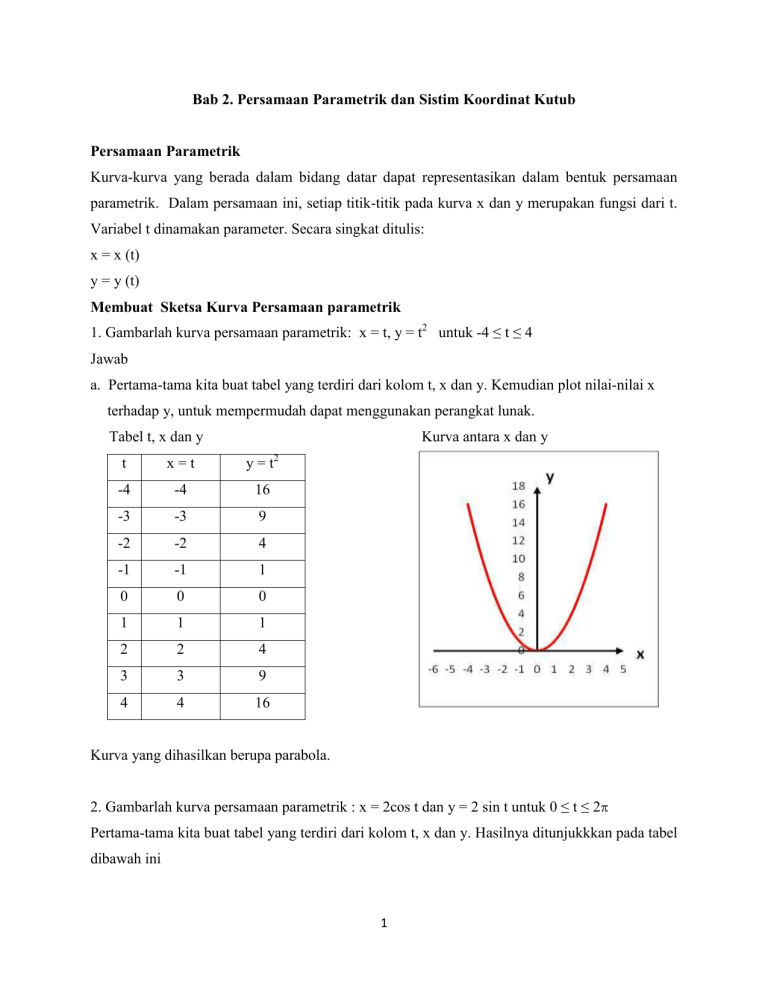
Bab 2. Persamaan Parametrik dan Sistim Koordinat Kutub
Persamaan Parametrik
Kurva-kurva yang berada dalam bidang datar dapat representasikan dalam bentuk persamaan
parametrik. Dalam persamaan ini, setiap titik-titik pada kurva x dan y merupakan fungsi dari t.
Variabel t dinamakan parameter. Secara singkat ditulis:
x = x (t)
y = y (t)
Membuat Sketsa Kurva Persamaan parametrik
1. Gambarlah kurva persamaan parametrik: x = t, y = t2 untuk -4 ≤ t ≤ 4
Jawab
a. Pertama-tama kita buat tabel yang terdiri dari kolom t, x dan y. Kemudian plot nilai-nilai x
terhadap y, untuk mempermudah dapat menggunakan perangkat lunak.
Tabel t, x dan y
Kurva antara x dan y
t
x=t
y=t
-4
-4
16
-3
-3
9
-2
-2
4
-1
-1
1
0
0
0
1
1
1
2
2
4
3
3
9
4
4
16
2
Kurva yang dihasilkan berupa parabola.
2. Gambarlah kurva persamaan parametrik : x = 2cos t dan y = 2 sin t untuk 0 ≤ t ≤ 2
Pertama-tama kita buat tabel yang terdiri dari kolom t, x dan y. Hasilnya ditunjukkkan pada tabel
dibawah ini
1
Tabel nilai t, x dan y
t
x
y
t
x
0.00
3.0000
0.0000
3.36
-2.9287 -0.6500
0.12
2.9784
0.3591
3.48
-2.8299 -0.9960
0.24
2.9140
0.7131
3.60
-2.6903 -1.3276
0.36
2.8077
1.0568
3.72
-2.5120 -1.6401
0.48
2.6610
1.3853
3.84
-2.2976 -1.9290
0.60
2.4760
1.6939
3.96
-2.0502 -2.1902
0.72
2.2554
1.9782
4.08
-1.7732 -2.4199
0.84
2.0024
2.2339
4.20
-1.4708 -2.6147
0.96
1.7206
2.4576
4.32
-1.1472 -2.7720
1.08
1.4140
2.6459
4.44
-0.8071 -2.8894
1.20
1.0871
2.7961
4.56
-0.4554 -2.9652
1.32
0.7445
2.9061
4.68
-0.0971 -2.9984
1.44
0.3913
2.9744
4.80
0.2625
-2.9885
1.56
0.0324
2.9998
4.92
0.6184
-2.9356
1.68
-0.3270
2.9821
5.04
0.9653
-2.8404
1.80
-0.6816
2.9215
5.16
1.2984
-2.7045
1.92
-1.0264
2.8189
5.28
1.6129
-2.5296
2.04
-1.3565
2.6758
5.40
1.9041
-2.3183
2.16
-1.6671
2.4942
5.52
2.1679
-2.0737
2.28
-1.9537
2.2766
5.64
2.4006
-1.7992
2.40
-2.2122
2.0264
5.76
2.5987
-1.4989
2.52
-2.4389
1.7470
5.88
2.7594
-1.1771
2.64
-2.6305
1.4425
6.00
2.8805
-0.8382
2.76
-2.7842
1.1172
6.12
2.9601
-0.4874
2.88
-2.8979
0.7759
6.24
2.9972
-0.1295
3.00
-2.9700
0.4234
6.28
3.0000
-0.0096
3.12
-2.9993
0.0648
6.28
3.0000
0.0024
3.24
-2.9855 -0.2947
2
y
Dalam menyajikan data-data nilai t, buatlah selisih antara nilai t cukup kecil supaya diperoleh
kurva yang smooth. Makin kecil, kurva makin smooth.
Kurva yang dihasilkan
Kurva yang dihasilkan berbentuk lingkaran.
3. Gambarlah kurva persamaan parametrik : x = cos t dan y = 2 sin 2t untuk 0 ≤ t ≤ 2
t
0.00
0.20
0.40
0.60
0.80
1.00
1.20
1.40
1.60
1.80
2.00
2.20
2.40
2.60
2.80
3.00
3.20
3.40
x
0.000000
0.198669
0.389418
0.564642
0.717356
0.841471
0.932039
0.98545
0.999574
0.973848
0.909297
0.808496
0.675463
0.515501
0.334988
0.14112
-0.05837
-0.25554
y
0.000000
0.389418
0.717356
0.932039
0.999574
0.909297
0.675463
0.334988
-0.05837
-0.44252
-0.7568
-0.9516
-0.99616
-0.88345
-0.63127
-0.27942
0.116549
0.494113
t
3.60
3.80
4.00
4.20
4.40
4.60
4.80
5.00
5.20
5.40
5.60
5.80
6.00
6.20
6.40
3
x
-0.44252
-0.61186
-0.7568
-0.87158
-0.9516
-0.99369
-0.99616
-0.95892
-0.88345
-0.77276
-0.63127
-0.4646
-0.27942
-0.08309
0.116549
y
0.793668
0.96792
0.989358
0.854599
0.584917
0.22289
-0.17433
-0.54402
-0.82783
-0.98094
-0.97918
-0.82283
-0.53657
-0.1656
0.23151
Kurva yang dihasilkan:
y
1.5
1.0
0.5
X
0.0
-1.5
-1.0
-0.5
-0.5
0.0
0.5
1.0
1.5
-1.0
-1.5
Mengubah Persamaan Parametrik Menjadi Persamaan Kartesian
1. Ubahlah persamaan parametrik ke dalam bentuk kartesian
a. x = t - 1, y = t2
b. x = 2cos t dan y = 2 sin t
Jawab
1. a. persamaan parametrik :
x=t–1  t=x+1
 y = (x + 1)2 = x2 + 2x + 1
y = t2
persamaan kartesian :
y = x2 + 2x + 1
Ini adalah persamaan kuadrat, kurvanya berupa parabola
b. persamaan parametrik : x = 2cos t dan y = 2 sin t
cos t 
sin t 
x
2
y
2
persamaan identitas: sin2t + cos2t = 1
 y  x
    1
 2 2
2
2
x2  y2  4
Ini adalah persamaan lingkaran yang berpusat di (0, 0) dan berjari-jari 2
4
Mengubah Persamaan Kartesian Menjadi Persamaan Parametrik
1. Tentukan persamaan parametrik dari persamaan kartesian xy = 9
Jawab
Misal x  3t
xy  9  3ty  9  y 
3
t
Jadi persamaan parametrik: x  3t , y 
3
t
Catatan: bisa saja satu bentuk persamaan kartesian memiliki bentuk parametrik lebih dari satu.
Coba pikirkan, kenapa?
2. Tentukan persamaan parametrik dari persamaan kartesian y  6 x 1  x2
Jawab
Misal x = sin
y  6sin  1  sin 2 
y  6sin  cos
y  3sin 2
Jadi persamaan parametrik: x = sin, y = 3sin2
Atau
Misal x = cos
y  6cos  1  cos2 
y  6cos  sin 
y  3sin 2
Jadi persamaan parametrik: x = cos, y = 3sin2
3. Tentukan persamaan parametrik dari persamaan kartesian 9 x2  16 y2  144!
5
Jawab:
9 x2  16 y2  144
x2 y2

 1 Bandingkan dengan cos2 + sin2 = 1
16 9
x2
 cos 2 
16

x  4cos 
y2
 sin 2 
9

y  3sin 
Jadi persamaan parametrik: x = 4cos, y = 3sin
Latihan
1. Gambarkan sketsa grafik persamaan parametrik berikut ini
a. x = 2t, y = t + 4, -2 ≤ t ≤ 3
b. x = 3t – 1, y = 3t2 + 2, -4 ≤ t ≤ 4
c. x = 3t, y = t2-3 untuk-3 ≤ t ≤ 3
d. x = 3t2, y = t3 untuk-3 ≤ t ≤ 3
2
e. x  t  4 , y  1 2 t 3 , untuk-3 ≤ t ≤ 3
3
f. x  t  2t  4 , y  t  1 , untuk-2 ≤ t ≤ 2
2
g. x  t , y 
1
untuk-3 ≤ t ≤ 3
t ,
h. x  4sin  , y  4cos  , untuk 0 ≤  ≤ 2
i. x  5cos  , y  3sin  , untuk 0 ≤  ≤ 2
j. x  sec , y  tan  , untuk-3 ≤  ≤ 3
k. x = cost - 2cos2t,
y = sint - 2cost sint, untuk -0 ≤ t ≤ 2
l. Persamaan Lemniscate Bernoulli
6
Untuk 0 ≤ t ≤ 2
m. x = 31cost - 7cos 31/7t, y = 17sin t – 7sin31/7t, untuk 0 ≤ t ≤ 14
n. x = 17cost + 7cos17/7t, y = 17sin t – 7sin17/7t, untuk 0 ≤ t ≤ 14
o. x = cost + 1/2cos7t + 1/3sin17t, y = sin t + 1/2 sin 7t + 1/3cos17t, untuk 0 ≤ t ≤ 2
2. Tentukanlah bentuk kartesian dari persamaan parametrik berikut ini
a. x = t + 4, y = 1-2t
b. x = t + 1, y = t2 - 2
3
y  4t
t,
c. x 
d. x = t2, y = t3
e. x = t2-1, y = t3 + 2
f. x = t2, y 
g. x 
2
t
1 t
1 t
y
,
t
t
h. x = 3cos, y = 4sin
i. x = sin, y = cos2
j. x = 3cos, y = 5cos2
k. x = 3sec, y = 3tan
l. x 
1 t
2t
y
,
1 t
1 t
3. Tentukan persamaan parametrik dari persamaan kartesian berikut ini
a. y  x 4  x2 , misal x= 2cos 
7
b. y 
x
1 x
2
2
, gunakan 1 + tan2 = sec 
3 1  x2
c. y 
, gunakan x = sin atau x = 1/t
x
4., Sederhanakan x2  y2  6 x  4 y  12  0 kedalam bentuk ( x   )2  ( y   )2  1 kemudian
ubah kedalam bentuk persamaan parametrik
5. Sederhanakan 9 x2  4 y2  18x  16 y  43  0 kedalam bentuk
( x   )2 ( y   )2

1
a2
b2
kemudian ubah kedalam bentuk persamaan parametrik
6. Dengan mensubtitusi y = tx, tunjukkan bahwa persamaan kartesian x3  y3  3xy dapat
dikonversi menjadi persamaan parametrik x 
3t 2
3t
y

1 t3
1 t ,
7. Ambil contoh kasus gerak parabola seperti di ilustrasikan, gerak ini dapat diuraikan menjadi
dua komponen yaitu dalam arah x/horizontal dan dalam arah y/vertikal.
y
vo

x
Berdasarkan konsep-konsep fisika, tentukan persamaan parametrik untuk
menentukankedudukan x dan y.
8
SISTIM KOORDINAT KUTUB
Dalam bagian ini, kita akan mempelajari koordinat kutub dan hubungannya dengan koordinat
kartesian. Koordinat polar menunjukkan posisi relatif suatu titik terhadap sumbu polar dan titik
kutub O (0,0). Titik pada koordinat kutub dinyatakan jari-jari dan sudut.
P (r, )
r
Koordinat kutub :
P (r, )

O
r : jarak dari O ke P (arah dari O menuju P)
 : sudut antara sumbu x dan garis OP
x
Dalam sistim koordinat polar titik asal O dinamakan kutub (pole) dan sumbu x dinamakan
sumbu kutub (polar axis).
Setiap titik pada koordinat kartesius diperoleh dari perpotongan antara x dan y, sedangkan titik
pada koordinat polar merupakan titik potong antara jari-jari lingkaran yang berpusat pada titik
kutub dan garis arah sudut.
Sistim Koordinat Kartesian
Sistim Koordinat Kutub
9
Koordinat Kutub
Sekarang kita belajar menyatakan posisi suatu titik dalam koordinat polar. Perhatikanlah
beberapa contoh titik-titik dibawah ini
y
3 B
/4
3/4
C
D
2
A
1
-3
x
-2
-1
2
1
3
-1
E
-2
5/4
F
7/4
-3
Dalam gambar diatas ada dua lingkaran yang kecil berjari-jari 2 dan yang besar berjari-jari 3.
Dan juga terdapat dua garis lurus yang menunjukkan sudut diukur dari sumbu polar.
Titik A terdapat pada lingkaran kecil (r=2) dengan sudut /4 sehingga dapat dinyatakan
A (2, /4)
Titik B terdapat pada lingkaran besar (r=3) dengan sudut /2 sehingga dapat dinyatakan
B (3, /2). Coba lanjutkan untuk titik C, D, E dan F sebagai latihan.
Konversi koordinat kutub ke koordinat kartesius
y
Kartesius ke Kutub
P (r, )
y
r
r2 = x2 + y2
 = tan-1 (y/x)

O
x
x
10
Kutub ke Kartesius
x = r cos 
y = r sin
Contoh:
1. Ubahlah titik-titik dibawah ini ke bentuk kutub
a. (-3,-4)
b. (5,- 7)
2. Ubahlah titik-titik dibawah ini ke bentuk kartesius
a. (2, 1/3)
b. (-3, 4/3)
Jawab
a. Dari titik (-3, -4) diperoleh x = -3 dan y = -4
r2 = x2 + y2
= (-3)2 + (-4)2
= 25
r=5
 = tan-1(4/3) = 233o
 Kartesius: (-3, -4), kutub: (5, 233o)
b. Dari titik (5, -7) diperoleh x = -3 dan y = -4
r2 = x2 + y2
= (5)2 + (-7)2
= 25+ 49
= 71
r =
71
 = tan-1(-7/5) = 305,54o
Kartesius: (5, -7), kutub: ( 71 , 305,54o)
2.
a. Dari titik (2, 1/3) diperoleh r = 2 dan  = 1/3
x = r cos 
= 2 cos1/3
= 2  1/2
=1
11
y = r sin 
= 2 sin1/3
= 2  1/2
=
3
3
Kutub (2, 1/3), kartesius: (1,
3)
b. Dari titik (-3, 4/3) diperoleh r = -2 dan  = 4/3
x = r cos 
= -3 cos 4/3
= -3  (-1/2)
= 3/2
y = r sin 
= 2 sin 4/3
= -3  (-1/2 3 )
= 3/2 3
Kutub (-3, 4/3), kartesius: (3/2, 3/2 3 )
Dalam sistim koordinat kartesius, setiap titik dinyatakan oleh x dan y secara spesifik artinya titik
berbeda, maka x dan y nya pun berbeda. Lain halnya dalam sistim koordinat kutub karena r
punya arah dan nilai  punya acuan arah putar dan bersifat periodik sebesar 2 maka untuk titik
yang sama dapat dinyatkan oleh r dan  yang berbeda-beda dengan jumlah representasi tak
berhingga.
y
Perhatikanlah contoh berikut
A
2
1
-3
-2
-1
1
-1
-2
12
/4
2
x
3
Dalam sistim kartesius: A (2, 2)
Dalam sistim kutub:
A (2 2 , /4), A (2 2 , /4 + 2), A (2 2 , /4 + 4),… A (2 2 , /4 + 2n)
Boleh juga
A (2 2 , -7/4), A (2 2 , -7/4+2), A (2 2 , -7/4+4), …A (2 2 , -7/4+ 2n)
Boleh juga
A (-2 2 , 5/4), A (-2 2 , 5/4+2), A (-2 2 , 5/4+4), … A (-2 2 , 5/4+ n2)
Dengan n = 1, 2, 3,…
Mengkonversi persamaan kartesian ke kutub
1. Ubahlah persamaan berikut ke kutub
y = 3x- 8
jawab
ingat: x = r cos dan y = r sin
y = 3x- 8
r sin = 3r cos - 8
r sin - 3r cos = - 8
r (sin - 3 cos) = - 8
r
8
3cos   sin 
2. Ubahlah persamaan berikut ke kutub
x2+ (y - 3)2 = 9
jawab
x2+ (y - 3)2 = 9
x2 + y2 - 6y + 9 = 9
x2 + y2- 6y = 0
r2 – 6 r sin  = 0
13
r(r - 6 sin ) = 0
r - 6 sin  = 0
r = 6 sin 
Mengkonversi persamaan kutub ke kartesian
3. Ubahlah persamaan berikut ke kartesian
r cos = -4
jawab
r cos = -4
x = -4
4. Ubahlah persamaan berikut ke kartesian
r2 = 4r cos
Jawab
r2 = 4r cos
x2 + y2 = 4x
x2 -4x + y2 = 0
x2 -4x + 4 + y2 = 4
(x - 2)2 + y2 = 4
14
Membuat grafik pada sistim koordinat kutub
Buatlah grafik himpunan titik-titik koordinat polar dengan syarat-syarat berikut:
a. r = 2
b. -2 ≤ r ≤ 3
c. r ≤ 0,  = 1/4
d. 1/4 ≤  ≤ 1/6
Jawab
Solusinya ditunjukkan pada gambar dibawah ini
y
y
a.
b.
-3
-2
-3
2
2
1
1
x
-1
1
2
-3
3
-2
x
-1
1
-1
-1
-2
-2
2
3
-3
y
y
/4
c.
2
2
-2
x
-1
/6
1
1
-3
/4
d.
1
2
-3
3
-2
x
-1
1
-1
-1
-2
-2
2
Latihan
1. Manakah titik-titik koordinat polar berikut ini yang menunjukkan titik yang sama
15
3
a. (3, 0)
b. (-3, 0)
c. (2, 2/3)
d. (2, 7/3)
e. (-3,)
f. (2, /3)
g. (-3, 2)
h. (-2, -/3)
2. Plot titik-titik koordinat polar berikut ini
a. (1, /6)
b. (-1, /6)
c. (2, /6)
d. (3, /6)
e. (2, /4)
f. (2, -/4)
g. (3, 5/6)
h. (-3, 10/4)
3. Konversi koordinat kartesius dibawah ini menjadi koordinat polar
a. (3, 4)
b. (-2,
3)
c. (1, -2)
d. (10, - 2 )
e. (-5, 7)
f. (-6, -4 3 )
g. (-8, 6)
h. (12, -5)
4. Konversi koordinat polar dibawah ini menjadi koordinat kartesius
a. ( 2 , /4)
16
b. (0, /2)
c. (-3, 2/3)
d. (- 7 , 5/6)
e. ( 2 3 , -/4)
f. ( 2 , /4)
g. (0, /2)
h. (-3, 2/3)
5. Buatlah grafik dari himpunan titik-titik koordinat polar yang memenuhi syarat berikut ini
a. r = 4
b.  = 2/3, r ≤ -2
c.  = /3, -1 ≤ r ≤ 3
d. r = 2, 0 ≤  ≤ 
e. 1 ≤ r ≤ 2, 0 ≤  ≤ /2
f. -3 ≤ r ≤ 2,  = /4
g. r ≤ 0,  = /4
h. 2/3 ≤ r ≤ 5/6
6. Konversi persamaan polar berikut ini menjadi persamaan kartesius
a. r cos  = 4
b. r sin  = -5
c. r cos  + r sin  = 1
d. r = cot  csc 
e. r = 2cos  + 2 sin 
f. r2 + r2cos  sin  = 1
g. r2 sin 2 = 2
h. r = 2cos  - sin 
7. Konversi persamaan kartesius berikut ini menjadi persamaan polar
17
a. x = 7
b. x - y = 3
c. y = 5
d. x y= 2
e. x2 + y2 = 5
f. x2 - y2 = 1
g. x2 + xy + y2 = 1
18