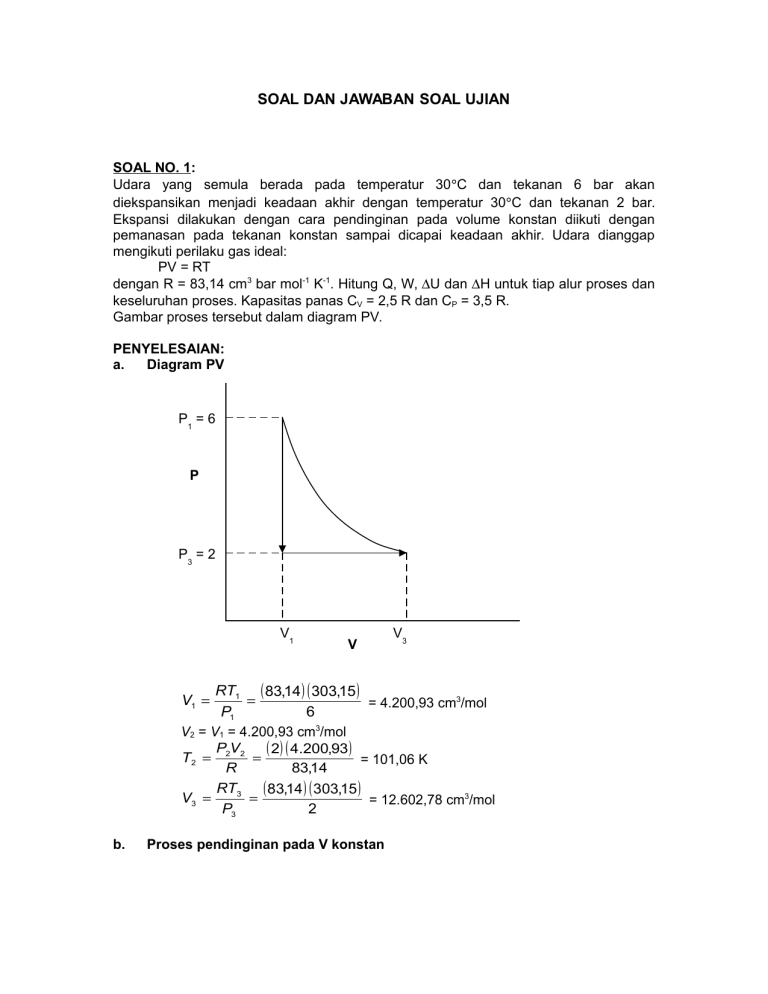
SOAL DAN JAWABAN SOAL UJIAN SOAL NO. 1: Udara yang semula berada pada temperatur 30C dan tekanan 6 bar akan diekspansikan menjadi keadaan akhir dengan temperatur 30C dan tekanan 2 bar. Ekspansi dilakukan dengan cara pendinginan pada volume konstan diikuti dengan pemanasan pada tekanan konstan sampai dicapai keadaan akhir. Udara dianggap mengikuti perilaku gas ideal: PV = RT dengan R = 83,14 cm3 bar mol-1 K-1. Hitung Q, W, U dan H untuk tiap alur proses dan keseluruhan proses. Kapasitas panas CV = 2,5 R dan CP = 3,5 R. Gambar proses tersebut dalam diagram PV. PENYELESAIAN: a. Diagram PV P1 = 6 P P3 = 2 V1 V V3 RT1 83,14 303,15 = 4.200,93 cm3/mol P1 6 V2 = V1 = 4.200,93 cm3/mol PV 2 4.200,93 T2 2 2 = 101,06 K R 83,14 RT3 83,14 303,15 V3 = 12.602,78 cm3/mol P3 2 V1 b. Proses pendinginan pada V konstan V2 W P dV 0 V1 T2 U CV dT CV T1 T2 2,5 83,14 101,06 303,15 T1 = 42.005,1 cm3 bar mol1 Q = U – W = 42.005,1 – 0 = 42.005,1 cm3 bar mol1 T2 H C P dT C P T1 T 2 3,5 83,14 101,06 303,15 T1 c. = 58.807,1 cm3 bar mol1 Proses pemanasan pada P konstan V3 W P dV 2 (12.602,78 4.200,93) = 16.802,04 cm3 bar mol1 V2 T3 Q H CP dT CP T3 T2 T2 = 3,5 (83,14) (303,15 – 101,06) = 58.807,1 cm3 bar mol1 U = Q + W = 58.807,14 16.802,04 = 42.005,1 cm3 bar mol1 d. Keseluruhan proses Q = 42.005,1 + 58. 807,14 = 16.802,04 cm3 bar mol1 W = 0 16.802,04 = 16.802,04 cm3 bar mol1 U = 42.005,1 + 42.005,1 = 0 H = 58.807,1 + 58.807,1 = 0 SOAL NO. 2 Udara sebanyak 0,03 kg mengalami proses siklis seperti pada gambar di bawah. Hitung kerja/usaha yang dapat dihasilkan dari sistem tersebut, Udara dianggap mengikuti perilaku gas ideal, CV = 2,5 R dan CP = 3,5 R. Berat molekul udara rata-rata adalah 28,84. 100 kPa V 0,002 m PENYELESAIAN 3 0,02 m3 30 1,04 mol 28,84 20 L V3 V2 19,24 l mol 1,04 mol 2L V1 1,924 l mol 1,04 mol n Titik 3: P3 V3 nRT3 T3 1 bar 19,24 l mol 231,3 K P3 V3 0,08314 l bar K mol R Hubungan antara titik 1 dan 3 C 3,5 P 1,4 C V 2,5 P1 V1 P3 V3 V P1 P3 3 V1 19,24 1 1,924 1, 4 = 25,12 bar P1V1 nRT1 T1 P1V1 25,12 bar 1,924 l mol 581 K nR 0,08314 l bar K mol Titik 2 T2 = T1 = 581 K Usaha yang dihasilkan: V2 V2 V1 V1 W12 n P dV 1,04 mol RT dV V 1,04 mol RT1 ln 2 V V1 1,04 mol 0,083141 l bar K mol 581 K ln 19,24 = – 115,7 l bar 1,924 V3 W23 n P dV 0 V2 W31 U 31 C V T1 T3 2,5 0,083141 l bar K mol 581 231,1 K 72,7 l bar Wtotal W12 W23 W31 115,7 0 72,7 40,1 l bar SOAL NO. 3 Gas nitrogen berada di dalam tangki yang volumenya 4 m3, tekanannya 42 bar, dan temperaturnya 30C. Hitung massa gas nitrogen tersebut. Gas nitrogen dianggap mengikuti persamaan keadaan SRK. Untuk menghitung volume molar nitrogen, lakukan iterasi sebanyak 2 kali. PENYELESAIAN Tc = 126,19 K Pc = 33,978 bar = 0,04 Z3 Z 2 A B B 2 Z AB 0 Pr Tr2 P B b r Tr A a 1 0,48508 1,55171 0,15613 2 1 Tr0,5 2 T 303,3 2,402 Tc 126,19 P 42 Pr 1,236 Pc 33,978 Tr 1 0,48508 1,55171 0,04 0,15613 0,04 2 1 2,4 0,5 = 0,4889 2 Pr 0,4895 1,236 0,42747 = 0,0448 2 Tr 2,4 2 P 1,236 B a r 0,08662 0,0448 Tr 2,4 A a c 0 AB 0,4889 0,0448 0,002 c1 A B B2 0,4889 0,0448 0,04482 0,00179 c 2 1 f Z Z3 c 2 Z 2 c1 Z c0 f ' Z 3Z 2 2c 2 Z c1 f Zi Zi1 i1 f 'i1 Tebakan awal: Z0 = 1 Iterasi 1 f0 = 1 – 1 – 0,00179 (1) – 0,002 = – 0,00378 f’0 = 3 (1) + 2 (– 1) (1) – 0,002 = 0,99821 f 0,00378 Z1 Z 0 0 1 1,0134 f '0 0,99821 Iterasi 2 f1 = (1,01342) – 1,013422 – 0,00179 (1,01342) – 0,002 = 2,88 10-5 f’1 = 3 (1,01342)2 + 2 (– 1) (1,01342) – 0,00179 = 1,01342 Z1 Z 0 f0 2,88 10 5 1 1,0038 f '0 1,01342 i Z(i) 0 1 1.0037 92 1.0037 63 1.0037 63 1 2 3 f(i) -0.00378 2.88E-05 1.63E-09 -9.3E-17 f'(i) 0.9982 1 1.0134 2 1.0133 06 1.0133 06 error 0.0150 09 0.0001 13 6.37E09 SOAL NO. 4 Udara yang semula berada pada temperatur 30C dan tekanan 1 bar akan dikompresi menjadi keadaan akhir dengan tekanan 5 bar melalui proses kompresi adiabatis. Udara dianggap mengikuti perilaku gas ideal: PV = RT dengan R = 83,14 cm3 bar mol-1 K-1. Hitung Q, W, U dan H. Kapasitas panas CV = 2,5 R dan CP = 3,5 R. Hitung Q, W, U, dan H. PENYELESAIAN P P2 P1 V2 T1 = 303 K P1 = 1 bar P2 = 5 bar C 3,5 R P 1,4 C V 2,5 R Proses adiabatis: TP(1 - )/ = konstan T1 P1(1 - )/ = T2 P2(1 - )/ V1 V P1 P2 T2 T1 1 1 5 303 11, 4 1, 4 479,9 K Q=0 T2 479 , 9 T1 303 T2 479 , 9 T1 303 H CP dT 3,5 RdT 3,5 R 479,9 393 = 304,15 R U CV dT 2,5 RdT 2,5 R 479,9 393 = 217,25 R W = U – Q = 217,25 R