01 Fungsi

1
Fungsi
Fungsi disebut juga pemetaan. Notasi fungsi f : A  B
himpunan A ke himpunan B”.
dibaca “f memetakan
Definisi:
Diberikan dua himpunan tidak kosong A dan B. Fungsi f : A  B adalah relasi antara
himpunan A dan B, di mana setiap elemen di A berelasi dengan tepat sebuah elemen
di B.
Himpunan A disebut daerah asal, domain, atau himpunan prapeta; dan himpunan B
disebut daerah hasil, ko-domain, atau himpunan peta.
Jika x  A , maka peta dari x dinotasikan sebagai f (x) . Sebaliknya, jika f ( x)  y ,
maka prapeta dari y adalah x.
Representasi fungsi
Fungsi f : A  B dapat direpresentasikan dalam berbagai cara. Di antaranya:
 Secara diagram
 sebagai himpunan pasangan terurut {( x, f ( x)) | x  A} . Contoh: f={(1,2), (2,4),
(3,9), (4,16)}
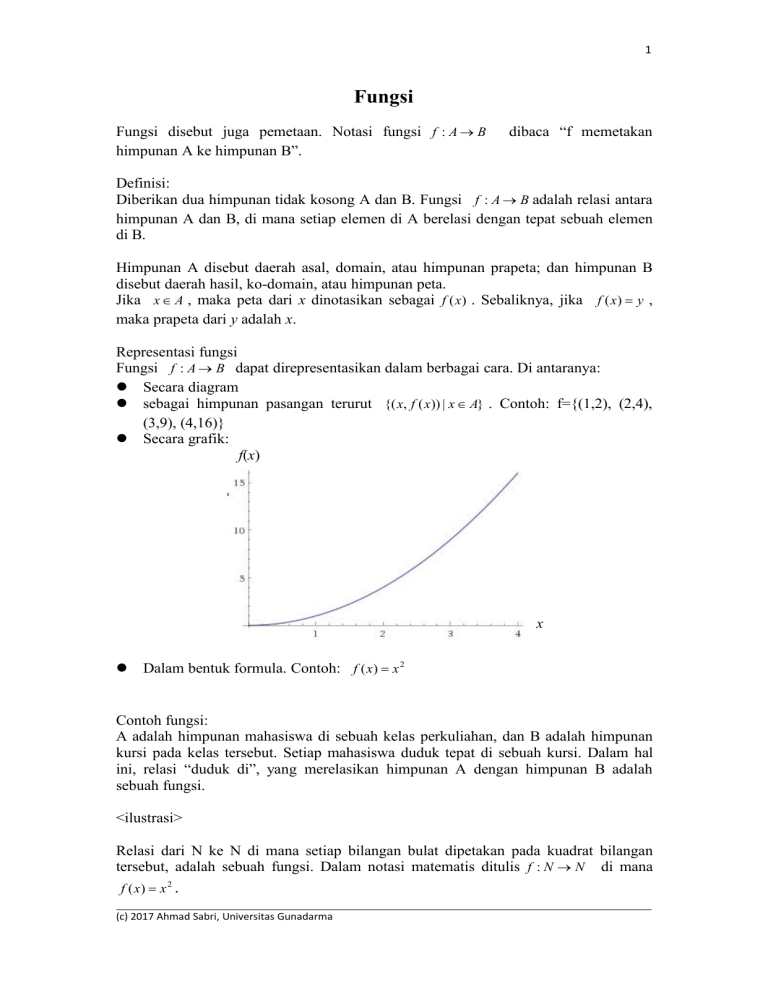
 Secara grafik:
f(x)
x

Dalam bentuk formula. Contoh: f ( x)  x 2
Contoh fungsi:
A adalah himpunan mahasiswa di sebuah kelas perkuliahan, dan B adalah himpunan
kursi pada kelas tersebut. Setiap mahasiswa duduk tepat di sebuah kursi. Dalam hal
ini, relasi “duduk di”, yang merelasikan himpunan A dengan himpunan B adalah
sebuah fungsi.
<ilustrasi>
Relasi dari N ke N di mana setiap bilangan bulat dipetakan pada kuadrat bilangan
tersebut, adalah sebuah fungsi. Dalam notasi matematis ditulis f : N  N di mana
f ( x)  x 2 .
(c) 2017 Ahmad Sabri, Universitas Gunadarma
2
Dalam perkuliahan ini, fungsi yang dipelajari adalah fungsi yang didefinisikan pada
himpunan bilangan riil atau subhimpunannya.
Beberapa himpunan bilangan:
ℝ: himpunan bilangan riil (semua bilangan yang terdapat pada garis bilangan)
ℚ: himpunan bilangan rasional (bilangan yang dapat dinyatakan sebagai pembagian 2
bilangan bulat)
ℤ={…,-2,-1,0,1,2,…} (himpunan bilangan bulat/integer)
ℕ={1,2,3,…} (himpunan bilangan asli/natural)
Perhatikan bahwa ℕ⊂ℤ⊂ℚ⊂ℝ
1. Fungsi berdasarkan sifat relasinya
Ditinjau dari sifat relasinya, fungsi dikategorikan menjadi:
1. Fungsi injektif (satu-satu/one-one)
2. Fungsi surjektif (pada/onto)
3. Bijektif (satu-satu pada/one-one onto)
4. Tidak termasuk salah satu di atas
1.1. Fungsi injektif
Diberikan fungsi f:A→B. Fungsi f adalah injektif jika untuk sebarang x1,x2ϵA, maka
berlaku f(x1)≠f(x2).
Pada fungsi injektif, sebarang dua elemen yang berbeda memiliki peta yang berbeda.
Contoh:
Fungsi f : N  R di mana
3
f ( x)  3 x
adalah injektif karena jika x1  x2
maka
x1  x2
3
1.2. Fungsi surjektif
Diberikan fungsi f : A  B . Fungsi f adalah surjektif jika untuk sebarang y  B ,
maka terdapat x  A sehingga f ( x)  y .
Pada fungsi surjektif, setiap elemen pada ko-domain memiliki prapeta pada domain.
Contoh:
Fungsi f : R  R0 di mana f ( x)  x 2 karena setiap bilangan riil non negatif
memiliki akar bilangan riil. Perhatikan bahwa f tidak injektif karena x dan -x memiliki
peta sama, contohnya f (2)  f (2)  4 .
Q: Apakah fungsi f : N  R , f ( x)  3 x adalah surjektif?
1.3 Fungsi bijektif
Adalah fungsi yang injektif dan surjektif. Pada fungsi bijektif, semua elemen pada
domain memiliki peta yang berbeda, dan semua elemen pada ko-domain memiliki
prapeta yang berbeda.
Contoh:
(c) 2017 Ahmad Sabri, Universitas Gunadarma
3
Fungsi f : R  R di mana f ( x)  x  2 adalah fungsi bijektif.
1.4. Fungsi yang tidak injektif dan tidak surjektif
Contoh: Fungsi f : Z  R0 , f ( x)  x 2 adalah tidak injektif dan tidak surjektif. Tidak
injektif karena terdapat elemen-elemen berbeda dengan peta yang sama, contoh
f ( 2)  f ( 2)  4 . Tidak surjektif karena bilangan pecahan ataupun irasional pada
ko-domain tidak memiliki prapeta (tidak ada kuadrat bilangan bulat menghasilkan
bilangan pecahan).
2. Beberapa fungsi riil dengan karakteristik tertentu
 Fungsi konstanta: f ( x)  k , di mana k  R .
 Fungsi identitas: f ( x)  x .
 Fungsi genap: f ( x)  f ( x) untuk semua x pada domain.
 Fungsi ganjil: f ( x)   f ( x) untuk semua x pada domain.
 Fungsi periodik. f (x) disebut fungsi periodik dengan periode T > 0, jika untuk
setiap x pada domain berlaku f ( x  T )  f ( x) , di mana T adalah konstanta
terkecil yang memenuhi. Contoh: f ( x)  sin x adalah periodik dengan periode
T  2 , karena sin x  sin( x  2 ) .
 Fungsi terbatas:
 f (x) disebut fungsi terbatas di atas pada suatu interval a  x  b bila terdapat
konstanta M sedemikian sehingga f ( x)  M untuk setiap x pada interval
tersebut. Contoh: f ( x)   x 2  2 x adalah fungsi terbatas di atas, karena
f ( x)  1 untuk semua x  R . Fungsi f ( x)  x  2 dibatasi di atas oleh 7
pada interval 0  x  5 .
 f (x) disebut fungsi terbatas di bawah pada suatu interval a  x  b bila
terdapat konstanta m sedemikian sehingga f ( x)  m untuk setiap x pada
interval tersebut. Contoh: f ( x)  x 2  4 x dibatasi di bawah oleh -4, karena
f ( x )  4 untuk semua x  R . Fungsi f ( x)  x  2 dibatasi di bawah oleh
2 pada interval 0  x  5 .
 Fungsi monoton:
 f (x) disebut fungsi monoton naik lemah pada suatu interval a  x  b jika
untuk setiap x1 , x2 pada interval tersebut berlaku f ( x1 )  f ( x2 ) . (Untuk
fungsi monoton naik kuat berlaku f ( x1 )  f ( x2 ) ).
 f (x) disebut fungsi monoton turun lemah pada suatu interval a  x  b jika
untuk setiap x1 , x2 pada interval tersebut berlaku f ( x1 )  f ( x2 ) . (Untuk
fungsi monoton turun kuat berlaku f ( x1 )  f ( x2 ) ).
(c) 2017 Ahmad Sabri, Universitas Gunadarma