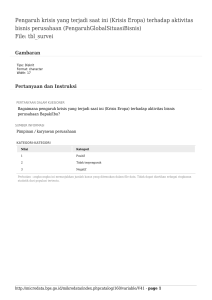
FFT adalah nama algoritma yang paling populer untuk komputasi Transformasi Fourier Diskrit dari suatu sinyal diskrit
x[k]. Hasil dari FFT adalah spektrum magnitud terhadap frekuensi dari suatu sinyal diskrit. Umumnya, suatu sinyal
diskrit/kontinyu terbentuk dari campuran beberapa sinyal dengan frekuensi berbeda. Misalnya, pada kasus bercampurnya sinyal informasi dan noise, FFT dapat membantu kita mengetahui pada frekuensi berapa sinyal informasi berada dan pada frekuensi berapa noise mendominasi.
PERHITUNGAN FFT DI NYATAKAN DENGAN PERSAMAN
Ket
Kerangan:
X(k) adalah hasil transformasi fourier diskrit dari x[k], memuat nilai-nilai magnitud sinyal untuk k = 0,
1, ... N x(k) yang dinyatakan dalam x(j) adalah sinyal waktu diskrit N adalah panjang sinyal x(k
Dalam contoh ini, transformasi Fourier akan digunakan untuk menemukan frekuensi sinyal informasi yang telah bercampur noise. Data di-sampling pada 1000 Hz. Sinyal informasi pada frekuensi
50 Hz memiliki amplitudo 0.7 dan pada 120 Hz amplitudo 1 bercampur dengan noise acak dengan rerata nol.
Kode untuk generate sinyal informasi dan noise
Fs = 1000; % Frekuensi sampling
T = 1/Fs; % Periode sampling
L = 1000; % Panjang sinyal informasi
t = (0:L-1)*T; % Vektor waktu
% Jumlahan sinus 50 Hz dan 120 Hz, sinyal informasi
x = 0.7*sin(2*pi*50*t) + sin(2*pi*120*t);
y = x + 2*randn(size(t)); % Sinyal informasi plus noise
plot(Fs*t(1:50),y(1:50))
title('Signal Corrupted with Zero-Mean Random Noise')
xlabel('time (milliseconds)')
Perhitungan FFT dinyatakan dengan persamaan
Sangat sulit untuk mengenali frekuensi sinyal dengan melihat sinyal aslinya.
Kita perlu mengonversi sinyal ini ke domain frekuensi dengan algoritma FFT.
Kode untuk konversi sinyal ke domain frekuensi dengan fungsi fft MATLAB
NFFT = 2^nextpow2(L);
% NFFT adalah panjang vektor hasil perhitungan FFT. Baiknya adalah bilangan dari angka 2 yang
dipangkatkan, dan sedikit lebih panjang dari sinyal informasi. Sehingga digunakanlah fungsi
nextpow2.
Y = fft(y,NFFT)/L;
% Untuk mendapatkan normalisasi magnitud sinyal, nilai hasil FFT harus dibagi dengan L (panjang
data)
f = Fs/2*linspace(0,1,NFFT/2);
% Vektor frekuensi untuk plot spektrum frekuensi. Pembagi dua pada Fs/2 dan NFFT/2 digunakan
karena vektor Y bersifat simetris. Y(1)=Y(NFFT); Y(2)=Y(NFFT-1); dst. Y(1) untuk frekuensi 0 dan
Y(NFFT) untuk frekuensi 2π. Jadi plot spektrum frekuensi cukup mengambil data Y(1) s.d.
Y(NFFT/2).
% Plot single-sided amplitude spectrum.
plot(f,2*abs(Y(1:NFFT/2)))
title('Single-Sided Amplitude Spectrum of y(t)')
xlabel('Frequency (Hz)')
ylabel('|Y(f)|')
Amplitudo sinyal informasi tidak tepat 0.7 dan 1 karena pengaruh noise. Selain
itu juga karena panjang sinyal x(k) terbatas. Mengubah nilai L dari 1000 ke
10000 pada contoh ini akan menghasilkan nilai amplitudo yang lebih tepat