Memulai Menggunakan Maple

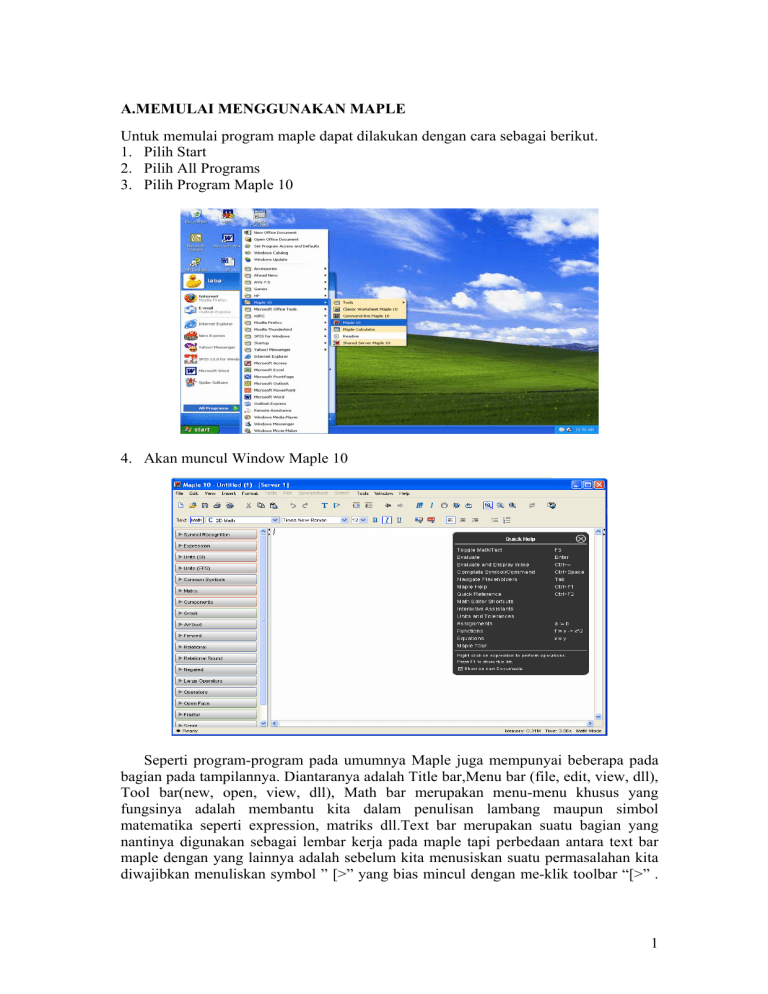
A.MEMULAI MENGGUNAKAN MAPLE
Untuk memulai program maple dapat dilakukan dengan cara sebagai berikut.
1. Pilih Start
2. Pilih All Programs
3. Pilih Program Maple 10
4. Akan muncul Window Maple 10
Seperti program-program pada umumnya Maple juga mempunyai beberapa pada
bagian pada tampilannya. Diantaranya adalah Title bar,Menu bar (file, edit, view, dll),
Tool bar(new, open, view, dll), Math bar merupakan menu-menu khusus yang
fungsinya adalah membantu kita dalam penulisan lambang maupun simbol
matematika seperti expression, matriks dll.Text bar merupakan suatu bagian yang
nantinya digunakan sebagai lembar kerja pada maple tapi perbedaan antara text bar
maple dengan yang lainnya adalah sebelum kita menusiskan suatu permasalahan kita
diwajibkan menuliskan symbol ” [>” yang bias mincul dengan me-klik toolbar “[>” .
1
Perintah ke computer diberikan dengan mengetikkan pada text bar setelah [>. Perintah
ini dicetak dalam warnah merah atau hitam, sedangkan jawaban atau respon akan
dicetak dalam warna biru. Dalam maple setiap perintah harus diakhiri dengan dengan
symbol atau anda titik koma ( ; ) jika hasil atau respon ingin ditampilkan dan symbol
titik dua ( : ) jika ingin respon atau hasil tidak ingin ditampilkan.
B.OPERASI ARITMATIKA
+ dan * dan /
^
Sqrt
Evalf
: Tambah dan kurang
: Kali dan Bagi
: Pangkat
: Akar kuadrat
: Memberikan nilai numeric
Dalam pengoperasiannya, operasi dasar aritmatika menggunakan hukum-hukum
berdasarkan prioritas operasi, misalkan perkalian dioperasikan terlebih dahulu
daripada penjumlahan. Begitupula dengan operasi yang lainnya,
C.KONSTANTA
Konstanta yang sering digunakan oleh maple adalah Pi, E, dan I.
D.FUNGSI
Dalam maple juga fungsi-fungsi diantaranya adalah
E^x
Ln(x)
Sin(x), cos(x), tan(x),csc(x), sec(x),cot(x)
arcsin(x), arccos(x) dll
sinh(x),cosh(x), dll
arcsinh(x), arccosh(x), dll
: Fungsi Eksponensial
: Logaritma Natural
: Trigonometri
: Invers Trigonometri
: Hiperbolik
: Invers Hiperbolik
E.MENDEFINISIKAN VARIABLE DAN FUNGSI
Untuk mendefinisikan suaru variabel harus menyertakan symbol ” := “ (
Keterangan : diantara titik dua dan sama dengan tidak ada spasi ). Mendefinisikan
suatu variabal akan berakibat variable itu akan dipakai terus sampai program atau
pengoperasian selesai. Walaupun pendesinisiannya diganti. Untuk bisa merubah
desinisi suatu fariabel maka dibutuhkan perintah “restart;” pada awal perintah atau
pengoperasian.
2
Contoh
Didefinisikan bahwa A=5 dan B=2 tentukan hasil dari 4*A/B danA^2+B^3
Fungsi juga memerlukan suatu pendefinisian misalnya:
Perintah diatas berfungsi untuk mendefinisikan fungsi f ( x) = 5 x 2 + 4 x − 9 .
Setelah didefinisikan kita bisa memenggil fungsi tersebut dengan perintah “f(x);”
variable x juga bisa diganti, untuk mencari hasil dari fungsi f(x). misalnya f(6), f(3),
f(Pi).
F.MANIPULASI POLINOMIAL
Ada beberapa perintah penting yang biasanya digunakan dalam maple diantaranya
yaitu:
1. simplify
: Untuk menyederhanakan ekspresi aljabar
Contoh:
p:=1-x+(x^2-1)/(1—x);
Jika disederhanakan dengan meggunakan “ simplify“maka:
2. factor
: Memfaktorkan suatu ekspresi
Sedangkan untuk memfaktorkan polynomial kita dapat menggunakan perintah
“factor”
contoh:
q:=y^69-1
3. solve
: Menyelesaikan system pertidaksamaan untuk sekumpulan variable
Contoh 1
Untuk mencari nilai x dari x 3 − 3 x 2 + x − 3 adalah dengan menggunakan perintah
“solve”.
3
solve(x^3-3x^2+x-3);
Keterangan: I adalah bilangan imajiner (akar dari -1).
Cara lain yaitu dengan mendefinisikan terlebih dahulu polinomila tersebut
h:=x-> x^3-3x^2+x-3;
solve(h(x));
Contoh 2
Untuk menyelesaikan system pertidaksamaan 2x+3y=10, 5x-y=3 untuk x dan y,maka:
Solve({2*x+3*y=10,5*x-y=3},{x,y});
Atau kita mendefinisikannya terlebih dahulu:
sistem:={ 2*x+3*y=10,5*x-y=3};
solve(sistem,{x,y});
4. fsolve
: Memberikan solusi numeric
Contoh 1
Fsolve(h(x));
Contoh 2
fsolve(sistem,{x,y});
5. evalf
: Merupakan suatu perintah yang untuk mencari hasil akhir yang lebih
spesifik dan dalam bentuk desimal.
4
Contoh
25/27+3/51;
evalf(25/27+3/51,3) ;
6. expand
: Expansi suatu ekspresi
CONTOH LAIN
sistem:={ 2*x+3*y=10,x^2-y=7};
solve(sistem,{x,y});
fsolve(sistem,{x,y});
Untuk hasil kita bisa memberikan keterangan hasil atau jawaban pada
penyelesaiannya misalnya
Hasil:=fsolve(sistem,{x,y});
Bila ingin memenggil masing-masing hasil yaitu hasil pertama dan kedua bisa kita
ketikkan perintah hasil[1] dan hasil[2].
Hasil[1];
Hasil[2];
G. SUBSTITUSI
Untuk dapat melakukan operasi substitusi terlebih dahulu kita mendefinisikan
suatu ekspresi. Setelah tu kita baru mensubtitusikan variable dengan nilai tertentu
yang kita inginkan.
Contoh
ekspresi:=sin(x)^2+sin(x);
subs(x=eta,ekspresi);
hasil:=evalf(subs(x=Pi/3,ekspresi));
H. MENGHITUNG NILAI LIMIT
Maple juga dapat digunakan untuk mencari penyeleaian dari persoalan yang ada pada
kalkulus salah satunya yaitu mencari atau menghitung nilai limit.
Contoh 1
Limit(cos(x)/x,x=0)= limit(cos(x)/x,x=0);
Contoh 2
h:=x->(1-x)/(x-3)^2
Limit(h(x),x=0)=limit(h(x),x=0);Limit(h(x),x=infinity)=limit(h(x),x=infinity);
Limit(h(x),x=3)=limit(h(x),x=3);
Limit(h(x),x=1)=limit(h(x),x=1);
5
Perhatikan peranan huruf besar L dan huruf keci l pada perintah limit. Sebutkan?
I. MENYELESAIKAN DIFERENSIASI
Maple menggunakan perintah diff untuk mendeferensialkan suatu fungsi
Contoh 1
Diff(h(x),x)=diff(h(x),x);
B:=Diff(h(x),x)=simplify(diff(h(x),x));
subs(x=10,rhs(B))
Keterangan rhs(B) adalah right hand side dari B
Diff(h(x),x$2)=simplify(diff(h(x),x$2));
Turunan Parsial
l:=(x,y)->x^2-3xy^2+5x*x^3*y^4;
Diff(l(x,y),x,y)=diff(i(x,y),x,y);
Sebutkan peranan huruf besar D dan huruf kecil d pada perintah diff?
Perintah Diff(h(x),x$n); merupakan perintah turunan ke-n dari h(x) terhadap x.
J. MENYELESAIKAN PERSOALAN INTEGRASI
Dalam maple untuk menyelesaikan persoalan integrasi menggunakan perintah
Int(fungsi integrand, variable);
Contoh1
Int(h(x),x)=int(h(x),x);
6
Walaupun sedang mengghitung integral taktentu, Maple tidak memunculkan
konstanta sembarang C.
Int(Int(h(x),x),x)=int(int(h(x),x),x);
Int(h(x),x=0..2)=evelf(int(h(x),x=0..2));
INTEGRAL LIPAT DUA
Contoh 2
k:=(x,y)->1+x*y;
Int(Int(k(x,y),y=x..x^2),x=..2)=int(int(k(x,y),y=x..x^2),x=0..2);
Perhatikan peranan huruf I dan i pada Int dan int. sebutkan perbedaan fungsi dan
peranannya. Juga perhatikan perintah evalf.
K. PLOT GAMBAR
Maple mempu menggambar suatu fungsi satu dimensi, dua dimensi atau tiga
dimensi dengan beberapa fasilitas operasi yang lain. Untuk dapat menggunakan
perintah-perintah pengeplotan ini, terlebih dahulu harus memanggil perintah
“with(plot);”
7
Plot ada banyak macamnya diantaranya yang sering dipakai adalah plot 1 dimensi,
3 dimensi atau yang diasanya disingkat dengan3D.
Contoh
Gambarlah persamaan garis y = x^2 + 6 untuk x=1 sampai x=5
Sedangkan untuk plot 3D contohnya adalah
plot3d(sin(x*y), x=-Pi..Pi, y=-Pi..Pi,style=contour);
PLOT OPTION
Dalam plot juga ada beberapa pilihan atau option yang harus diperhatikan yaitu
diantaranya adalah
Color
: Pilihan ini berfungsi untuk menentukan warda dari grafik ayang
akan ditampilkan. Dan dalam pemilihan ini penulisannya
berdasarkan ejaan bahasa inggris. Misalnya ingin membuat grafik
maka warna yang dituliskan adalah “red” jika menginginkan
warna biru maka dapat menggunakan atau mengetik kata “blue”
dan lain-lain.
Style
: Style merupakan suatu pilihan untuk menentukan bentuk dari
gambar atau garafik ayang akan kita buat. Dalam stile ini ada dua
macam yaitu “point” atau “line”. Point di sini artinya adalah
8
bahwa grafik yang dibentuk berupa point atau titik-titik yang
membentuk suatu garis atau kurfa. Sedangkan line yaitu garis
atau kurfa yang akan dibuar berbentuk gasis.
Title
: Agar dapar membedakan antara gambar satu dengan gambar yang
lain maka masing-masing gambar dadat diberi mana sesuai
dengan keperluanya melewati option labels.
Linestyle
: Linestyle merupaka suatu option yang digunakan untuk
menentukan daereah mana yang akan digambar atau biasanya
disebut dengan barasan-batasan suatu daerah
Labels
: Labels berfungsi sebagai nama dari dua hal yang akan
dihubungkan biasanya untuk manamakan label pada sumbu x dan
sumbu y.
L.PERSAMAAN DIFERENSIAL ORDE PERTAMA
Penerapan persamaan diferensial biasa orde pertama bisa diselesaikan dengan
bantuan program aplikasi maple. Persamaan ini dinamakan persamaan diferensial
biasa orde pertama karena persamaan ini hanya mengandung turunan pertama dari
fungsi yang tak diketahi, misalnya y(x) yang akan ditentukan dari persamaan
itu.persamaan ini muncul dalam banyak penerapan biologi, fisika, rekayas dan
penerapan lainnya seperti model matematis dari berbasai system fisisi dan system
lainnya.
Suatu persamaan diferensial orde pertama dikatakan linear jika persamaan itu
dituliskan sebagay berikut
dy / dx + p ( x) y = r ( x )
Ciri khas dari persamaan ini yaitu linear dalam y dan dy/dx, dengan p dan r
merupakan fungsi dari setiap x yang diberikan. Jika ruas sebelah kanan r(x) bernilai
nol maka untuk semua nilai x dalam interval yang ditinjau, maka persamaan ini
dikatakan homogen, sebaliknya dikatakan tak homogen.
Turunan-turunan y’ dinotasikan oleh diff(y(x),x)atau D(y)(x). turunan parsial
diperoleh dengan cara yang sama. Solusi persamaan diferensial dapat diperoleh
dengan perintah dsolve(selesaian persamaan diferensial). Pengeplotan grafik solusi
dapat dilakukan dengan perintah plot(f,h,v,…), dimana f adalah fungsi-fungsi yang
akan diplot, h adalah range horizontal dan v adalah range vertical dan kolom
berikutnya bisa diisi dengan beberapa pilihan tampilan.
Contoh1
dy / dx + y cos( x ) = 1 / 2 * sin( 2 x ), y (0) = 1 .
Restart;
p:=cos(x);
r:=1/2*sin(2*x);
h:=int(p,x)
9
Jadi solusi umum persamaan ini adalah
solum:=y(x)=exp(-h)*(int(exp(h)*r,x)+c);
eval(subs(x=0,y=I,solum));
Misal kita substitusikan c=3 maka
subs(c=3,solum);
Contoh 2 Persamaan Peluruhan Radioaktif, Peluruhan Eksponensial.
Suatu percobaan menunjukkan bahwa suatu unsure radioaktif meluruh laju yang
sebanding dengan banyaknya unsure saat itu. Jika banyakknya unsure yang diberikan
3 gram pada waktu t=0, apa yang terjadi dengan banyaknya unsure yang tersisa
kemudian
Proses fisis ini denyatakan dengan persamaan deferensial orde pertama
dy / dx = ky (t ), y (0) = 3
Dimana k merupakan konstanta fisis yang nilai numeriknya diketahui untuk
berbagai unsure radioaktif. Bila k=-C, C>0 maka persamaan diferensial ini
menyatakan proses peluruhan eksponensial.
Misalnya pers didedinisikan sebagai dy / dx = ky (t ) , maka
restart;
pers:=diff(y(t),t)=k*y(t);
10
Solusi umum yang dilambangkan dengan (sol) didapat dengan melalui perintah dsilve
sol:=dsolve(pers,y(t));
Notasi _Cl untuk menyatakan suatu konstanta sembarang. Dari sol didapat solusi
khusus dengan mensubstitusikan kondisi awal y(0)=3 (yang menunjukkan keadaan
dari system fisis itu).
eval(subs(t=0,y(0)=3,sol));
eval merupakan perintah untuk menghitung. Dengan mensubstitusikan _Cl = 3 , maka
subs(_Cl=3,sol);
solusi khusus juga bisa ditentukan dengan
yp:=dsolve({pers,y(0)=3},y(t));
11
Keterangan : tanda kurung kurawal {..} untuk himpunan dua item (persamaan dan
kondidi awal). Untuk menggambarkan grafik solusi itu, maka bisa mengeplot yp
dengan menentukan suatu niali konstanta k, misalnya k = -0,5 (karena peluruhan).
Sehingga
yp1:=subs(k=-0,5,yp);
plot(rhs(yp1),t=0..5,title=”Grafik Peluruhan Eksponensial”);
12
Contoh 3. Hukum Pendinginan Newton
Bentuk dasar pelurusan eskponensial telah dimodifikasi pada berbagai model fisika.
Sebagai contoh adalah hokum pendinginan Newton sebagai sebuah model kehilangan
panas dari sebuah obyek penginginan. Hukum ini menyatakan bahwa temperatur dari
obyek itu menurun sebanding dengan beda antara temperatur obyek itu dengan
temperatur sekiternya. Laju perubahan temperatur pada sembarang waktu diberikan
oleh persamaan diferensial,
dT/dt=-k(T-T1)
dimana T(t) merupakan temperatur dari onyek pendingin yang diletakkan dalam suatu
medium dengan temperature tetap T1 dan k adalah konstanta perbandingan.
Sebagai contoh, jika sebuah bola tembaga dipanaskan sampai temperature 100
derajat Celcius dan kemudian pada saat t=0 bola itu direndam dalam air yang
bertemperatur tetap 30 derajat Celcius. Setelah 3 menit ternyata temperature bola
menjadi 75 derajat Celcius. Kapankah temperature bola itu menjadi 37 derajat
Celcius?
Masalah ini merupakan fenomena proses penurunan temperature dari sebuah bola
tembaga, sehingga bentuk model matematikanya adalah
dT/dt = - k(T – 30),k>0
T(0) = 100, T(3) = 75
restart;
with(plots);
pers:=diff(T(t),t)=-k(T(t)-30);
sol:=dsolve({pers,T(0)=100},T(t));
Kita akan menghitung besarnya konstanta k dengan menggunakan informasi T(3) =
75.
75=subs(t=3,rhs(sol));
jadi
k:=evalf(1/3*ln(70/45));
Dengan menggunakan nilai k ini, maka temperature bola T(t) adalah:
T(t):=subs(k=.1472775842,rhs(sol));
Selanjutnya temperature T=37 derajat Celcius dicapai ketika
37=T(t);
t=evalf(ln(70/7)/k);
Jadi temperature T = 37 derajat Celcius dicapai pada saat mendekati 46 manit.
plot(T(t),t=0..30,title=”Penurunan Temperatur Bola Tembaga”);
Limit(T(t),t=infinity)=limit(T(t),t=infinity);
Interpretasi hasil ini adalah bahwa penurunan temperature bola tembaga untuk waktu
yang lama menuju ke temperature tetap air.
Contoh 4
Model pertumbuhan kontinu.
Misalkan N(t) menyatakan populasi dari suatu spesies pada waktu t, maka ratarata perubahan pada waktu t
13
dN(t)-dt = kelahiran – kematian + migrasi
Merupakan sebuah persamaan konservasi untuk populasi itu. Model yang
disederhanakan diasumsikan tidak ada migrasi dan besarnya kelahiran dan kematian
adalah proporsional terhadap N. jadi model yang disederhanakan mempunyai bentuk
persamaan diferensial orde pertama
dN(t)/dt = k N(t) – m N(t) dengan kondisi awal N(0)= 10
Dimana k, m adalah konstanta positif. Solusi persamaan ini diselesaikan sebagai
berikut
restart;
pers:=diff(N(t),t)=k*N(t)-m*N(t);
Solusi umum misalkan dinamakan “sol” diperoleh melalui perintah dsolve
sol:=dsolve(pers,N(t));
Dimana _Cl adalah konstanta sembarang.
Misalakan kondisi awal diketahui, N(0)=10, maak solusi khusus untuk masalah syarat
awal ini adalah dengan mencari besarnya _Cl, maka
eval(subs(t=0,N(0)=10,sol));
Dengan mensubstitusikan _Cl = 10 ke dalam sol maka diperoleh subs(_Cl=10,sol);
14
sebenarnya jika tidak tertarik pada solusi umum, solusi khusus Np juga bisa diperoleh
secara langsung yaitu,
Np:=dsolve({pers,N(0) = 10},N(t));
Perilaku pertumbuhan populasi ini dapat diamati pada grafik solusi dengan
memberikan nilai k dan m.
Bila k>m maka populasi bertumbuh secara eksponensial. Misalkan k = 5 dan m = 2.
Np1:=subs(k=5,m=2,Np);
plot(rhs(Np1),t=0..2,title=”Gambar: Grafik Pertumbuhan Eksponensial”);
Bila k<m maka populasi akan punah. Misalkan k = 5 dan m = 6.
Np2:=subs(k=5,m=6,Np);
plot(rhs(Np2),t=0..2,title=”Gambar: Grafik Kepunakan Eksponensial”);
Contoh 5
Model Von Bertalanffy dari Pertumbuhan Ikan
Model klasikal ini menggambarkan panjang ikan sebagai sebuah fungsi umur,
berdasarkan ada asumsi bahwa pertumbuhan ikan sebanding dengan beda antara
panjang dengan panjang maksimum secara teotitis. Persamaan diferensialnya yang
menjelaskan proses ini adalah
15
dL/dt = k(Lm – L)
Di mana L adalah panjang ikan, Lm adalah panjang maksimum secara teoritis
dan k adalah konstanta laju pertumbuhan. Sebagai contoh, DeMarias mempelajari
pertumbuhan ikan air tawar kecil, Buglossidium luteum dalam teluk dari lau
Mediteranea. Sepanjang tahun pertama dari kehidupannya, ikan ini mengikuti model
pertumbuhan Von Bertalanffy, dan mendapatkan penjang 51,6 mm. Dengan
mengasumsikan panjang awal 8,2 mm dan konstanta laju pertumbuhan 0,23 per bulan,
kita akan menyelesaikan parsamaan ini selama satu periode 12 bulan.
restart;
pers:=diff(L(t),t)=0.23*(51.6-L(t);
Lp:=dsolve({pers,L(0)=8.2),L(t});
evalf(limit(Lp,t=infinity));
plot(rhs(Lp), t = 0..12, title=”Gambar :GrafikPertumbuhan Ikan”,axes=BOXED
Hasil ini menunjukkan bahwa penjang maksimumikan adalah 51,6 mm.
Contoh 6. Pemisahan Variabel.
Pada Contoh ini, kita menyelesaikan persamaan diferensial orde pertama dengan
metode pemisahan variable.
Pandang Persamaan diferensial:
dy/dx = -2xy
restart;
pers:=diff(y(x),x)=-2*x*y(x);
sol:=dsolve(pers,y(x));
Dengan memberikan berbagai nilai _Cl pada solusi umum sol, kita mendapatkan
berbagai solusi khusus. Kita akan membuat grafik dengan memberikan empat buah
nilai _Cl yang berbeda dan mengeplot ketiga solusi khusus itu pada sumbu yang sama
dengan perintah
yp0:=subs(_Cl=0.2,sol);
yp1:=subs(_Cl=0.5,sol);
yp2:=subs(_Cl=2,sol);
yp3:=subs(_Cl=3,sol);
16
plot({rhs(yp0), rhs(yp1), rhs(yp2), rhs(yp3)},x=-2..2,title=”Kurva Solusi Berbentuk
Lonceng di ½ Bisang Atas”);
Contoh 7. Modal Pertumbuhan Logistik.
Hukum Malthus menyatakan bahwa bahwa laju pertumbuhansuatu populasi N(t)
berbabanding lurus dengan N(t) saat itu. Pertanyaan ini berlaku untuk beberapa
populasi yang tidak terlalu besar. Model yang lebih baik adalah model pertumbuhan
logistic yang diberikan sebagai
dN/dt = aN – bN^2.(a>0, b>0).
Dimana “syarat-bebas” – bN^2 mengakibatkan populasi itu tidak dapat tumbuh
dalam jangka waktu yang tidak terbatas. Persamaan diferensial ini merupakan sebuah
persamaan Bernoulli khusus dan dinamakan persamaan Verhulst. Selesaikanlah
persamaan ini dan berapakah limit dari N(t) bila t menuju tak hingga?
restart;
persV:=diff(N(t),T)-a*N(t)=-b*N(t)*2;
solum:=Dsolve(persV,N(t),explicit);
Untuk menggambar beberapa solusi, kita bias ambil penyederhanaan a = b = 1
solp:=eval(subs(a=1,b=1,solum)
sekarang kita memilih beberapa nilai untuk _Cl dan mengeplot solusi khusus yang
dihasilkan.
N1:=subs(_Cl=-0.5,solp);
N2:=subs(_Cl=0,solp);
N3:=subs(_Cl=0.5,solp);
N4:=subs(_Cl=2,solp);
N5:=subs(_Cl=8,solp);
Plot({rhs(N1), rhs(N2), rhs(N3), rhs(N4), rhs(N5)},t=0..5,title”Grefik Pertumbuhan
Verhulst”,axes=BOXED);
limit(N1,t=infinity);
limit(N2,t=infinity);
limit(N3,t=infinity);
limit(N4,t=infinity);
limit(N5,t=infinity);
17
Seperti yang tampak pada gambar, semua solusi mempunyai limit 1 tanpa
memperhatikan ukuran awal polulasi.
Contoh 8. persamaan diferensial Eksak.
Suatu persamaan diferensial orde pertama : M(x,y)dx + N(x,y) dy= 0
Dikatakan eksak jika ruas kiri persamaan ini merupakan diferensial total dari suatu
fungsi
U(x,y). Maka persamaan diferensial itu dapat dituliskan dengan du= 0.
Dengan pengintegralan, langsung kita peroleh solusi umum yang berbentuk
U(x,y)= c
Syarat perlu dan cukup agar persamaan diferensial
M(x,y)dx+N(x,y)=0
Merupakan persamaan difernsial eksak adalah
diff (M(x,y),y)=diff(N(x,y),x);
Fungsi u(x,y) dapat ditentukan dengan cara sebagai berikut;
Dari
diff(u(x,y),x)=M(x,y);diff(u(x,y),y)=N(x,y);
dengan mengintergralkan M(x,y) terhadap x dan y diperlukan sebagai konstan
diperoleh
u:=Int(M(x,y),x)+K(y);
dimana K(y) merupakan fungsi dari y saja dan berperanan sebagai suatu konstanta
integrasi.
Untuk menentukan K(y), kita menggunakan hubungan diff(u,y)=N(x,y);
Dengan mengintergralkan hasil ini terhadap y akan diperoleh K(y).
Pada contoh ini, kita akan menguji keeksakan sebuah persamaan difernsial dan
kemudian menyeleseikannya dam menggambar kurva solusinya. Pandang persamaan
diferansial
restart;
M :=y^2;
N : = 2*x*y;
M(y):=diff(M,y); N(x) := diff(N,x);
M(y) – N(x);
Dari persamaan difernsial itu adalah eksak Sekarang kita mendapatkan dua ekspresi
u1 dan u2 untuk u(x,y), yang satu melalui pengitegrasian M terhadap x, dan yang
lainnya melalui pengitergrasian N terhadap y.
u1 :int(y^2,x);
u2 =:int(2*x*y*,y);
Jadi solusi umum persamaan ini adalah
u(x,y) ;= x*y^2 =c;
up :=subs (c=2, u(x,y));
upl :=x*y^2-2;
18
Apabila kita menjumpai persamaan difernsial tidak eksak, kita dimungkinkan untuk
mereduksi persamaan diferensial tidak eksak menjadi persamaan diferensial eksak
dengan mengalikan persamaan itu dengan sebuah fungsi F(x,y) yang kemudian
dinamakan sebuah faktor integrasi. Jika sebuah persamaan mempunyai sebuah faktor
integrasi yang hanya bergantung pada salah satu dari dua variable (suatu sifat yang
harus didapaykan melalui percobaan), faktor ini dan solusi dari persamaan diferensial
eksek yang dihasilkan dapat diperoleh secara sistematrik Sebagai ilistrasi, perhatikan
contoh berikut:
Contoh 9. Solusi persamaan diferensial dengan faktor integrasi.
Pandang persamaan diferenial,
(2y-x^3)dx+x dy=0
Langkah pertama akan diuji keeksakannya.
restart;
M :=2*y-x^3;
N :=x;
diff(M,y)-diff(N,x);
Jadi persamaan ini tidak eksak. Kiti mencoba untuk faktor intergrasi yang hanya
bergantung pada x.
pers1:=diff(F(x)*M,y)-diff(Fx)*N,x)=0
do1 := dsolve(pers1, F(x);
u1 := int(rhs(so1)*M,x);
u2 := int(rhs(so1)*N,y);
Jadi solusi umum persamaan ini adalah
solum := x^2*y-1/58x^5=c;
Contoh 10. Pandang persamaan Diferensial
restart;
M := y-5*exp(-x)*cos(5*x);
N:=1;
diff(M,y)- diff(N,x);
Jadi persamaan ini tidak eksak. Kita mencoba mencari faktor intergrasi yang hanya
bergantung pada x.
persamaan:=diff(F(x)*M,y)-diff(F(x)*N,x)=0;
so1 := dsonlve(persam,F(x));
u1 :=(rhs(so1*M, x);
u2 :=int(rhs(so1)*N,y);
Jadi solusi umum bisa ditulis sebagai
solum :=y(x)=c*exp(x)*sin(5*x);
19
eval(subs(x=pi/10,y(pi/10)=exp(-pi/10),solum));
Jadi C=1.
1 :=subs(c=1,solum);
plot(rhs(p1),x=0..2*pi,title=”Gambar 1.8: grafik solusi y=exp(-x)sin5x”);
Contoh 11. masalah nilai awal.
restart’
N := csc(x);
M :=-(y*cot(x)*csc(x) + 20*cos(20*x));
diff (M,y)-diff(N,x);
Jadi persamaan ini merupakan persamaan diferensial eksak.
u1 :=int(M,x);
u2 :=int(N,y);
Jadi solusi umum persamaan ini adalah
solum :=y(x)=C*sin(x)+sin(x)*sin(20*x);
eval(subs(x+pi/2,y(pi/2)=0,solum));
Jadi solusi khusus masalah nilai awal ini adalah
yp :=subs(c=0, solum);
plot(rhs(yp),x=0...2*pi,title=”Gambar 1.9:Grafik solusi y=sin x sin 20x”);
Contoh 12. Rangkaian – RL.
Menurut hokum tegangan Kirchhoff, model rangkian –RL(rangkaian yang hanya
mengandung resistor dan kondukor) diberikan oleh persamaan diferensial diman
konstanta L dimankan indukstansi dari inductor yang diukur dalam henry, arus I
diukur dalam satuan ampere dan konstanta R dinamakan resistensi dari resistor yang
diukur dalam ohm,E(t) adalah beda tegangan pada waktu t yang diukur dlam atuan
volt.
Kasus a.Gaya elktromotif konstan yaitu bila E(t) + Eo+ konstanta. Persamaan itu
disajikan dalam bentuk persaman diferensial linier,
restart ;
p := R/L
r : = Eo/L;
h : = int(p,t);
Solusi umum persamaan ini adalah
solum := i(t0 = exp(=h)*(int(exp(h)*r,t) + c);
simplify(solum);
Jadi solusi umumnya berbentuk
i(t)= Eo/R + c*exp(-R/L*t);
Kita menuliskan I(t) dengan i(t) karena maple menyimpan I untuk akar dari –I.
20
Bila R =100 ohm,L=2,5 henry,Eo=100 volt dan I(O) =0 maka solusi khusus
persamaan ini adalah
eval9subs(t=0,i(0)=0,R=100,L=2,5,Eo=110, solum));
ip :=subs(R=100,L=2,5,Eo=110,c=-11/10,solum);
plot9rhs(ip),rhs(er)),t=0..0.2,title=”Gambar 1.10:Grafik solusi,kasus gaya elektromotif
konstan”);
Gambar 1.10 Grafik Solusi Kasus Gaya Elektromotif Konstan
limit(ip,t=infinity_;
Lim i(t)=100000000
Jadi fungsi Eo/R=11/10 merupakan fungsi keadan tetap atau penyelesaian keadaan
tetap.
Kasus b.Gaya elektromotif berkala.
E(t):=Eo*sin(omega*t);
p := R/L;
r := E(t)/L;
H :=int(p,t);
Solusi umum persamaan ini adalah
solum:= i(t) =exp(-H)*(int(exo(H)*r,t)+c);
solum:=i(t)=e
solum
:=i(t)=exp(-R*t/L)*(Eo*(omega*exp(R*t/L)*cos(omega*t)/(R^2)=omega^2)+R*t/L)*sin(omega*t)/(L*(R^2/(L
^2)+(L^2)+omega^2)))/L=c);
Solum :=i(t0=e
simplify(solum);
evalf(subs(t=0,i(0)=0,R=100,L=2,5,Eo=110,solum));
ip1 :=evalf(subs(c=44*(omega/1600+omega^2)),,R=100,L=2,5,Eo=110,solum));
plot3d(rhs(ip1),omega=0..1,
t=0..18,style=hidden,oriention=[-40,45],title=”Grafik
Solusi,kasus Gaya elektromotif berkala”,axes=BOXED);
RUMPUN KURVA. TRAYYEKTORI ORTHOGONAL
Pada bagian ini akan membuat Gambar rumpun kurva atau menggunakan persamaan
difernsial untuk menentukan kurva yang memotong kurva lain secara tegak lurus. Jika
untuk setiap nilai riil tertentu c berlaku persamaan
F(x,y,c)=0
Menggambarkan suatu kurva dalam bidang –xy dan jika untuk variable c hal ini
menggambarkan tak hingga banyaknya kurva, maka semua kurva ini dinamakan suatu
rumpun kurva satu parameter, dan c dinamakan parameter dari rumpun itu. Sebagai
contoh,persamaan:
F(x,y,c)=x^2+y^2-c^2=0
Menggambarkan suatu rumpun lingkaran sepusat dengan jari-jari c dan pusatnya di
titik asal (0,0).
Persamaan: 4y-x+c=0
21
Menggambarkan rumpun garis lurus parallel dengan kemiringan ¼.
Dalam beberapa penerapan, suatu kurva yang diberikan, diperlukan untuk menentukan
rumpun kurva yang lain yang memotong tegak lurus setiap kurva yang diberikan.
Pengertian tegak lurus disini adalah tegak lurus antara garis-garis singgung pada
kedua kurva yang berpotongan.maka kurva – kurva dari dua rumpun kurva ini dikatan
saling ortogonal dan merela membentuk jaringan orthogonal, dan rumpun kurva yang
diperoleh dinamakan trayektori orthogonal dari kurva yang diberikan (dan sebaliknya
). Diberikan rumpun kurva F(x,y,c)=0 yang dapat digambarkan oleh persamaan
diferensial
y’=f(x,y)
Kita dapat menentukan trayektori orthogonal yang bersesuaian.prosedur yang
digunakan adalah karena suatu kurva dari rumpun kurva yang diberikan tersebut yang
melalui titik (xo,yo) mempunyai kemiringan f(xo,yo) pada titik itu maka kemiringan
trayektori orthogonal yang melalui (xo,yo) pada titik ini akan berbanding terbalik
negative dengan f(xo,yo),yaitu -1/f(xo,yo),kerana hal ini merupakan syarat dari garis
singgung dari dua kurva yang berpotongan di (xo,yo) yang saling tegak lurus. Oleh
karena itu,persamaan difernsial dari trayektori ortogonalnya adalah:
y’=-1/f(x,y)
Solusi dari diferensial ini merupakan trayektori ortogonalnya.
Contoh 13.
Plot beberapa hiperbola xy=c konstan. Carilah dan plot beberapa trayektori
ortogonalnya.
Penyelesaiannya.
Dari kurva-kurva itu kita mendapatkan persamaan diferensialnya. Kita mengeplot
semua kurva dan trayektorinya sekaligus
restart;
Sebelum kita menggambarkan kurva – kurva dan trayektori orotgonalnya, kita akan
mengeplot dalam 3 dimensi dari fungsi f(x,y)=x y dengan perintah pot3d dan
kemudian mencoba untuk membuat sketsa diagram kontur dari grafik ini dengan
perintah contouplot.
with(plots);
f : =(x,y)-x*y;
plot3d(f(x,y),x=-2..2,y=-2..2,axes=BOXED,title=” Gambar 1.12: permukaan f(x,y)”);
contourplot(x,y),x=-2..2,y=2..2,axes=NORMAL,scaling=CONSTRAINED,title=”gambar
1.13:
Diagram
kontur dari f(x,y(=x y”);
pers1 :=x*y(x) = c; #kurva-kurva yang diketahui
pers2 := diff(pers1,x);#persamaan diferensial dari kurva-kurva itu.
f := solve(pers2, diff(y(x),x));#persamaan diferensial diseleseikan untuk y’
pers3 := diff(y(x),x) = -1/f; #persamaan diferensial dari trayektori.
tra := dsolve(pers3,y(x),explicit);#solusi dari persamaan diferensial
Jadi ada dua solusi. Kita dapat menemakan solusi pertama dengan tra[1] dan solusi
kedua degan tra[2].
C1 := 1/(4*x):#empat kurva yang akan diplot
22
C2 := 1/x:
C3 :=4/x:
C4 :=1/(2*x):
C4 := 9/x:
Sekarang kita mempersiapkan untuk mengeplot trayektori-trayektori tra[1]
K1 := subs(_C1 =0, tra[1];
K2 := subs(_C1 = 4, tra[1];
K3 := subs(_C1 = -4, tra[1];
K4:= subs(_ C1 = 8, tra[1];
K5 := subs(_C1 =-8, tra[1];
K5 := subs(_ C1 = 10, tra[1];
plot({c1,c2,c3,c4,c5,rhs(K1),rhs(K2),,rhs(K3),rhs(K4),rhs(K5),rhs(K6)},x=0..5,
y=0..5,title=”Gambar 1.14: Grafik Hiperbola xy=c dan Trayektori Ortogonalnya”);
2.1 Suatu persamaan difernsial orde kedua dikatakan linier jika persamaan itu dapat
dituliskan dalam bentuk
y”+p(x)y’+q(x)=r(x).
Ciri khas persamaan ini adalah linier dalam fungsi y yang tidak diketahui dan turunanturunannya,sedangkan p,q dan r dapat merupakan sembarangan fungsi dari x yang
diberikan. Fungsi p dan q itu dinamakan koefisien persamaan itu dan bila p dan q
keduanya berupa konstanta maka persamaan itu dinamakan persamaan difernsial orde
kedua dengan koefisien konstan. Jika r(x) =0 maka persamaan itu dikatakan homogen
dn jika tidak maka persamaan itu dikatakan tak homogen.sebagai contoh,persamaan
(2-x^2)y’-4x y’-6=x cos x
Merupakan persamaan difernsial linier tak homogen.
Suatu persamaan diferensial orde kedua yang tidak dapat dituliskan dalam bentuk di
atas dikatakan tak linier.Sebagai contoh,persamaan
yy”+xy+y=0
Merupakan persamaan difernsial tak linier.
Derivatif-deviratif y’,y” akan ditulis sebagai D(y)(x),(D@@2)(y)(x) atau
diff(y),x),diff(y(x),x,x). untuk mendapatkan nilai nol dari solusi denagn perintah solve
atau fsolve.Pengeplotan beberapa grafik solusi dengan perintah with(plots) diikuti
dengan perintah diplay.
2.2 contoh-contoh
Persamaan diferensial linier homogen koefisien konstan.
Contoh 1. Akar Ganda.
Kita akan menyeleseikan masalah nilai awal
y”+32,225y=0,y(0)=1,y’(0)=-2
Dan mengeplot kurva solusinya. Kemudian menghitung nilai maksimum atau
minimum dari solusi itu.
restart;
pers := (D@@2)(x) + 3*D(y)(x) =0;
yp := dsolve({pers,y(0) =1, D(y)(0) = -2}, y(x));
plot(rhs(yp), x=0.5..5, y= -0.1..1,title=”Gambar 2.1: Grafik solusi, Kasus akar
Ganda”);
23
Selanjutnya akan dicari nilai minimum dari yp.
tur1 :=diff(yp),x);
xk := solve(rhs(tur1) =0,x);#xk =x kritis
tru2 := diff(tru1,x);
ntru2 :=subs(x=8/3,rhs(tru2));#nilai turunan kedua di x kritis
Jadi yp mempunyai nilai minimum di x =8/3 yaitu
Ypmin := evalf(subs(x = xk,yp));
Contoh 2. Akar-akar riil berbeda.
Selesaikan masalah nilai awal
Prsm:=diff(y(x),x$2)+5*diff(y(x),x)+6*y(x)=0;
Solusi :=dsolve({prsm,t(0)=1.6,D(y)(0)=0},y(x));
Contoh 3. Akar-akar Kompleks.
Seleseikan masalah nilai awaly”+y’25,25y=0,y(0)=0,y’(0)=15.
Kemudian plotlah solusinya dan tentukan nilai maksimum atau minimum dari
solusinya.
Restart;
Pers := (D@@2)(y)(x) + D(y)+25,25*y(x)=0;
Plot(rhs(slop),x=0..2*pi,title=”Grafik solusi
Teredam)”);
Kasus
Akar
kompleks
(osilasi
Solusi osilasi ini merupakan bentuk khusus dari getaran teredam. Peredam mengambil
energi dari system,sehingga amplitude maksimum dariosi9lasi menurun menuju nol.
Selanjutnya akan dicari nilai maksimum dari solusinya.
Turn := diff(solp,x);
xm := solve(rhs(turn)=0,x);
xmax :=evalf(xmax);
ymax :=wvalf(subs(x = xmax, solp));
Contoh 4. berbagai konstanta peredam.
Untuk mengilustrasikan ketergantungan gerakan pada peredam,kita akan mencari dan
mengeplot lima solusi dari lima persamaan diferensial
Y” +cy’+900y = 0 dengan c =2 (oslasi besar),10,30,50,80.
Yang semuanya memnuhi y(0) = 1,y’(0)=0.
Restart;
Pers1 := (D@@2)(y)(x) + 2*D(y)(x) + 900*y(x)=0;
Pers2 := (D@@2)(y)(x) + 10*D(y)(x) + 1900*y(x)=0;
Pers3 := (D@@2)(y)(x) + 30*D(y)(x) + 900*y(x)=0;
Pers4 := (D@@2)(y)(x) +50*D(y)(x) +900*y(x)=0;
Pers5 := (D@@2)(y)(x) + 80*D(y)(x) + 900*y(x)=0;
Yp1 := dsolve({pers1,y(0)=1, D(y)(0)=0},y(x));
24
Yp2 := dsolve({pers2,y(0)=1,D(y)(0)=0},y(x));
Yp3 := dsolve({pers3,y(0)=1,D(y)(0)=0},y(x));
Yp4 := dsolve({pers4,y(0)=1,D(y)(0)=0},y(x));
Yp5:= dsolve({pers5,y(0)=1,D(y)(0)=0},y(x));
Plot({rhs(yp1),rhs(yp2),rhs(yp3),rhs(yp4),rhs(yp5)},x=0..0.9,title
Teredam dengan berbagai konstanta peredam”);
=”grafik
Osilasi
Plot menyajikan getaran –getaran bebas yang dimulai dari posisi awal sama dengan
kecepatan awal juga sama,untuk konstata-konstata peredam yang berbeda.sekarang
akan diselidiki perilku getaran bebas yang dimulai dari posisi awal yang sama dengan
kecepatan awal yang berbeda tetpi dengan konstanta peredam yang sama. Misalkan
persamaan getaran itu disajikan oleh:
4y”(t) + 24y’(t) + 36y(t)=0.
Dengan kondisi awal y(0)=1,y’(0)=0,1,10,-1,-10.
Pr :=4*(D@@2)(y)(t) +24*D(y)(t)+36y(t)=0;
Sol1 :=dsolve({pr,y(0)=1,D(y)(0)=0},y(t));
Sol2 :=dsolve({pr,y(0)=1,D(y)(0)=1},Y(t));
Sol3 :=dsolve({pr,y(0)=1,D(y)(0)=10},y(t));
Sol4 :=dsolve({pr,y(0)=1,D(y)(0)= -1},y(t)):
Sol5 :=dsolve({pr,y(0)=1,D(y)(0)= -10},y(t));
Plot({rhs(so1),rhs(slo2),rhs(sol3),rhs(sol4),rhs9sol5)},t=0..4,title=”Gerak
terdam kritis”);
bebas
Selnjutnya akan diselidiki perilakunya bila kita memperkecil konstanta peredam yaitu
dari 24 ke 6(osilasi kurang peredam(,yaitu dengan persamaan.
Per :4*(D@@2)(y)(t) +6*D(y)(t) +36*y(t)=0;
Sp1 :=dsolve({per,y(0)=1,D(y)(0)},y(t));
Sp2 :=dsolve({per,y(0)=1,D(y)(0)=1},y(t));
Sp3 ;=dsolve({per,y(0)=1,D(y)(0)=10},y(t));
Sp4 ;=dsolve({per,y(0)=1,D(y)(0)= -1},y(t));
Sp5 :=dsolve({per,y(0)=1,D(y)(0)= -10},y(t));
Plot({rhs(sp1),rhs(sp2),rhs(sp3),rhs(sp4),rhs(sp5)},t=0..7,title=”gerakOsilasiTeredam”
);
25