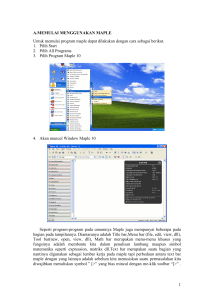
x=5^2+10*2+sqrt(9) - E

Praktikum IX Metode Numerik
PRAKTIKUM VIII
Materi : Sistem Persamaan Non Linear
Persamaan Non Linear
 persamaan yang pada saat digambar grafiknya bukan berupa garis lurus.
Cth persamaan non linear yang bentuknya teratur : polynomial.
Bentuk umum polynomial
P( s)  an s n  an 1s n 1  an  2 s n  2  ....  a1s  a0
Koefisien dari P(s) dapat real atau kompleks.
P(s) = 0
s: disebut akar-akar polynomial
Metode Bisection
Cari titik potong antara f1(x) dan f2(x) pada selang [x1,x2]
f1(x) = f2(x)
f1(x) - f2(x) = 0
f(x) = f1(x) - f2(x), f(x) = 0
f(x) ≈ 0
Tentukan x3 sebagai perkiraan penyelesaian dengan x3 = (x1+x2)/2
Cari nilai f(x1) dan nilai f(x3).
Jika f(x1).f(x3) < 0 ambil selang baru [x1,x3]
Jika f(x1).f(x3) ≥ 0 ambil selang baru [x3,x2]
Proses diulang sampai ditemukan penyelesaian
Metode False Position (Regula Falsi)
Menentukan x3 dari selang [x1, x2]
x f ( x 2 )  x 2 f ( x1 )
x3  1
f ( x 2 )  f ( x1 )
Sehingga selang baru yang digunakan adalah [x2,x3]
Instruksi-instruksi yang mungkin akan digunakan dalam praktikum kali ini :
tic dan toc
Digunakan untuk mengetahui waktu eksekusi suatu instruksi
tic;
Memulai perhitungan waktu (mereset timer).
a=toc;
Mengambil waktu proses (dari timer), disimpan ke dalam variable a. Waktu dihitung dari
dimulainya instruksi tic; Satuan: detik.
syms
Merupakan instruksi untuk membentuk objek symbolic (misalnya x), sehingga kita bisa
mengunakan operator aritmatik terhadap fungsi-fungsi matematis sebagaimana yang kita
lakukan terhadap bilangan.
collect
Mengumpulkan koefisien polynomial yang mempunyai derajat sama
Contoh Program 1:
syms x;
f1=input('Masukkan persamaan 1 = ');
f2=input('Masukkan persamaan 2 = ');
1
Praktikum IX Metode Numerik
2
f3=f1+f2;
hsl=collect(f3);
disp('f1 + f2 = ');
disp(hsl);
abs
Mencari nilai absolute/nilai mutlak
Cth:
y=abs(x);
diff
Merupakan instruksi untuk mencari turunan dari suatu fungsi.
diff(f) mencari turunan pertama.
diff(f,n) mencari turunan ke n.
subs
Fungsi yang digunakan untuk mengganti nilai x pada fungsi dengan nilai tertentu.
Contoh Program 2:
syms x;
f=input('Masukkan persamaan = ');
f1=diff(f);
t=5;
n=subs(f,x,t);
n1=subs(f1,x,t);
disp('Turunan pertama f = ');
disp(f1);
fprintf('Fungsi f dengan x diganti 5 = %d\n',n);
fprintf('Turunan f dengan x diganti 5 = %d\n',n);
Misal :
Kita punya fungsi :
f(x) = 2x3 + 3x + 10
f’(x) = 6x2 + 3
f(x=5) = 2.53 + 3.5 + 10 =275
f’(x=5) = 6.52 + 3 = 153
Dengan program diatas dapat kita lakukan dengan menjalankan program dan inputkan
persamaan sbb:
Masukkan persamaan = 2*x^3 + 3*x + 10
Turunan pertama f =
6*x2 + 3
Fungsi f dengan x diganti 5 = 275
Turunan f dengan x diganti 5 = 153
Contoh program 3:
%Akar persamaan kuadrat
clear;
a=input('Masukkan Nilai a = ');
b=input('Masukkan Nilai b = ');
c=input('Masukkan Nilai c = ');
tic;
d=b^2-(4*a*c);
if d>0
x1=(-b-d^0.5)/(2*a);
x2=(-b+d^0.5)/(2*a);
fprintf(' X1 =
%f \n',x1);
fprintf(' X2 =
%f \n',x2);
else if d==0
x=-b/(2*a);
fprintf(' X =
else
%f
\n',x);
Praktikum IX Metode Numerik
disp('Akar Kompleks');
end;
end;
w=toc;
fprintf('Waktu =
');
format long e;
disp([w]);
Langkah Kerja :
1. Cobalah contoh program 1,2 dan 3 diatas.
2. Implementasikan Metode Bisection
3. Implementasi metode Regula Falsi
3