Solusi Penyelesaian Gerak Parabola Mengg

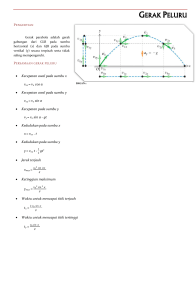
Laporan Praktikum Fisika Komputasi 1
(Solusi Penyelesaian Gerak Parabola Menggunakan Program C++)
Diajukan untuk memenuhi tugas mata kuliah Praktikum Fisika Komputasi 1
Disusun Oleh : Lida Maulida (1211703021)
Jurusan Fisika
Fakultas Sains dan Teknologi
Universitas Islam Negri Sunan Gunung Djati Bandung
2014
Daftar Isi
1
2
PENDAHULUAN
1
1.1
Latar Belakang . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
1
1.2
Tujuan . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
2
1.3
Rumusan Masalah . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
2
Tinjauan Pustaka
3
2.1
Metode Numerik . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
3
2.2
Gerak Dua Dimensi . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
4
2.2.1
2.3
Benda-benda yang melakukan gerakan peluru dipengaruhi oleh beberapa faktor: . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
4
2.2.2
Jenis-jenis gerak peluru: . . . . . . . . . . . . . . . . . . . . . . .
5
2.2.3
Menganalisis Gerak Peluru . . . . . . . . . . . . . . . . . . . . . .
6
Program C++ . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
7
DAFTAR PUSTAKA
9
ii
Bab 1
PENDAHULUAN
1.1
Latar Belakang
Secara garis besar, ilmu fisika dapat dipelajari lewat 3 jalan, yaitu pertama, dengan menggunakan konsep atau teori fisika yang akhirnya melahirkan fisika teori. Kedua, dengan cara
eksperimen yang menghasilkan aliran fisika eksperimental, dan ketiga, fisika bisa dipelajari lewat simulasi fenomena alam yang sangat mengandalkan komputer serta algoritma
numerik[1] .
Dalam bidang rekayasa, kebutuhan untuk menemukan solusi persoalan secara praktis adalah jelas. Dari kacamata rekayasawan, masih tampak banyak cara penyelesaian persoalan
matematik yang dirasa terlalu sulit atau dalam bentuk yang kurang kongkrit. Penyelesaian
analitik yang sering diberikan oleh kaum matematika kurang berguna bagi rekayasawan,
karena ia harus dapat mentransformasikan solusi matematika yang sejati ke dalam bentuk
berwudud yang biasanya meninggalkan kaidah kesejatiannya [BES97]. Solusi hampiran biasanya sudah memenuhi persyaratan rekayasa dan dapat diterima sebagai solusi. Lagipula,
banyak persoalan matematika dalam bidang rekayasa yang hanya dapat dipecahkan secara
hampiran. Kadang-kadang dapat pula terjadi bahwa metode analitik hanya menjamin keberadaan (atau hanya mengkarakteristikkan beberapa properti umum) solusi, tetapi tidak
memberikan cara menemukan solusi tersebut[KRE88].
Metode numeric digunakan untuk menyelesaikan persoalan dimana perhitungan secara analitik tidak dapat digunakan. Metode numeric ini berangkat dari pemikiran bahwa permasalahan dapat diselesaikan dengan menggunakan pendekatan-pendekatan yang dapat
1
1.2. Tujuan
2
dipertanggung-jawabkan secara analitik. Metode numerik ini disajikan dalam bentuk algoritmaalgoritma yang dapat dihitung secara cepat dan mudah.Pendekatan yang digunakan dalam
metode numerik merupakan pendekatan analisis matematis. Sehingga dasar pemikirannya
tidak keluar jauh dari dasar pemikiran analitis, hanya saja pemakaian grafis dan teknik perhitungan yang mudah merupakan pertimbangan dalam pemakaian metode numerik. Mengingat bahwa algoritma yangdikembangkan dalam metode numerik adalah algoritma pendekatan maka dalam algoritma tersebut akan muncul istilah iterasi yaitu pengulangan proses
perhitungan.Dengan kata lain perhitungan dalam metode numerik adalah perhitungan yang
dilakukan secara berulang-ulang untuk terus-menerus diperoleh hasil yang main mendekati
nilai penyelesaian exact.
1.2
Tujuan
Tujuan dari praktikum fisika komputasi I ini adalah dapat menyelesaikan solusi dari persamaan gerak dua dimensi khususnya untuk gerak peluru secara analitik dan menyelesaikan
dengan bahasa programan C++ secara sederhana.
1.3
Rumusan Masalah
1 . Bagaimana mencari solusi analitik untuk persamaan gerak peluru.
2 . Bagaimana mencari solusi numerik untuk persamaan gerak peluru dengan menggunakan program C++.
Lida Maulida (1211703021)
Solusi Gerak Parabola Menggunakan Program C++
Bab 2
Tinjauan Pustaka
2.1
Metode Numerik
Fisika komputasi adalah studi implementasi numerik algoritma untuk memecahkan masalah di bidang fisika di mana teori kuantitatif sudah ada [2] .Dalam sejarah, fisika komputasi
adalah aplikasi ilmu komputer modern pertama di bidang sains, dan sekarang menjadi subbagian dari sains komputasi.Dalam fisika, berbagai teori yang berdasarkan permodelan
matematika menyediakan prediksi yang akurat mengenai bagaimana sebuah sistem bergerak. Namun seringkali penggunaan permodelam matematika untuk sebuah sistem khusus
yang bertujuan untuk menghasilkan prediksi yang bermanfaat tidak bisa dilakukan ketika itu. Hal ini terjadi karena solusi permasalahan tidak memiliki ekspresi bentuk tertutup
(closed-form expression) atau terlalu rumit. Dalam banyak kasus, perkiraan numerik dibutuhkan. Fisika komputasi adalah subjek yang berhubungan dengan berbagai perkiraan
numerik; perkiraan solusi yang ditulis sebagai sejumlah besar bilangan terbatas (finite) dari
operasi matematika sederhana (algoritma), dan komputer digunakan untuk melakukan operasi tersebut dan menghitung solusi dan errornya.[2] .
Seperti telah dibahas di atas, metode numeric digunakan untuk menyelesaikan persoalan
dimana perhitungan secara analitik tidak dapat digunakan. Metode numeric ini berangkat
dari pemikiran bahwa permasalahan dapat diselesaikan dengan menggunakan pendekatanpendekatan yang dapat dipertanggung-jawabkan secara analitik. Metodenumerik ini disajikan dalam bentuk algoritma-algoritma yang dapat dihitung secara cepat dan mudah.
Pendekatan yang digunakan dalam metode numerik merupakan pendekatan analisis mate-
3
2.2. Gerak Dua Dimensi
4
matis. Sehingga dasar pemikirannya tidak keluar jauh dari dasar pemikiran analitis, hanya
saja pemakaian grafis dan teknik perhitungan yang mudah merupakan pertimbangan dalam
pemakaian metode numerik. Mengingat bahwa algoritma yangdikembangkan dalam metode numerik adalah algoritma pendekatan maka dalamalgoritma tersebut akan muncul istilah
iterasi yaitu pengulangan proses perhitungan. Dengan kata lain perhitungan dalam metode numerik adalah perhitungan yang dilakukansecara berulang-ulang untuk terus-menerus
diperoleh hasil yang main mendekati nilai penyelesaian exact[3] .
2.2
Gerak Dua Dimensi
Pada pokok bahasan Gerak Lurus, baik GLB, GLBB dan GJB, telah membahas gerak benda dalam satu dimensi, ditinjau dari perpindahan, kecepatan dan percepatan. Kali ini kita
mempelajari gerak dua dimensi di dekat permukaan bumi yang sering kita jumpai dalam
kehidupan sehari-hari. Contoh gerakan peluru/parabola yang kita jumpai dalam kehidupan sehari-hari. Diantaranya adalah gerak bola volly, gerakan bola basket, bola tenis,peluru
yang dtembakkan, gerakan lompat jauh yang dilakukan atlet dan sebagainya. Anda dapat
menambahkan sendiri. Apabila diamati secara saksama, benda-benda yang melakukan gerak peluru selalu memiliki lintasan berupa lengkungan dan seolah-olah dipanggil kembali
ke permukaan tanah (bumi) setelah mencapai titik tertinggi.
2.2.1
Benda-benda yang melakukan gerakan peluru dipengaruhi oleh beberapa faktor:
1. Benda tersebut bergerak karena ada gaya yang diberikan. Mengenai Gaya, selengkapnya kita pelajari pada pokok bahasan Dinamika (Dinamika adalah ilmu fisika yang
menjelaskan gaya sebagai penyebab gerakan benda dan membahas mengapa benda bergerak demikian). Pada kesempatan ini, belum menjelaskan bagaimana proses
benda-benda tersebut dilemparkan, ditendang dan sebagainya. Hanya memandang
gerakan benda tersebut setelah dilemparkan dan bergerak bebas di udara hanya dengan pengaruh gravitasi.
Lida Maulida (1211703021)
Solusi Gerak Parabola Menggunakan Program C++
2.2. Gerak Dua Dimensi
5
2. Benda-benda yang melakukan gerak peluru dipengaruhi oleh gravitasi, yang berarah
ke bawah (pusat bumi) dengan besar g = 9, 8m/s2 .
3. Hambatan atau gesekan udara. Setelah benda tersebut ditendang, dilempar, ditembakkan atau dengan kata lain benda tersebut diberikan kecepatan awal hingga bergerak, maka selanjutnya gerakannya bergantung pada gravitasi dan gesekan alias hambatan udara. Karena menggunakan model ideal, maka dalam menganalisis gerak peluru, gesekan udara diabaikan.
2.2.2
Jenis-jenis gerak peluru:
1. Benda meiliki kecepatan awal dan besar sudut tertentu pada arah horizontal. Seperti
gerakan bola villy, melempar bola, gerakan peluru atau rudal yang di tembakkan.
Gambar 2.1: Gerak Peluru (Melempar Bola)
2. Benda meiliki kecepatan awal pada ketinggian tertentu dengan arah sejajar horizontal.
Seperti gerakan bom yang dijatuhkan.
Gambar 2.2: Gerak Peluru (Bom Jatuh)
Lida Maulida (1211703021)
Solusi Gerak Parabola Menggunakan Program C++
2.2. Gerak Dua Dimensi
6
3. Benda meiliki kecepatan awal pada ketinggian tertentu dan memiliki besar sudut tertentu pada arah horizontal.
Gambar 2.3: Gerak Peluru (Lompatan Berenang)
2.2.3
Menganalisis Gerak Peluru
Gerak peluru adalah gerak dua dimensi, di mana melibatkan sumbu horisontal dan vertikal.
Jadi gerak parabola merupakan superposisi atau gabungan dari gerak horisontal dan vertikal. Kita sebut bidang gerak peluru sebagai bidang koordinat xy, dengan sumbu x horisontal
dan sumbu y vertikal. Percepatan gravitasi hanya bekerja pada arah vertikal, gravitasi tidak
mempengaruhi gerak benda pada arah horisontal.
Percepatan pada komponen x adalah nol (ingat bahwa gerak peluru hanya dipengaruhi oleh
gaya gravitasi. Pada arah horisontal atau komponen x, gravitasi tidak bekerja). Percepatan pada komponen y atau arah vertikal bernilai tetap (g = gravitasi) dan bernilai negatif
(−g) (percepatan gravitasi pada gerak vertikal bernilai negatif, karena arah gravitasi selalu
ke bawah alias ke pusat bumi). Kecepatan awal (V0 ) gerak benda diwakili oleh (V0x ) dan
Gambar 2.4: Gerak Peluru (Gerak Parabola)
(V0y ). (V0x ) merupakan kecepatan awal pada sumbu x, sedangkan (V0y ) merupakan keceLida Maulida (1211703021)
Solusi Gerak Parabola Menggunakan Program C++
2.3. Program C++
7
patan awal pada sumbu y. (Vy ) merupakan komponen kecepatan pada sumbu y dan (Vx )
merupakan komponen kecepatan pada sumbu x. Pada titik tertinggi lintasan gerak benda,
kecepatan pada arah vertikal (Vy ) sama dengan nol.
Maka kita dapat menuliskan persamaan gerak peluru secara lengkap sebagai berikut:
1. Persamaan gerak peluru pada sumbu x (Horizontal)
Vx = V0 Cosα
(2.1)
x = x0 + (V0 Cosα)t
(2.2)
2. Persamaan gerak peluru pada sumbu y (Vertikal)
2.3
Vy = V0 Sinα − gt
(2.3)
1
y = y0 + (V0 Sinα)t − gt2
2
(2.4)
Program C++
C++ adalah bahasa pemrograman komputer yang di buat oleh (Bjarne Stroustrup) merupakan perkembangan dari bahasa C dikembangkan di Bell Labs (Dennis Ritchie) pada awal
tahun 1970-an, Bahasa itu diturunkan dari bahasa sebelumnya, yaitu B, Pada awalnya, bahasa tersebut dirancang sebagai bahasa pemrograman yang dijalankan pada sistem Unix,
Pada perkembangannya, versi ANSI (American National Standart Institute) Bahasa pemrograman C menjadi versi dominan, Meskipun versi tersebut sekarang jarang dipakai dalam
pengembangan sistem dan jaringan maupun untuk sistem embedded, Bjarne Stroustrup pada Bel labs pertama kali mengembangkan C++ pada awal 1980-an. Untuk mendukung
fitur-fitur pada C++, dibangun efisiensi dan sistem support untuk pemrograman tingkat rendah (low level coding).[4] Pada C++ ditambahkan konsep-konsep baru seperti class dengan
Lida Maulida (1211703021)
Solusi Gerak Parabola Menggunakan Program C++
2.3. Program C++
8
sifat-sifatnya seperti inheritance dan overloading.[butuh rujukan] Salah satu perbedaan yang
paling mendasar dengan bahasa C adalah dukungan terhadap konsep pemrograman berorientasi objek (Object Oriented Programming).[5]
Perbedaan Antara Bahasa pemrograman C dan C++ meskipun bahasa-bahasa tersebut
menggunakan sintaks yang sama tetapi mereka memiliki perbedaan, C merupakan bahasa
pemrograman prosedural, dimana penyelesaian suatu masalah dilakukan dengan membagibagi masalah tersebut kedalam su-submasalah yang lebih kecil, Selain itu, C++ merupakan
bahasa pemrograman yang memiliki sifat Pemrograman berorientasi objek, Untuk menyelesaikan masalah, C++ melakukan langkah pertama dengan menjelaskan class-class yang
merupakan anak class yang dibuat sebelumnya sebagai abstraksi dari object-object fisik,
Class tersebut berisi keadaan object, anggota-anggotanya dan kemampuan dari objectnya,
Setelah beberapa Class dibuat kemudian masalah dipecahkan dengan Class.[6]
Lida Maulida (1211703021)
Solusi Gerak Parabola Menggunakan Program C++
Pustaka
9
Pustaka
[1] Suparno, Supriyanto. 2007. Komputasi Untuk Sains dan Teknik. FMIPA. Universitas
Indonesia.
[2] Thijssen, Joseph. 2007. Computational Physics; Cambridge University Press.
[3] https://www.academia.edu/4532357/Metode Numerik Sebagai Algoritma Komputasi.
(Diakses pada 30September 2014).
[4] Hanif al fatta .2006. Dasar Pemrograman C++ disertai dengan Pengenalan Pemrograman Berorientasi Objek. ISBN 979-763-582-1.
[5] Bruce Eckel (2000). Thinking in C++. Jilid 1 dari Thinking in C++ Introduction to
Standard C+, Bruce Eckel. ISBN 0139798099, 9780139798092.
[6] Bjarne Stroustrup .2000. The C++ programming language, Prentice Hall, 2000. ISBN
0201889544, 9780201889543.
[7] Pramuditya,S. 2007. Pengembangan Kode Komputer Terintegrasi untuk Studi Disain
Awal Pembangkit Listrik Tenaga nuklir Jenis PWR.
99
Lida Maulida (1211703021)
Solusi Gerak Parabola Menggunakan Program C++