TANTRI SATRIYA 16502050111016 - DISKRIMINAN, MANOVA, KANONIK

STATISTIK
A
MULTIVARI
AT
Analisa komponen utama,
analisa faktor, dan analisa
cluster
Tantri Satriya 165020501111016
Tantri Satriya 1650205011111016
ANALISA DISKRIMINAN
A. TEORI
Analisis diskriminan merupakan teknik multivariat yang termasuk
pada dependence method, dengan ciri adanya variabel dependen dan
independen. Ciri khusus analisis diskriminan adalah data variabel dependen
(Y) berupa data kategori sedangkan data untuk variabel independen (X)
berupa data numerik. Metode analisis diskriminan sendiri dibedakan
menjadi dua jenis, yaitu metode dengan dua kategori yang disebut dengan
Two-group Discriminant Analysis dan metode dengan lebih dua kategori
yang disebut dengan Multiple Discriminant Analysis. Analisa Diskriminan
memiliki beberapa kegunaan diantaranya : Mengetahui perbedaan yang
jelas antar grup pada variabel dependen, jika ada perbedaan, variabel
independen manakah pada fungsi diskriminan yang membuat perbedaan
tersebut, membuat fungsi atau model diskriminan, mengklasifikasikan
obyek ke dalam suatu kelompok atau kategori didasarkan pada nilai variabel
independen.
Model diskriminan memiliki dua jenis. Dua fungsi diskriminan yaitu
Fungsi Linier Fisher dan Fungsi Kuadratik. Fungsi diskriminan Linier
Fisher digunakan apabila asumsi normal multivariat dan asumsi
homogenitas matriks varian kovarian terpenuhi. Fungsi diskriminan
Kuadratik digunakan apabila asumsi normal multivariat terpenuhi tetapi
asumsi homogenitas matriks varian kovarian tidak terpenuhi. Fungsi linier
diskriminan linier fisher dapat dituliskan sebagai berikut :
𝐷 = 𝑏1𝑋1 + 𝑏2𝑋2 + ⋯ + 𝑏𝑝𝑋𝑝
dimana :
D : Skor diskriminan
b : Koefisien Diskriminan
X : Variabel Independen
Sementara Fungsi Diskriminan Kuadratik dapat dituliskan sebagai berikut :
2|STATISTIKA MULTIVARIAT
Tantri Satriya 1650205011111016
̂ 𝑄̇ (𝑥) = −
𝐷
𝐾
1
1
𝐼𝑛 |𝑆𝑘| − (𝑥 − 𝑋̅𝐾 )′ 𝑆𝑘−1 (𝑥 − ̅̅̅)
𝑥𝑘 + 𝐼𝑛𝑃𝑘
2
2
dimana :
̂ 𝑄̇ : skor diskriminan kelompok ke-k
𝐷
𝐾
|𝑆𝑘| : determinan matriks varian kovarian kelompok ke-k
𝑆𝑘−1 : invers matriks varian kovarian kelompok ke-k
𝑥
: vektor amatan
𝑥̅𝑘 : vektor rataan kelompok ke-k
𝑝
: prior probability
Fungsi diskriminan yang terbentuk sebanyak g –1 fungsi
diskriminan, dimana g adalah banyaknya kelompok atau kategori pada
variabel dependen (Y). Misalnya pada variabel Y terdapat 3 kategori maka
fungsi diskriminan yang terbentuk sebanyak 2 fungsi.
Seperti hal nya analisa statistic yang lain, analisa diskriminan
memiliki dua asumsi. Asumsi tersebut adalah asumsi normalitas dan
homegenitas. Multivariate normality. Variabel independen yang digunakan
dalam analisis diskriminan harus berdistribusi normal. Jika tidak normal
akan menyebabkan ketidaktepatan fungsi (model) diskriminan. Asumsi
selanjutnya adalah asumsi homogenitas matriks varian-kovarian. Asumsi ini
menguji apakah data yang digunakan bersifat homogen atau heterogen.
Fungsi dari asumsi normalitas adalah sebagai berikut
𝑓(𝑥):
1
1
𝐸𝑋𝑃
[−
(𝑥 − 𝜇)′𝜀 −1 (𝑥 − 𝜇)]
2
(2𝜋)𝑝/2 |𝜀|1/2
Hipotesis yang digunakan adalah:
H0 : variabel independen menyebar normal multivariat
H1 : variabel independen tidak menyebar normal multivariate
3|STATISTIKA MULTIVARIAT
Tantri Satriya 1650205011111016
Apabila nilai Sig. yang diperoleh > 0,05 maka menerima H0 sehingga dapat
disimpulkan bahwa asumsi normal multivariat terpenuhi
Asumsi selanjutnya adalah asumsi homogenitas matriks variankovarian. Fungsi dari asumsi ini adalah sebagai berikut :
𝐵𝑜𝑥 ′ 𝑠 𝑀 = −2 ln M
Dengan
𝑔
𝑔
𝑘=1
𝑘=1
1
1
𝐼𝑛 𝑀 = (∑(𝑛𝑘 − 1) 𝐼𝑛|𝑆𝑘| − ∑(𝑛𝑘 − 1) 𝐼𝑛|𝑆𝑔𝑎𝑏 |
2
2
𝑆𝑔𝑎𝑏 : matriks kombinasi varian-kovarian setiap kelompok
𝑆𝑘
: matriks varian-kovarian kelompok ke-k
Hipotesis yang digunakan adalah:
H0 : matriks varian kovarian bersifat homogen
H1 : matriks varian kovarian tidak bersifat homogeny
Apabila nilai signifikansi yang diperoleh lebih dari 0,05 maka terima H0
sehingga dapat disimpulkan bahwa data tersebut mempunyai matriks varian
kovarian yang homogen dan asumsi homogenitas matriks varian kovarian
terpenuhi.
Dalam menganalisis data dengan analisa diskriminan, ada beberapa
tahapan, diantaranya sebagai berikut :
a) Penentuan variabel independen yang menjadi pembeda terkuat dapat
dilihat dari nilai Wilk’s Lambda atau nilai F. Variabel independen
dikatakan variabel pembeda terkuat apabila memiliki nilai Wilk’s
Lambda terkecil atau nilai F terbesar dan mempunyai nilai Sig. < 0,05
b) Ketepatan fungsi klasifikasi, yang dapat dihitung dengan nilai Hit Ratio.
Nilai Hit Ratio lebih besar dari 50% dapat dikatakan bahwa fungsi
klasifikasi yang terbentuk baik. Rumus Hit Ratio adalah sebagai berikut
:
4|STATISTIKA MULTIVARIAT
Tantri Satriya 1650205011111016
𝐻𝑖𝑡 𝑅𝑎𝑡𝑖𝑜 =
𝑏𝑎𝑛𝑦𝑎𝑘𝑛𝑦𝑎 𝑑𝑎𝑡𝑎 𝑦𝑎𝑛𝑔 𝑡𝑒𝑝𝑎𝑡 𝑑𝑖𝑘𝑙𝑎𝑠𝑖𝑓𝑖𝑘𝑎𝑠𝑖𝑘𝑎𝑛
𝑏𝑎𝑛𝑦𝑎𝑘𝑛𝑦𝑎 𝑠𝑎𝑚𝑝𝑒𝑙
× 100
B. APLIKASI ANALISA DISKRIMINAN
1. Siapkan data
2. Masukkan data pada SPSS
5|STATISTIKA MULTIVARIAT
Tantri Satriya 1650205011111016
3. Beri Nama Variabel
4. Uji Normalitas
Pilih Analyze – Non Parametric test – Legacy Dialogs – 1 sample K.S
6|STATISTIKA MULTIVARIAT
Tantri Satriya 1650205011111016
5. Akan muncul kotak dialog One-Sample Kolmogorov... Masukkan
variabel independen ke kotak Test Variable List centang Normal pada
bagian Test Distribution kemudian klik Ok. Hasil pengujian normalitas
akan muncul pada output.
6. Masuk ke tahap pertama analisa diskriminan dengan cara pilih Analyze
– Classify – Discriminant
7|STATISTIKA MULTIVARIAT
Tantri Satriya 1650205011111016
7. Muncul kotak dialog Discriminant Analysis, masukkan variabel Y
pada Grouping Variable dan variabel X pada Independents kemudian
pada Grouping Variable pilih define range isikan minimum 1 dan
maximum 3 karena pada data yang digunakan kategori pada variabel Y
paling kecil yaitu 1 dan paling besar 3 kemudian klik continue
8. Pilih Statistic akan muncul kotak dialog Discriminant Analysis
Statistics centang pada bagian Univariate ANOVAs, Box’s M ,
Fisher’s dan Unstandardize kemudian klik continue
9. Pilih Classify akan muncul kotak dialog Discriminant Analysis
Classification centang Summary table pada bagian Display kemudian
klik continue
8|STATISTIKA MULTIVARIAT
Tantri Satriya 1650205011111016
10. Pilih Save akan muncul kotak dialog Discriminant Analysis Save
centang Predicted group membership kemudian klik continue
kemudian klik Ok hasil analisis diskriminan akan muncul pada output
11. Save Data
Pilih File – Save As Data
Pilih folder tempat menyimpan – Ketikkan nama file – klik save
9|STATISTIKA MULTIVARIAT
Tantri Satriya 1650205011111016
10 | S T A T I S T I K A M U L T I V A R I A T
Tantri Satriya 1650205011111016
C. INTERPRETASI
1. Uji Normalitas
Pada table tersebut nilai signifikansi > alfa, maka dapat dikatakan data
tersebar normal. Oleh karena itu, analisis dapat dilanjutkan.
2. Uji Box M
Uji Box’s M adalah pengujian untuk asumsi homogenitas matriks varian
kovarian. Berdasarkan output di samping diperoleh nilai Sig. Sebesar
0,104. Nilai tersebut lebih dari nilai alfa. Maka dapat disimpulkan
bahwa asumsi homogenitas matriks varian kovarian terpenuhi.
11 | S T A T I S T I K A M U L T I V A R I A T
Tantri Satriya 1650205011111016
3. Karena pada data ini terdapat 2 kategori pada variabel Y maka terbentuk
1 fungsi. Oleh karena itu, dilakukan pemilihan model/fungsi terbaik,
fungsi yang dipilih yaitu yang mempunyai eigenvalue > 1 dan Sig. dari
fungsi tersebut < 0,05
4. Wilks Lambda
Nilai signifikansi < alfa maka fungsi tersebut adalah fungsi yang baik
5. Canonical Discriminant Function Coefficiens
Output di samping menunjukkan fungsi diskriminan yang terbentuk.
Karena fungsi 1 yang terbaik maka fungsi diskriminan yang didapat
adalah:
D = 0.308X1 + 0.562X2 + 0.720X3 + 0.126X4
12 | S T A T I S T I K A M U L T I V A R I A T
Tantri Satriya 1650205011111016
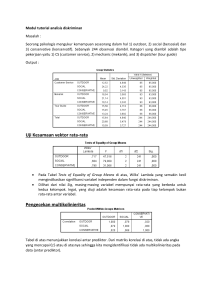
6. Test of Equality Group Means
Output di samping menunjukkan variabel mana yang berpengaruh dan
variabel mana yang menjadi pembeda terkuat. Variabel yang
berpengaruh yaitu X1, X2 x3, karena mempunyai nilai Sig. < 0,05 dan
variabel yang menjadi pembeda terkuat adalah variabel X1 dan X2
karena mempunyai nilai F terbesar.
7. Classification Results
Output di samping menunjukkan jumlah obyek yang tepat untuk
diklasifikasikan menggunakan analisis diskriminan. Obyek yang tepat
diklasifikasikan dapat dilihat pada diagonal utama
𝐻𝑖𝑡 𝑅𝑎𝑡𝑖𝑜 =
13 | S T A T I S T I K A M U L T I V A R I A T
49 + 43
× 100 = 92
100
Tantri Satriya 1650205011111016
ANALISA MANOVA
A. TEORI
MANOVA atau Multivariate Analysis of Variance merupakan
pengembangan dari ANOVA, yaitu sebagai metode statistik atau teknik
statistik yang digunakan untuk menghitung pengujian signifikansi perbedaan
rata-rata secara bersamaan antara kelompok untuk dua atau lebih variabel.
Karakteristik dari MANOVA adalah variabel independen bisa satu atau lebih
dari satu dan berupa data kategori sedangkan untuk variabel dependen harus
lebih dari satu dan berupa data kontinu. Perbedaan antara ANOVA dan
MANOVA didasari oleh banyaknya variable respon yang lebih dari satu. Jika
pada ANOVA, pengujian hipotesis nol adalah kesamaan rata-rata dari variable
predictor antar kelompok. Sedangkan, untuk MANOVA pengujian hipotesis
nol adalah kesamaan rata-rata dari vektor variabel respon antar kelompok.
Tujuan dari MANOVA yaitu untuk mengukur pengaruh variabel independen
terhadap beberapa variabel dependen secara simultan atau sekaligus.
INDIKATOR
BANYAKNYA VARIABEL PREDIKTOR
Banyaknya kel.
Satu Variat
Dua atau lebih
Data var respon
(Bivariat)
variat
(Multivariat)
Dua Kelompok
T tes
T2 Hotelling
Dua Atau lebih
ANOVA
MANOVA
kelompok
Ada dua model dalam Manova. Model-model tersebut ialah model
satu arah dan model dua arah. Model satu arah adalah sebagai berikut :
𝑋𝑖𝑗 = 𝜇 + 𝜏𝑖 + 𝜀𝑖𝑗
Sedangkan model dua arah adalah sebagai berikut :
𝑋𝑖𝑗𝑘 = 𝜇 + 𝜏𝑖 + 𝛾𝑘 + 𝜀𝑖𝑗𝑘
Hipotesa dalam Manova :
𝐻0: 𝜇1 = 𝜇12 = 𝜇1𝑘
= 𝜇2 = 𝜇22 = 𝜇2𝑘
= 𝜇𝑘 = 𝜇𝑘2 = 𝜇𝑘𝑙
14 | S T A T I S T I K A M U L T I V A R I A T
Tantri Satriya 1650205011111016
𝐻1 = 𝜇1 ≠ 𝜇12 ≠ 𝜇1𝑘
= 𝜇𝑘 ≠ 𝜇𝑘𝑙 ≠ 𝜇𝑘𝑙
Beberapa statistic uji yang dipakai dalam Manova adalah sebagai berikut :
1. Pillai’s Trace merupakan statistik uji yang digunakan apabila tidak
terpenuhinya asumsi homogenitas pada varians-kovarians, memiliki ukuran
sampel kecil dan jika hasil-hasil dari pengujian bertentangan satu sama lain
yaitu jika ada beberapa variabel dengan rata-rata yang berbeda sedang yang
lain tidak. Semakin tinggi nilai statistik Pillai’s Trace maka pengaruh terhadap
model akan semakin besar.
𝑘
𝑃𝑖𝑙𝑙𝑎𝑖 ′ 𝑠𝑇𝑟𝑎𝑐𝑒 = ∑
𝑖=1
𝛾𝑖
1 + λi
2. Wilk’s Lambda
Wilk’s Lambda merupakan 15tatistic uji yang digunakan apabila terdapat lebih
dari dua kelompok variabel 15tatistic15 asumsi homogenitas matriks varian
kovarian dipenuhi. Semakin rendah nlai 15tatistic Wilk’s Lambda, pengaruh
terhadap model semakin besar. Nilai Wilk’s Lambda berkisar antara 0 – 1.
𝑘
𝑊𝑖𝑙𝑘 ′ 𝑠𝑙𝑎𝑚𝑏𝑑𝑎 = ∏
𝑖=1
1
1 + λi
3. Hotelling’s Trace
Hotelling’s Trace merupakan 15tatistic uji yang digunakan apabila hanya
terdapat dua kelompok variabel respon. Semakin tinggi nilai 15tatistic
Hotelling’s Trace pengaruh terhadap model semakin besar.
𝑘
𝐻𝑜𝑡𝑒𝑙𝑙𝑖𝑛𝑔′ 𝑠𝑡𝑟𝑎𝑐𝑒 = ∑ λ𝑖
𝑖=1
4. Roy’s Largest Root
merupakan 15tatistic uji yang hanya digunakan apabila asumsi homogenitas
matriks varian kovarian dipenuhi. Semkin tinggi nilai 15tatistic Roy’s Largest
Root maka pengaruh terhadap model akan semakin besar.
15 | S T A T I S T I K A M U L T I V A R I A T
Tantri Satriya 1650205011111016
𝑅𝑜𝑦 ′ 𝑠 𝐿𝑎𝑟𝑔𝑒𝑠𝑡 =
λ𝑚𝑎𝑥
1 + 𝛾 𝑚𝑎𝑥
𝜆 merupakan eigenvalue
Dalam analisa Manova terdapat beberapa asumsi-asumsi ang harus
dipenuhi. Asumsi-asumsi tersebut adalah sebagai berikut :
a) Asumsi Homogenitas Ragam
Pengujian asumsi homogenitas berfungsi untuk mengetahui varians data
bersifat homogen atau heterogen. Uji ini bertujuan untuk melihat adanya
hubungan antar variabel respon. Hubungan antar variabel respon ditandai
dengan nilai matriks korelasi variabel respon tidak sama dengan matriks
identitas.
Uji homogen data dapat dilakukan melalui uji Bartlet dan Levene. Hipotesis
untuk uji ini adalah
H0 : R= 1 atau antar variabel memilik ragam sama
H1 : R = 1 atau antar variabel memiliki ragam tidak sama
Statistik uji yang digunakan adalah sebagai berikut :
2
𝑋𝐻𝑖𝑡𝑢𝑛𝑔
= − {𝑛 − 1 −
2𝑝 + 5
} 𝐼𝑛|𝑅|
6
Dimana p merupakan banyaknya variabel dan R matriks variabel Apabila
diperoleh nilai Sig. > 0,05 maka variabel tersebut memiliki ragam sama
sehingga asumsi homogenitas ragam terpenuhi.
b) Asumsi Normal Multivariat
Analisis data dengan menggunakan analisis multivariat harus memenuhi
asumsi berdistribusi normal multivariat, sehingga perlu dilakukan pengujian
distribusi normal multivariat. Variabel random (𝑥1, 𝑥2, 𝑥3, ..., 𝑥𝑝)
berdistribrusi normal dengan parameter 𝜇 dan Σ jika mempunyai Probability
density sebagai berikut :
16 | S T A T I S T I K A M U L T I V A R I A T
Tantri Satriya 1650205011111016
𝑓(𝑥) =
1
2
𝑝
(2𝜋)
𝑒𝑥𝑝−1/2[(𝑥−𝜇) ∑ −1(𝑥−𝜇)]
|𝜖|1/2
Pengujian hipotesis asumsi distribusi normal multivariat adalah sebagai
berikut H0 : data pengamatan berdistribusi normal multivariate
H1 : data pengamatan tidak berdistribusi normal multivariate
Apabila diperoleh nilai Sig. > 0,05 maka data pengamatan berdistribusi
normal multivariat sehingga asumsi normal multivariat terpenuhi.
17 | S T A T I S T I K A M U L T I V A R I A T
Tantri Satriya 1650205011111016
B. APLIKASI ANALISA MANOVA
1. Siapkan Data
2. Masukkan data pada SPSS
18 | S T A T I S T I K A M U L T I V A R I A T
Tantri Satriya 1650205011111016
3. Beri nama Variabel
4. Pada kolom Value klik pada “...” kemudian akan muncul kotak dialog.
Pada kolom value ini digunakan untuk mendefinisikan kategori pada
variabel X. 1 untuk Wire, 2 untuk Ball dan 3 untuk Mesin
19 | S T A T I S T I K A M U L T I V A R I A T
Tantri Satriya 1650205011111016
5. Langkah awal yaitu menguji asumsi normalitas multivariat. Pilih Analyze
– Descriptive Statistics – Explore
6. Muncul kotak dialog, masukkan variabel Y pada dependent list dan
variabel X pada factor list. Pilih Plots kemudian centang normality plots
with tests klik continue dan Ok
20 | S T A T I S T I K A M U L T I V A R I A T
Tantri Satriya 1650205011111016
7. Selanjutnya dilakukan analisis MANOVA. Pilih Analyze – Generaliz
Linear Model – Multivariate
8. Muncul kotak dialog, isikan variabel Y pada dependent variables dan
variabel X pada fixed factor(s)
21 | S T A T I S T I K A M U L T I V A R I A T
Tantri Satriya 1650205011111016
9. Pilih post hoc kemudian akan muncul kotak dialog masukkan variabel X
(metode) pada post hoc tests for dan centang LSD pada bagian equal
variance assumed.Setelah itu klik continue
10. Pilih option kemudian akan muncul kotak dialog masukkan overall pada
display means for dan centang observed power, homogenity test,
parameter estimates pada bagian Display.Setelah itu klik continue dan
klik Ok hasil analisis MANOVA muncul di output
22 | S T A T I S T I K A M U L T I V A R I A T
Tantri Satriya 1650205011111016
C. INTERPRETASI
1. Test Of Normality
Berdasarkan output di samping diperoleh bahwa nilai Sig. Uji Shapiro Wilk
> 0,05 maka dapat disimpulkan bahwa asumsi normalitas multivariat untuk
semua variabel telah terpenuhi
2. Lavense Test
Levene’s Test digunakan untuk menguji asumsi homogenitas ragam.
Berdasarkan output diperoleh bahwa nilai Sig. ball > 0,05 maka dapat
disimpulkan bahwa asumsi homogenitas ragam untuk ball telah terpenuhi
23 | S T A T I S T I K A M U L T I V A R I A T
Tantri Satriya 1650205011111016
3. Multuvariate Test
Output di atas untuk mengetahui apakah variabel independen berpengaruh
secara signifikan pada variabel dependen secara bersama. Berdasarkan
output di atas nilai Sig. Pada statistik uji MANOVA menunjukkan nilai <
0,05 hal ini berarti bahwa variabel independen (mesin) berpengaruh
terhadap variabel dependen (ball dan wire) secara bersama-sama
11. Tabel Test Of Between Subject Effects
Tabel diatas untuk mengetahui apakah variabel independen (metode)
berpengaruh secara signifikan terhadap masing-masing variabel
dependen. Berdasarkan output diperoleh bahwa nilai Sig. Yang diperoleh
pada masing-masing variabel dependen < 0,05 artinya adalah:
a. Mesin berpengaruh terhadap wire
b. Mesin berpengaruh pada ball
24 | S T A T I S T I K A M U L T I V A R I A T
Tantri Satriya 1650205011111016
12. Parameter Estimates
Tabel di atas untuk mengetahui variabel independen (Ball dan Wire) mana
yang berpengaruh secara signifikan terhadap masing-masing variabel
dependen (Mesin). Dikatakan berpengaruh apabila nilai Sig. Yang
diperoleh < 0,05 maka hasil yang diperoleh adalah:
a. Variabel Wire berpengaruh seara signifikan terhadap Mesin
b. Variabel Balls berpengaruh signifikan terhadap Mesin
25 | S T A T I S T I K A M U L T I V A R I A T
Tantri Satriya 1650205011111016
ANALISA KANONIK
A. TEORI
Analisis korelasi kanonik merupakan suatu teknik statistika
multivariat yang menyelidiki keeratan hubungan antara dua gugus variabel.
Gugus yang dimaksud adalah kelompok. Satu gugus variabel yang
diidentifikasikan sebagai gugus variabel independen (variabel X). Gugus
yang lain diidentifikasikan sebagai gugus variabel dependen (variabel Y).
Melalui ketergantungan antar kedua gugus variabel tersebut dapat
dijelaskan pengaruh dari satu gugus variabel terhadap gugus variabel yang
lainnya.
Dengan demikian, analisis korelasi kanonik adalah salah satu teknik
analisis statistik yang digunakan untuk melihat hubungan antara satu
kumppulan variabel independen dengan satu kumpulan variabel dependen.
Ada himpunan variabel (misal variabel X1 , X2 , X3 ,…, Xp ) ingin dilihat
keeratan hubungannya dengan himpunan variabel lain (Y1 , Y2 , Y3 , …,
Yq ) secara serempak / serentak / simultan analisis yang digunakan adalah
Analisis Korelasi Kanonik.
Terdapat dua jenis data dalam analisis korelasi kanonik, yaitu: 1)
Dua kelompok variabel yang diamati / diukur pada unit pengamatan sama
dalam waktu tertentu (bersamaan); 2) Satu himpunan variabel pada unit
observasi sama pada dua waktu. Ilustrasi untuk analisis korelasi kanonik
misalnya ingin mengetahui tingkat keeratan hubungan antara penggunaan
Facebook terhadap perilakunya. Maka gugus penggunaan facebook ini
terdiri dari beberapa variabel yaitu lama mengakses, aktivitas penggunaan
facebook, motivasi penggunaan facebook. Sedangkan gugus perilaku
terdiri dari perkembangan sosial siswa, prestasi belajar, lama jam belajar.
Seperti halnya pada analisa statistic yang lain, analisa korelasi
aknonik memiliki beberapa asumsi yang harus dipenuhi :
a) Asumsi Normal Multivariat
variabel dependen dan variabel independen yang akan
digunakan harus menyebar normal multivariat. Di mana fungsi
kepekatan normal multivariat adalah sebagai berikut:
26 | S T A T I S T I K A M U L T I V A R I A T
Tantri Satriya 1650205011111016
𝑓(𝑥) =
1
2
𝑝
(2𝜋) |𝜖|1/2
𝑒𝑥𝑝−1/2[(𝑥−𝜇) ∑ −1(𝑥−𝜇)]
Hipotesis yang digunakan adalah:
H0 : data menyebar normal multivariat
H1 : data tidak menyebar normal multivariat
Apabila nilai signifikansi yang diperoleh > 0,05 maka terima H0
dan dapat disimpulkan bahwa asumsi normal multivariat
terpenuhi
b) Asumsi Non Multikolinieritas, uji multikolinieritas adalah untuk
melihat ada atau tidaknya korelasi (keterkaitan) yang tinggi
antara variabel-variabel dalam suatu model. Pada analisis
korelasi kanonik diharapkan tidak ada multikolinieritas antar
anggota kelompok variabel, baik variabel independen maupun
variabel dependen.
Hipotesis yang digunakan yaitu:
H0 : tidak terjadi multikolinieritas
H1 : terjadi multikolinieritas
Apabila nilai signifikansi yang diperoleh > 0,05 maka terima H0
dan dapat disimpulkan bahwa asumsi non multikolinieritas
terpenuhi
Pada analisa Korelasi Kanonik, Fungsi kanonik yang terbentuk yaitu
minimum jumlah variabel dalam setiap kumpulan. Misalnya ingin mengetahui
keeratan kumpulan variabel X (ada 5variabel) dengan kumpulan variabel Y (ada 2
variabel) maka fungsi kanonik yang terbentuk sebanyak 2 fungsi. Penentuan fungsi
yang akan dipilih adalah berdasarkan tingkat signifikansinya. Ketika semua fungsi
signifikan dapat melihat korelasi kanoniknya, tidak ada ukuran yang pasti mengenai
seberapa besar hubungan yang harus terbentuk, faktor loading akan menjadi
alternatif dalam menentukan ukuran yang bermakan, faktor loading lebih besar dari
0,5
27 | S T A T I S T I K A M U L T I V A R I A T
Tantri Satriya 1650205011111016
Pada tahapan interpretasi kanonik akan didapatkan beberapa hasil :
a) Bobot kanonik (canonicalweight)
Bobot kanonik merupakan koefisien kanonik yang telah dibakukan, dapat
diinterpretasikan sebagai besarnya kontribusi peubah asalterhadap peubah
kanonik.Semakin besar nilai koefisien ini maka semakin besar kontribusi
peubah yang bersangkutan terhadap peubah kanonik.
b) Muatan kanonik (canonicalloadings)
Muatan kanonik dapat dihitung dari korelasi antara peubah asal
denganmasing-masing peubah kanoniknya.Semakin besar nilai muatan
kanonik maka akan semakin penting peran peubah asaltersebut
dalamkumpulan peubahnya.Peubah asal yang memiliki nilai muatan
kanonik > 0,5 akan dikatakan memiliki peran besar dan tanda muatan
kanonik menunjukkan arah hubungan
c) Muatan silang kanonik (canonical cross-loadings)
Muatan silang kanonik dapat dihitung dari korelasi antara peubah asal
dengan peubah kanonik pada kumpulan lainnya. Semakin besar nilai
muatan silang mencerminkan semakin dekat hubungan antara kedua
kumpulan. Peubah asal yang memiliki nilai muatan silang kanonik besar (
> 0,5 ) akan dikatakan memiliki peranan besar dalam kumpulan
peubahnya sedangkan tanda muatan silang kanonik menunjukkan arah
hubungannya
28 | S T A T I S T I K A M U L T I V A R I A T
Tantri Satriya 1650205011111016
B. APLIKASI ANALISA KORELASI KANONIK
1. Siapkan data
Data dibawah untuk melihat hubungan antara X1 : delivery speed X2 :
price level X3 : price flexibility X4 : manufacture image X5 : overall
service X6 : salesforce image X7 : product quality, dan Y1 :tingkat
penggunaan produk Y2 : kepuasan konsumen
2. Masukkan pada SPSS
29 | S T A T I S T I K A M U L T I V A R I A T
Tantri Satriya 1650205011111016
3. Beri label
4. Uji Asumsi Normalitas data
pilih Analyze – Nonparametric Test – Legacy Dialog - 1 sample K-S
30 | S T A T I S T I K A M U L T I V A R I A T
Tantri Satriya 1650205011111016
5. Muncul kotak dialog, masukkan semua variabel yang akan digunakan
ke test variable list kemudian centang Normal pada bagian test
distribution kemudian klik Ok . Setelah itu hasil akan keluar pada
output
6. Menguji asumsi non multikolinieritas
Pilih Analyze – Correlation – Bivariate
31 | S T A T I S T I K A M U L T I V A R I A T
Tantri Satriya 1650205011111016
7. Masukkan semua variabel ke dalam kotak variables. Centang Pearson,
pilih Two-tailed , dan centang flag significant correlations. Kemudian
klik Ok hasil akan keluar pada output
8. Analisis korelasi kanonik dilakukan pada Syntax SPSS, pilih File –
New – Syntax
32 | S T A T I S T I K A M U L T I V A R I A T
Tantri Satriya 1650205011111016
9. Tuliskan syntax di bawah ini pada bagian sebelah angka 1. syntax
yang dituliskan yaitu:
MANOVA Y1 Y2 WITH X1 X2 X3 X4 X5 X6 X7
/DISCRIM ALL ALPHA(1)
/PRINT=SIG(EIGEN DIM)
Y1 Y2 karena ada 2 variabel dependen yang digunakan dan X1 – X7
karena ada 7 variabel independen, kemudian klik tombol play
berwarna hijau setelah itu hasil akan keluar pada output
33 | S T A T I S T I K A M U L T I V A R I A T
Tantri Satriya 1650205011111016
C. INTERPRETASI
1. Uji Normalitas dengan Kolmogorv – Swirnov
Berdasarkan output di atas variabel yang telah memenuhi asumsi
normal multivariat adalah variable X1 dan X5, Y1 dan Y2.
untuk variabel yang lain masih belum memenuhi asumsi normal
multivariate. karena ini untuk pembelajaran maka proses analisistetap
dilanjutkan
2. Asumsi Multikoliniearitas
Berdasarkan output di samping
• Pada variabel independen masih ada beberapa nilai Sig. < 0,05
sehingga asumsi non multikolinieritas tidak terpenuhi
• Pada variabel dependen nilai Sig. < 0,05 maka disimpulkan asumsi
non multikolinieritas tidak terpenuhi.
Proses analisis korelasi kanonik tetap dilanjutkan untuk pembelajaran
walaupun asumsi tidak terpenuhi
34 | S T A T I S T I K A M U L T I V A R I A T
Tantri Satriya 1650205011111016
3. Eigenvalue
Pemilihan fungsi kanonik yang akan digunakan berdasarkan besar
keragaman yang diperoleh, output di atas menunjukkan besar
keragaman pada fungsi 1 sebesar 95,33% sedangkan fungsi kedua
relatif kecil besar keragamannya selain itueigenvalue yang diperoleh
lebih dari 1 sehingga fungsi kanonik 1 yang terpilih.
4. Dimension Reduction
Fungsi 1 dan fungsi 2 sama-sama memiliki nilai Sig. < 0,05 hal itu
berarti kedua fungsi tersebut siginifikan. Untuk interpretasi
selanjutnya digunakan fungsi 1 saja karena mempunyai besar
keragaman yang lebih besar dan eigenvalue yang diperoleh lebih
dari1.
5. Bobot Kanonik
35 | S T A T I S T I K A M U L T I V A R I A T
Tantri Satriya 1650205011111016
Bersasarkan Fungsi pertama dari bobot kanonik kontribusi terbesar
hingga terkecil adalah sebagai berikut :
1) Price flexibility(X3)
2) Overall service (X5)
3) Manufacture image (X4)
4) Delivery speed (X1)
5) Price level (X2)
6) Salesforce image (X6)
7) Product quality (X7)
8. Standarized Canonical Coefficient
Berdasarkan output bobot kanonik di atas, melihat pada fungsi 1
urutan kontribusi dari terbesar sampai terkecil terhadap peubah tak
bebas kanonik adalah 1) Tingkat penggunaan produk (Y1) 2)
Kepuasan konsumen (Y2)
9. Correllation between Covariates
Output di atas menunjukkan muatan kanonik peubah bebas. Melihat
pada fungsi pertama muatan kanonik peubah bebas yang mempunyai
korelasi paling kuat yaitu Overall Service (X5) dengan nilai korelasi
sebesar 0,76527
Corellation between Dependent and caonincal variabel
36 | S T A T I S T I K A M U L T I V A R I A T
Tantri Satriya 1650205011111016
Output di atas menunjukkan muatan kanonik peubah tak bebas.
Melihat pada fungsi pertama muatan kanonik peubah tak bebas yang
mempunyai korelasi paling kuat yaitu Y1
10. Raw Canonical for Covariates Function
Output di atas menunjukkan muatan silang kanonik peubah bebas.
Melihat pada fungsi pertama muatan silang kanonik peubah bebas
yang mempunyai korelasi paling kuat yaitu Overall Service (X5)
dengan nilai korelasi sebesar 0,59280
Output di atas menunjukkan muatan silang kanonik peubah tak bebas.
Melihat pada fungsi pertama muatan silang kanonik peubah tak bebas
yang mempunyai korelasi paling kuat adalah Y1
37 | S T A T I S T I K A M U L T I V A R I A T