Kalkulus2 Part2D

Ringkasan Kalkulus 2, Untuk dipakai di ITB
1
Limit dan Kekontinuan
Misalkan z = f (x, y) fungsi dua peubah dan (a, b) ∈ R2 . Seperti pada limit fungsi
satu peubah, limit fungsi dua peubah bertujuan untuk mengamati kecendrungan nilai
f (x, y) bila (x, y) mendekati titik (a, b).
x2 −y 2
x2 +y 2
di bawah ini.
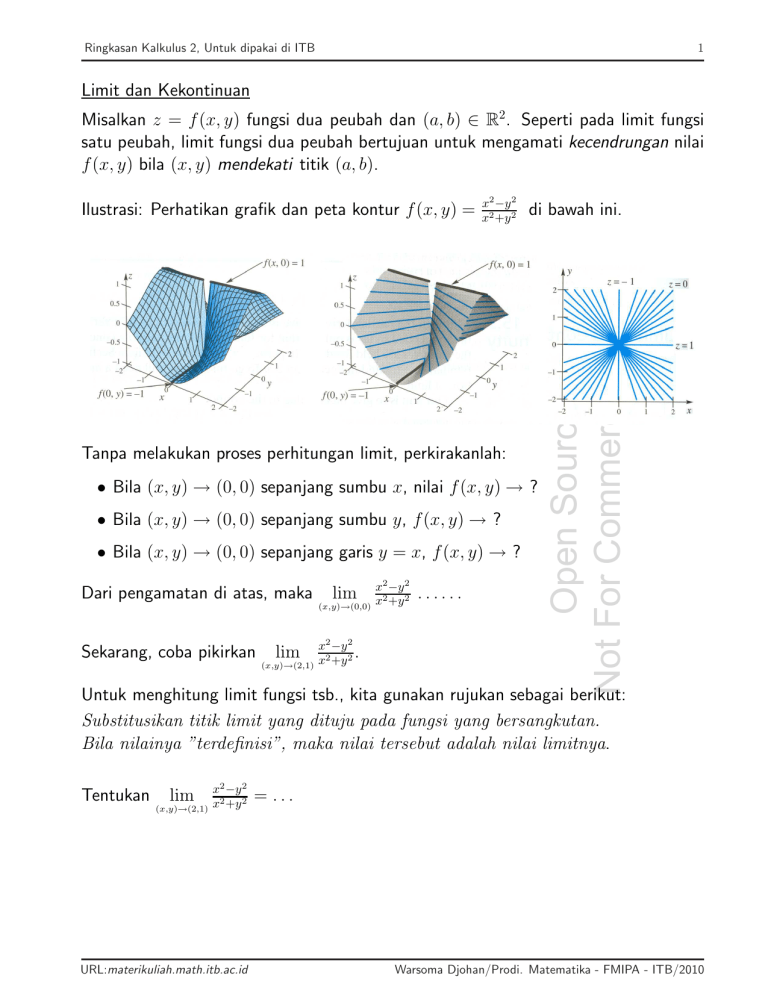
Tanpa melakukan proses perhitungan limit, perkirakanlah:
• Bila (x, y) → (0, 0) sepanjang sumbu x, nilai f (x, y) → ?
• Bila (x, y) → (0, 0) sepanjang sumbu y, f (x, y) → ?
• Bila (x, y) → (0, 0) sepanjang garis y = x, f (x, y) → ?
Dari pengamatan di atas, maka
Sekarang, coba pikirkan
lim
(x,y)→(2,1)
lim
(x,y)→(0,0)
x2 −y 2
.
x2 +y 2
x2 −y 2
x2 +y 2
......
Open Source
Not For Commercial Use
Ilustrasi: Perhatikan grafik dan peta kontur f (x, y) =
Untuk menghitung limit fungsi tsb., kita gunakan rujukan sebagai berikut:
Substitusikan titik limit yang dituju pada fungsi yang bersangkutan.
Bila nilainya ”terdefinisi”, maka nilai tersebut adalah nilai limitnya.
Tentukan
lim
(x,y)→(2,1)
x2 −y 2
x2 +y 2
URL:materikuliah.math.itb.ac.id
= ...
Warsoma Djohan/Prodi. Matematika - FMIPA - ITB/2010
Ringkasan Kalkulus 2, Untuk dipakai di ITB
2
Definisi Limit Fungsi 2 Peubah
Limit dari fungsi dua peubah f (x, y) untuk
(x, y) mendekati (a, b) disebut L, ditulis
lim f (x, y) = L artinya untuk setiap
(x,y)→(a,b)
Catatan:
• Fungsi f (x, y) tidak perlu terdefinisi pada titik
(a, b).
• Nilai limit f (x, y) tidak boleh bergantung pada
arah (x, y) mendekati (a, b).
(Pada fungsi dua peubah tidak ada istilah limit
kiri atau limit kanan).
Contoh2:
1. Tunjukan
2. Tunjukan
lim
(x,y)→(0,0)
x2 −y 2
x2 +y 2
tidak ada.
lim
x2 y
x4 +y 2
tidak ada.
(x,y)→(0,0)
Open Source
Not For Commercial Use
ǫ > 0, selalu dapat dicari δ > 0 sehingga
0 < |(x, y) − (a, b)| < δ ⇒ |f (x, y) − L < ǫ.
p
Catatan: |(x, y) − (a, b)| = (x − a)2 + (y − b)2
(Petunjuk: Hitung sepanjang garis y = mx dan parabola y = x2)
URL:materikuliah.math.itb.ac.id
Warsoma Djohan/Prodi. Matematika - FMIPA - ITB/2010
Ringkasan Kalkulus 2, Untuk dipakai di ITB
3
Kekontinuan di satu titik
Fungsi f (x, y) disebut kontinu di (a, b) bila memenuhi
lim
(x,y)→(a,b)
= f (a, b)
Sifat2:
• Bila f (x, y) dan g(x, y) kontinu di (a, b) maka f + g, f − g, f g dan f /g kontinu
di (a, b).
• Polinom dua peubah, p(x, y) = a + bx + cy + dx2 + exy + f y 2 + · · · kontinu di
R2
Open Source
Not For Commercial Use
• fungsi rasional dua peubah kontinu di seluruh daerah definisinya.
• Fungsi komposisi. Misalkan g(x, y) kontinu di (a, b) dan f (x) kontinu di g(a, b),
maka f ◦ g(x, y) = f (g(x, y)) kontinu di (a, b).
Contoh: Jelaskan kekontinuan fungsi f (x, y) = cos(x3 − 4xy + y 2 ).
Kekontinuan di himpunan
Misalkan S ⊂ R2 . Fungsi dua peubah f (x, y) disebut kontinu
pada S bila f kontinu pada setiap titik pada S. Perlu diperhatikan bila S memiliki batas (perhatikan gambar di samping
ini), maka proses limit hanya dilakukan sepanjang jalur yang
berada dalam S saja.
Sifat:
Misalkan f (x, y) fungsi dua peubah. Bila fxy dan fy x kontinu pada himpunan buka
S, maka fxy = fyx pada S.
URL:materikuliah.math.itb.ac.id
Warsoma Djohan/Prodi. Matematika - FMIPA - ITB/2010
Ringkasan Kalkulus 2, Untuk dipakai di ITB
4
Keterdiferensialan
Perkuliahan ini tidak akan membahas konsep diferensial fungsi dua peubah secara
teoritik. Pembahasan konsep akan langsung dianalogikan dengan konsep turunan di
fungsi satu peubah.
Perhatikan fungsi satu peubah f (x), p ∈ Df dan h ∈ R. Bila fungsi tersebut mempunyai turunan, maka berlaku f (p + h) = f (p) + f ′ (p)h + ǫ(h2 )
∇f (~p) = hfx (~p), fy (~p)i = fx (~p)î + fy (~p)ĵ
Open Source
Not For Commercial Use
Untuk fungsi dua peubah hal yang analog berlaku. Misalkan f (x, y) fungsi dua peubah
dan p = (x, y) ∈ Df . Untuk memudahkan notasi, kita akan menuliskan p sebagai
vektor ~p = hx, yi. Pada fungsi dua peubah berlaku hubungan f (~p + ~h) = f (~p) +
∇f (~p) · ~h + ǫ(h2 ) dengan,
Catatan: Vektor ∇f dibaca grad dari f dan disebut vektor gradien dari fungsi dua
peubah f (x, y).
Sifat: Bila fx (x, y) dan fy (x, y) kontinu di lingkungan sekitar (a, b) maka f (x, y)
terdiferensialkan di (a, b) dengan gradien ∇f (a, b).
Contoh: Tunjukan f (x, y) = xey + x2y terdiferensialkan di mana-mana dan tentukan
gradiennya.
Sifat2 ∇:
a. ∇[f (~p) + g(~p)] = ∇f (~p) + ∇g(~p)
b. ∇[αf (~p)] = α ∇f (~p)
c. ∇[f (~p) g(~p)] = ∇f (~p) g(~p) + f (~p) ∇g(~p)
Sifat:
Jika fungsi f (x, y) terdiferensial pada p~ maka f (x, y) kontinu di ~p.
URL:materikuliah.math.itb.ac.id
Warsoma Djohan/Prodi. Matematika - FMIPA - ITB/2010
Ringkasan Kalkulus 2, Untuk dipakai di ITB
5
Turunan berarah
Popon berada pada sebuah keping dengan distribusi
suhu seperti pada gambar di samping.
a. Bila dia bergerak pada arah horizontal, berapakah
laju perubahan suhunya ?
Open Source
Not For Commercial Use
b. Pada arah manakah dia harus bergerak supaya
penurunan suhunya maksimum?
Pertanyaan (a) sudah dapat anda jawab yaitu · · · · · ·.
Untuk menjawab pertanyaan (b), kita akan mempelajari konsep turunan berarah. Misalkan f (x, y) fungsi dua peubah dan ~p = hx, yi ∈ Df .
f (~p + h î) − f (~p)
h→0
h
fx(~p) = lim
dan
f (~p + h ĵ) − f (~p)
h→0
h
fy (~p) = lim
Misalkan ~u vektor satuan pada bidang,
~u = hu1 , u2i = u1 î + u2 ĵ. Turunan berarah dari f (x, y)
pada arah ~u di titik p adalah:
D~uf (~p) =
∂f
f (~p + h ~u) − f (~p)
(~p) = lim
h→0
∂~u
h
Perhatikan: fx(~p) = Dî f (~p) dan fy (~p) = Djˆf (~p)
Secara fisis, turunan berarah menyatakan laju perubahan f (x, y) di titik ~p bila f
begerak pada arah ~u.
Secara umum, menghitung D~u f (~p) dari konsep limit di atas cukup menyulitkan. Biasanya perhitungan dilakukan melalui sifat berikut:
Misalkan f (x, y) terdiderensialkan di p~, maka D~u f (~p) = ~u · ∇f (~p)
Contoh: Misalkan f (x, y) = 4x2 − xy + 3y 2 , tentukan turunan berarah dari f di titik
(2, −1) : (a.) pada arah ~a = h4, 3i.
(b.) pada arah menuju titik (5, 3).
Diskusi: Misalkan z = f (x, y), pada arah manakah D~u f (~p) naik dan turun paling
cepat ?
URL:materikuliah.math.itb.ac.id
Warsoma Djohan/Prodi. Matematika - FMIPA - ITB/2010
Ringkasan Kalkulus 2, Untuk dipakai di ITB
6
Contoh: Seekor kutu berada pada titik (2,-1,21) di permukaan f (x, y) = 4x2 − xy +
3y 2 , tentukan pada arah mana dia harus bergerak agar tanjakannya maksimum dan
berapa tanjakan tersebut ?
Perhatikan kurva ketinggian L dari z = f (x, y) yang melalui
titik P (x0, y0). Misalkan ~u vektor singgung satuan terhadap
L di titik P . D~u f (p) = 0 (mengapa ?). Dilain pihak
D~u f (p) = ~u · ∇f (p). Dengan demikian ∇f (p) ⊥ ~u atau
∇f (p) ⊥ L di titik P .
2
Open Source
Not For Commercial Use
Kurva Ketinggian vs Gradien
Contoh: Diberikan fungsi z = x4 + y 2 . Tentukan vektor gradien yang melalui titik
(2, 1), lalu gambarkan kurva ketinggian yang melalui titik tersebut dan vektor gradiennya.
Aturan Rantai Jenis 1
Misalkan z = f (x, y), dengan x = x(t) dan y = y(t).
Di sini f merupakan fungsi dua peubah terhadap x dan
y, tetapi terhadap t merupakan fungsi satu peubah.
Aturan rantai memberikan formula untuk menghitung
turunan f terhadap t:
∂z dx ∂z dy
dz
=
+
dt
∂x dt ∂y dt
Contoh: Misalkan z = x3y dengan x = 2t dan y = t2 . Tntukan
dz
dt .
Aturan Rantai Jenis 2
Misalkan z = f (x, y), dengan x = x(s, t) dan y = y(s, t). Di sini f merupakan fungsi
dua peubah terhadap x dan y, juga fungsi dua peubah terhadap s dan t. Aturan
rantai memberikan formula untuk menghitung turunan parsial f terhadap s dan t:
∂z ∂x ∂z ∂y
∂z
=
+
∂s ∂x ∂s ∂y ∂s
dan
∂z
∂z ∂x ∂z ∂y
=
+
∂t
∂x ∂t ∂y ∂t
Contoh: Misalkan z = x3y dengan x = 2s + 7t dan y = 5st.
∂z
Tentukan ∂z
∂s dan ∂t .
URL:materikuliah.math.itb.ac.id
Warsoma Djohan/Prodi. Matematika - FMIPA - ITB/2010
Ringkasan Kalkulus 2, Untuk dipakai di ITB
7
Penurunan Fungsi Implisit dengan aturan Rantai
a. Untuk fungsi satu peubah
Misalkan F (x, y) = 0 mendefinisikan y sebagai fungsi x secara implisit. Turunkan
dx
∂F dy
kedua ruas terhadap x, maka diperoleh: ∂F
∂x dx + ∂y dx = 0.
∂F /∂x
dy
=−
dx
∂F /∂y
Turunkan terhadap y, diperoleh:
Karena
∂x
∂y
= 0 dan
∂F /∂x
∂z
=−
∂x
∂F /∂z
∂y
∂x
∂F ∂x
∂x ∂y
+
∂F ∂y
∂y ∂y
+
∂F ∂z
∂z ∂y
= 0 (mengapa ?), maka
dan
∂z
∂F /∂y
=−
∂y
∂F /∂z
Contoh:
Open Source
Not For Commercial Use
b. Untuk fungsi dua peubah
Misalkan F (x, y, z) = 0 mendefinisikan z sebagai fungsi x dan y secara implisit.
∂y
∂x
∂z
Turunkan terhadap x, diperoleh: ∂F
+ ∂F
+ ∂F
= 0.
∂x ∂x
∂y ∂x
∂z ∂x
= 0.
dy
dari x3 + x2y − 10y 4 = 0
1. Tentukan dx
(gunakan dua cara: aturan rantai dan penurunan implisit).
2. Tentukan
∂z
∂x
dan
∂z
∂y
URL:materikuliah.math.itb.ac.id
dari x3 ey+z − y sin(x − z) = 0
Warsoma Djohan/Prodi. Matematika - FMIPA - ITB/2010
Ringkasan Kalkulus 2, Untuk dipakai di ITB
8
Bidang Singgung
Perhatikan permukaan F (x, y, z) = 0 dan V bidang
singgung di titik p = (x0, y0, z0 ).
∇F (p) = hFx (p), Fy (p), Fz (p)i ⊥ V (?).
Misalkan (x, y, z) sebarang titik pada bidang V .
Jelas ∇F (p) ⊥ hx − x0 , y − y0, z − z0 i (?).
∇F (p) · hx − x0, y − y0, z − z0 i = 0.
hFx(p), Fy (p), Fz (p)i · hx − x0 , y − y0, z − z0 i = 0
Fx(p)(x − x0) + Fy (p)(y − y0 ), Fz (p)(z − z0 ) = 0
Open Source
Not For Commercial Use
Dengan demikian setiap titik pada bidang singgung memenuhi persamaan:
Hal khusus, bila z = f x, y).
Tulis f (x, y) − z = 0 = F (x, y, z).
∇F = hfx , fy , −1i.
Dengan demikian persamaan garis singgung terhadap
f (x, y) di titik p adalah
fx(p)(x − x0) + fy (y − y0) − (z − z0 ) = 0
Contoh:
1. Tentukan persamaan garis singgung terhadap x2 + y 2 + 2z 2 = 23 di titik (1, 2, 3).
2. Tentukan persamaan garis singgung terhadap z = x2 + y 2 di titik (1, 1, 2).
3. Tentukan persamaan garis singgung yang sejajar dengan bidang xoy terhadap
z = x2 − 2xy − y 2 − 8x + 4y.
URL:materikuliah.math.itb.ac.id
Warsoma Djohan/Prodi. Matematika - FMIPA - ITB/2010
Ringkasan Kalkulus 2, Untuk dipakai di ITB
9
Diferensial dan Aproksimasi
Misalkan fungsi z = f (x, y).
(x0, y0 , z0) & (x, y, z) ∈ Df .
Diferensial dari peubah bebas x
dan y adalah:
dx = ∆x = x − x0
dy = ∆y = y − y0
Open Source
Not For Commercial Use
tetapi,
∆z = z − z0 = f (x, y) − f (x0, y0)
dan diferensial dari peubah tak bebas z adalah
dz = fx(x0, y0)dx + fy (x0, y0 )dy.
Interpretasi geometri dari ∆z dan dz diperlihatkan pada gambar di atas.
Untuk dx dan dy yang cukup kecil ∆z ≈ dz. Diperoleh rumus aproksimasi
∆z = f (x, y, z) − f (x0, y0 , z0) ≈ fx(x0, y0)dx + fy (x0, y0)dy = dz
Contoh2:
1. Misalkan z = 2x3 + xy − y 3 . Tentukan ∆z dan dz bila (x, y) berubah dari (2, 1)
ke (2, 03 ; 0, 98).
√
2. Gunakan hampiran diferensial untuk menghitung 3,9 · 9,1.
URL:materikuliah.math.itb.ac.id
Warsoma Djohan/Prodi. Matematika - FMIPA - ITB/2010
Ringkasan Kalkulus 2, Untuk dipakai di ITB
10
Maksimum dan Minimum Fungsi 2 Peubah
Misalkan z = f (x, y) dan p0 ∈ Df
a. f disebut mencapai maksimum di p0 bila
f (p0) ≥ f (p) ∀ p ∈ Df , nilai maksimumnya f (p0).
c. f disebut mencapai maksimum lokal di p0 bila
f (p0) ≥ f (p) untuk semua titik p disekitar p0.
d. f disebut mencapai minimum lokal di p0 bila
f (p0) ≤ f (p) untuk semua titik p disekitar p0.
Titik tempat terjadinya maksimum/minimum global/lokal
disebut titik ekstrim.
Titik ekstrem tidak selalu ada (berikan contoh).
Bila daerah definisi dari f (x, y) berupa himpunan tertutup dan terbatas, maka titik ekstrim global selalu ada.
Open Source
Not For Commercial Use
b. f disebut mencapai minimum di p0 bila
f (p0) ≤ f (p) ∀ p ∈ Df , nilai minimumnya f (p0).
(Teorema titik kritis). Titik ekstrim selalu merupakan salah satu dari:
a. Titik stasioner, yaitu titik yang memenuhi hubungan ∇F = 0
b. Titik singular, yaitu titik yang turunannya tidak ada.
c. Titik batas dari Df



T itik

 kritis
2
Contoh: Tentukan titik ekstrim lokal dari f (x, y) = x2 − 2x + y4 .
fx(x, y) = 2x − 2 dan fy (x, y) = y2 . Titik stasioner (1, 0) dan f (1, 0) = −1.
Titik singular dan titik batas tidak ada. Perhatikan bahwa:
2
2
2
f (x, y) = x2 − 2x + y4 = x2 − 2x + 1 + y4 − 1 = (x − 1)2 + y4 − 1 ≥ −1
Jadi (1, 0) merupakan titik minimum global, dan tidak ada titik maksimum.
Teorema Pengujian titik ekstrim lokal
Misalkan f (x, y) mempunyai turunan parsial kedua yang kontinu disekitar titik sta2
sioner p0 = (x0, y0 ). tetapkan D = fxx (p0) fyy (p0) − fxy
(p0),
a.
b.
c.
d.
Jika
Jika
Jika
Jika
D > 0 dan fxx (p0) < 0, maka p0 titik maksimum lokal.
D > 0 dan fxx (p0) > 0, maka p0 titik minimum lokal.
D < 0, maka p0 titik pelana (bukan titik ekstrim).
D = 0, tidak ada kesimpulan.
URL:materikuliah.math.itb.ac.id
Warsoma Djohan/Prodi. Matematika - FMIPA - ITB/2010
Ringkasan Kalkulus 2, Untuk dipakai di ITB
11
Latihan
1. Tentukan titik ekstrim lokal dan titik pelana dari z =
−x2
a2
+
y2
b2 .
2. Tentukan titik pada z 2 = x2y + 4 yang jaraknya paling dekat ke titik asal.
Open Source
Not For Commercial Use
3. Tentukan titik ekstrim dari f (x, y) = 2 + x2 + y 2 pada daerah
2
S = {(x, y) : x2 + y4 ≤ 1}
(petunjuk: untuk mencari titik ekstrim pada batas S, gunakan substitusi
x = cos t dan y = 2 sin t dengan · · · ≤ t ≤ · · ·).
URL:materikuliah.math.itb.ac.id
Warsoma Djohan/Prodi. Matematika - FMIPA - ITB/2010
Ringkasan Kalkulus 2, Untuk dipakai di ITB
12
Ekstrim dengan Kendala, Metode Lagrange
Masalah titik ekstrim pada fungsi 2 peubah ada dua macam:
a. Masalah ekstrim bebas (yang telah dibahas pada pasal sebelumnya).
b. Masalah ekstrim dengan kendala/syarat
Masalah ekstrim dengan kendala membahas masalah mencari titik ekstrim sepanjang kurva z = f (x, y) dengan syarat titik-titik (x, y) berada sepanjang lengkunagn
g(x, y) = 0. Sebagai contoh, perhatikan ilustrasi berikut:
2
Open Source
Not For Commercial Use
Carilah nilai maksimum dari f (x, y) = 2+x2 +y 2 sepanjang g(x, y) = x2 + y4 −1 = 0.
Dengan mesubstitusikan kurva kendala pada f (x, y) akan diperoleh masalah ekstrim
bebas (dengan jumlah peubah bebas yang lebih sedikit), selanjutnya dapat diselesaikan
dengan metode pencarian ekstrim bebas. Namun demikian, tidak selalu kurva kendala
dapat disubstitusikan ke dalam fungsi semula (cari contohnya).
Metode Pelipat Lagrange merupakan alternatif lain untuk mencari ekstrim dengan
kendala. Perhatikan kurva ketinggian dari
f (x, y) = k untuk k = 200, 300, · · · , 700
yang digambarkan bersama-sama dengan
kendala g(x, y) = 0.
Yang harus ditentukan adalah titik pada kurva ketinggian dengan nilai k terbesar yang
juga dilalui kendala g(x, y) = 0 (mengapa demikian ?).
URL:materikuliah.math.itb.ac.id
Warsoma Djohan/Prodi. Matematika - FMIPA - ITB/2010
Ringkasan Kalkulus 2, Untuk dipakai di ITB
13
Titik tersebut terletak pada kurva ketinggian yang bersinggungan dengan g(x, y) = 0.
Pada ilustrasi, titik tersebut adalah p0 dengan nilai k = 600. ∇f (p0) ⊥ kurva ketinggian f (x, y) = 600 dan ∇g(p0) ⊥ g(x, y) = 0 (mengapa ?). Karena f (x, y) = 600
dan g(x, y) = 0 bersinggungan di p0 maka ∇f (p0) segaris dengan ∇g(p0). Jadi di
titik maksimum diperoleh hubungan ∇f (p0) = λ∇g(p0 ) dengan λ suatu bilangan real.
Hal yang sama juga berlaku di titik minimum (titik p1).
∇f (x, y) = λ∇g(x, y)
dan
g(x, y) = 0
Open Source
Not For Commercial Use
Dengan demikian diperoleh kesimpulan sebagai berikut: (Metode Lagrange)
Untuk mencari titik ekstrim dari z = f (x, y) dengan kendala g(x, y) = 0, carilah
solusi dari sistem persamaan
Titik-titik p yang memenuhi persamaan tersebut merupakan titik kritis dari masalah
ekstrim terkendala. Bilangan λ disebut pelipat Lagrange.
Diskusi:
1. Bila didapatkan n buah titik kritis, bagaimanakah menentukan titik maksimum
dan minimumnya ?
2. Bila didapatkan 1 buah titik kritis, bagaimanakah menentukan titik maksimum
dan minimumnya ?
Contoh2:
2
1. Carilah nilai maksimum dari f (x, y) = 2+x2 +y 2 sepanjang g(x, y) = x2 + y4 −1 =
0.
2. Carilah titik-titik ekstrim dari f (x, y) = y 2 − x2 pada elips
x2
4
+ y 2 = 1.
3. Tentukan volume maksimum dari sebuah kotak yang dapat dibuat bila harga bahan
alasnya tiga kali harga bahan sisi yang lain. Harga bahan alasnya Rp 6.000/m2 dan
jumlah uang yang tersedia Rp. 120.000. (Catatan: ∇f (x, y, z) = hfx, fy , fz i).
4. Tentukan titik ekstrim dari f (x, y, z) = x + 2y + 3z pada elips yang merupakan
perpotongan silinder x2 + y 2 = 2 dengan bidang y + z = 1.
Catatan: Masalah ini adalah masalah ekstrim dengan dua kendala yaitu g(x, y, z) =
0 dan h(x, y, z) = 0, rumus metode Lagrange-nya adalah:

 ∇f (x, y, z) = λ∇g(x, y, z) + µ∇h(x, y, z)
g(x, y, z) = 0

h(x, y, z) = 0
URL:materikuliah.math.itb.ac.id
Warsoma Djohan/Prodi. Matematika - FMIPA - ITB/2010