Silabus Sekolah : Mata Pelajaran : Matematika Kelas/Program : XI

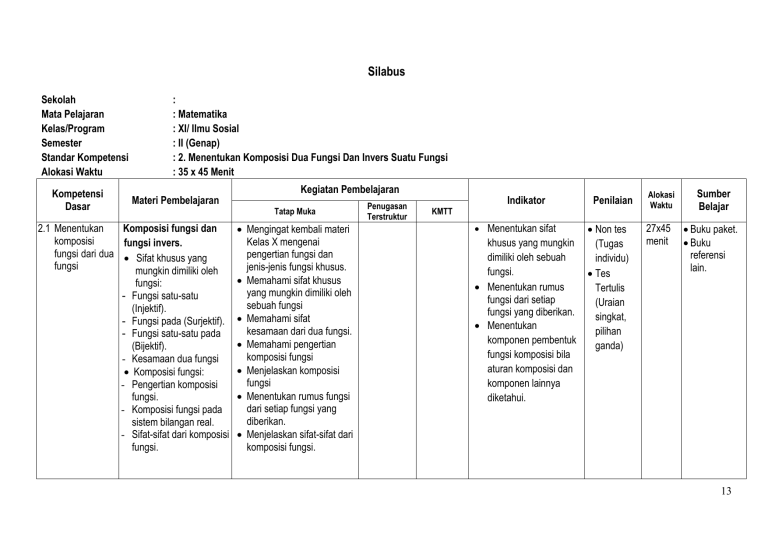
Silabus
Sekolah
Mata Pelajaran
Kelas/Program
Semester
Standar Kompetensi
Alokasi Waktu
Kompetensi
Dasar
:
: Matematika
: XI/ Ilmu Sosial
: II (Genap)
: 2. Menentukan Komposisi Dua Fungsi Dan Invers Suatu Fungsi
: 35 x 45 Menit
Materi Pembelajaran
2.1 Menentukan
Komposisi fungsi dan
komposisi
fungsi invers.
fungsi dari dua  Sifat khusus yang
fungsi
mungkin dimiliki oleh
fungsi:
- Fungsi satu-satu
(Injektif).
- Fungsi pada (Surjektif).
- Fungsi satu-satu pada
(Bijektif).
- Kesamaan dua fungsi
 Komposisi fungsi:
- Pengertian komposisi
fungsi.
- Komposisi fungsi pada
sistem bilangan real.
- Sifat-sifat dari komposisi
fungsi.
Kegiatan Pembelajaran
Tatap Muka
 Mengingat kembali materi
Kelas X mengenai
pengertian fungsi dan
jenis-jenis fungsi khusus.
 Memahami sifat khusus
yang mungkin dimiliki oleh
sebuah fungsi
 Memahami sifat
kesamaan dari dua fungsi.
 Memahami pengertian
komposisi fungsi
 Menjelaskan komposisi
fungsi
 Menentukan rumus fungsi
dari setiap fungsi yang
diberikan.
 Menjelaskan sifat-sifat dari
komposisi fungsi.
Penugasan
Terstruktur
KMTT
Indikator
 Menentukan sifat
khusus yang mungkin
dimiliki oleh sebuah
fungsi.
 Menentukan rumus
fungsi dari setiap
fungsi yang diberikan.
 Menentukan
komponen pembentuk
fungsi komposisi bila
aturan komposisi dan
komponen lainnya
diketahui.
Penilaian
 Non tes
(Tugas
individu)
 Tes
Tertulis
(Uraian
singkat,
pilihan
ganda)
Alokasi
Waktu
27x45
menit
Sumber
Belajar
 Buku paket.
 Buku
referensi
lain.
13
Kompetensi
Dasar
Materi Pembelajaran
 Fungsi Invers:
- Pengertian invers
2.2 Menentukan
fungsi.
invers suatu
- Menentukan rumus
fungsi.
fungsi invers.
- Grafik suatu fungsi
dan grafik fungsi
inversnya.
 Fungsi invers dari
fungsi komposisi
Kegiatan Pembelajaran
Tatap Muka
 Memahami pengertian
dari invers suatu fungsi.
 Menjelaskan syarat suatu
fungsi mempunyai invers.
 Menentukan apakah suatu
fungsi mempunyai invers
atau tidak.
 Menentukan rumus fungsi
invers dari fungsi yang
diketahui dan sebaliknya.
 Menggambarkan grafik
fungsi invers dari grafik
fungsi asalnya.
 Menentukan daerah asal
fungsi inversnya.
 Membahas teorema yang
berkenaan dengan fungsi
invers.
 Menentukan rumus
komposisi fungsi dari dua
fungsi yang diberikan.
 Menentukan rumus dan
nilai fungsi invers dari
fungsi kompisisi.
Penugasan
Terstruktur
KMTT
Indikator
 Menentukan rumus
fungsi invers dari suatu
fungsi.
 Menggambarkan grafik
fungsi invers dari grafik
fungsi asalnya.
Penilaian
Alokasi
Waktu
8x45
menit
Sumber
Belajar
 Buku paket.
 Buku
referensi
lain.
 Menentukan fungsi
invers dari fungsi
komposisi dan nilainya.
14
Standar Kompetensi
Alokasi Waktu
Kompetensi
Dasar
1.1 Menghitung
limit
fungsi
aljabar
sederhana di
suatu titik
1.2 Menggunakan
sifat limit
fungsi untuk
menghitung
bentuk tak
tentu fungsi
aljabar.
: 3. Menggunakan Konsep Limit Fungsi dan Turunan Fungsi dalam Pemecahan Masalah.
: 50 x 45 Menit
Materi Pembelajaran
Limit fungsi
 Limit fungsi aljabar:
- Definisi limit secara
intiutif.
- Definisi limit secara
aljabar.
- Limit fungsi-fungsi
f  x
berbentuk xlim
c
(cara substitusi,
faktorisasi, dan
perkalian sekawan).
- Limit fungsi di tak
hingga
 Penggunaan limit
 Limit fungsi aljabar
 Penggunaan limit


Kegiatan Pembelajaran
Tatap Muka
 Menjelaskan arti limit fungsi
secara intiutif dan
aljabarberdasarkan fungsi
aljabar yang sederhana.
 Menghitung limit fungsi
aljabar di suatu titik
menggunakan cara substitusi,
faktorisasi, dan perkalian
dengan sekawan.
 Menghitung limit fungsi
aljabar di tak hingga .
 Menjelaskan penggunaan
limit dalam mencari garis
singgung suatu kurva di suatu
titik tertentu.
 Menggunakan limit dalam
menentukan laju perubahan
suatu fungsi pertumbuhan.
Turunan fungsi:
Definisi turunan fungsi.
Notasi turunan.
Teorema-teorema
 Memahami definisi turunan
1.3 Menggunakan
umum turunan fungsi
fungsi.
sifat dan aturan  Persamaan garis
 Menghitung turunan fungsi
turunan dalam
singgung di suatu titik
dengan menggunakan definisi
perhitungan
pada kurva.
turunan.
turunan fungsi
 Menjelaskan arti fisis dan
aljabar.
geometri turunan fungsi di
Penugasan
Terstruktur
KMTT
Indikator
 Menghitung limit
fungsi aljabar di
suatu titik dan tak
hingga.
 Menggunakan
limit dalam
mencari garis
singgung suatu
kurva dan laju
perubahan suatu
fungsi.
 Menghitung
turunan fungsi
dengan
menggunakan
Penilaian
 Non tes
(Tugas
individu)
 Tes
Tertulis
(Uraian
singkat,
pilihan
ganda)
Alokasi
Waktu
Sumber
Belajar
10x45  Buku paket.
menit  Buku
referensi
lain.
10x45  Buku paket.
menit  Buku
referensi
lain.
 Buku paket.
14x45  Buku
menit
referensi
lain.
15
Kompetensi
Dasar
Kegiatan Pembelajaran
Materi Pembelajaran
Tatap Muka








1.4 Menggunakan
turunan untuk
menentukan
karakteristik
suatu fungsi
dan
memecahkan
suatu titik.
Menentukan turunan suatu
fungsi di satu titik tertentu..
Menjelaskan dan menentukan
laju perubahan nilai fungsi.
Memahami notasi turunan
fungsi.
Menggunakan notasi turunan
dalam menentukan laju
perubahan nilai fungsi.
Menjelaskan teorema-teorema
umum turunan fungsi.
Menggunakan teoremateorema turunan fungsi untuk
menghitung turunan fungsi
aljabar.
Membuktikan teoremateorema umum turunan fungsi.
Mengingat kembali materi
mengenai arti fisis dan
geometri dari turunan fungsi di
suatu titik.
Menentukan gradien dari
suatu kurva di suatu titik.
Membahas cara menentukan
persamaan garis singgung
pada suatu kurva di suatu titik.
 Fungsi naik dan fungsi

turun
 Sketsa grafik dengan

uji turunan.
- Mensketsa grafik
dengan uji turunan
pertama.
 Memahami definisi fungsi naik
- Mensketsa grafik
dan fungsi turun.
Penugasan
Terstruktur
KMTT
Indikator
Penilaian
Alokasi
Waktu
Sumber
Belajar
definisi turunan.
 Menentukan
turunan suatu
fungsi di satu titik
tertentu.
 Menentukan laju
perubahan nilai
fungsi terhadap
variabel bebasnya.
 Menentukan
turunan fungsi
aljabar.
 Buku paket.
12x45  Buku
menit
referensi
lain.
 Menentukan
16
Kompetensi
Dasar
masalah.
1.5 Merancang
model
matematika
dari masalah
yang
berkaitan
dengan
ekstrim fungsi
aljabar.
Materi Pembelajaran
dengan uji turunan
kedua.
 Pergerakan.
- Kecepatan.
- Percepatan
 Masalah maksimum
dan minimum.
- Masalah maksimum
dan minimum jika
fungsinya diketahui.
- Masalah maksimum
dan minimum jika
fungsinya tidak
diketahui.
Kegiatan Pembelajaran
Tatap Muka
 Menentukan selang interval
dimana fungsi naik dan turun.
 Mensketsa grafik dengan uji
turunan pertama dengan
menentukan titik stasionernya.
 Mensketsa grafik dengan uji
turunan kedua dan
menentukan jenis titik
ekstrimnya
 Memahami pengertian dari
kecepatan dan percepatan.
 Menghitung kecepatan dan
dan percepatan dengan
menggunakan turunan.
 Mengingat kembali materi
mengenai cara menghitung
turunan fungsi.
 Menyelesaikan masalah
maksimum dan minimum jika
fungsinya diketahui.
 Menafsirkan solusi dari
masalah yang diperoleh.
 Menjelaskan karakteristik
masalah dimana fungsinya
tidak diketahui yang akan
dicari maksimum atau
minimumnya.
Penugasan
Terstruktur
KMTT
Indikator
Penilaian
Alokasi
Waktu
Sumber
Belajar
persamaan garis
singgung pada
suatu kurva.
 Menentukan selang
dimana fungsi naik
atau turun.
 Menentukan titik
stasioner suatu
fungsi beserta
jenis ekstrimnya.
 Mensketsa grafik
fungsinya.
4x45
menit
 Buku paket.
 Buku
referensi
lain.
 Menggunakan
turunan dalam
perhitungan
kecepatan dan
percepatan.
17
Kompetensi
Dasar
1.6 enyelesaikan
model
matematika
dari masalah
yang
berkaitan
dengan
ekstrim fungsi
aljabar dan
penafsirannya
.
Mengetahui
Kepala SMA
Nip.
Materi Pembelajaran
Kegiatan Pembelajaran
Tatap Muka
 Menentukan besaran masalah
yang akan dijadikan sebagai
variabel dalam ekspresi
matematikanya.
 Merumuskan fungsi satu
variabel yang merupakan
model matematika dari
masalah.
 Menentukan penyelesaian
dari model matematika
tersebut.
 Memberikan tafsiran terhadap
solusi dari masalah dimana
fungsinya tidak diketahui.
Penugasan
Terstruktur
KMTT
Indikator
Penilaian
Alokasi
Waktu
Sumber
Belajar
 Menentukan
penyelesaian dari
model matematika
yang berkaitan
masalah
maksimum dan
minimum
2011
Guru Mata Pelajaran
Nip.
18